
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как формируются силы, определяющие величину скорости звенаи направление его движения.Содержание книги
Поиск на нашем сайте
Скорости и ускорения ведомых звеньев механизма могут быть определены методами планов, кинематических диаграмм и аналитическими. Во всех случаях в качестве исходных должны быть известны: схема механизма при определенном положении ведущего звена, его скорость и ускорение. Метод планов. Построение планов скоростей и ускорений проводится на основе последовательного составления векторных уравнений для всех групп, входящих в механизм, начиная с ведущего звена. Для определения полной картины скоростей любого звена, входящего в группу, достаточно знать линейные скорости двух точек этого звена или линейную скорость одной точки и угловую скорость звена. Так как скорости конечных элементов звеньев групп известны, то необходимо выбрать общую для двух звеньев точку и записать два уравнения для определения скорости этой точки. Для групп первого, второго и четвертого видов это постоянная точка — центр средней вращательной пары группы, для других — мгновенная точка на одном звене, совпадающая в данный момент с центром конечной вращательной пары другого звена.
В качестве примера рассмотрим построение планов скоростей и ускорений группы второго класса второго вида. План скоростей. В этой группе (рис. 2.3, а) полагаем, что скорости примыкающих звеньев 1 и 4 заданы. Следовательно, скорость точки В2, принадлежащей звену 2, равна скорости точки Blt принадлежащей звену 1, т. е.
Рассмотрим движение звена 2 относительно звена 1. Эти звенья образуют вращательную пару, поэтому на основании теоремы о сложении скоростей в сложном движении скорость точки С на звене 2 складывается из скорости
где vCB = Теперь определим скорость точки С, отнеся ее к третьему звену. Звено 3 образует со звеном 4 поступательную пару, поэтому скорость точки С3 можно представить как сумму двух скоростей: скорости Vc4 точки С4, совпадающей с точкой С3 и принадлежащей среде переноса (в данном случае примыкающему звену 4), и скорости точки С3 относительно точки С4 в поступательном движении I звена 3 относительно звена 4 — Vc3c4, т. е.
Точку С4 расположим на плоскости, жестко связанной со звеном 4. Зная закон движения этого звена, можно найти мгновенный центр вращения (МЦВ) и при известных расстоянии его от точки С4 и угловой скорости ω4 определить величину и направление скорости этой точки.
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.01 с.) |

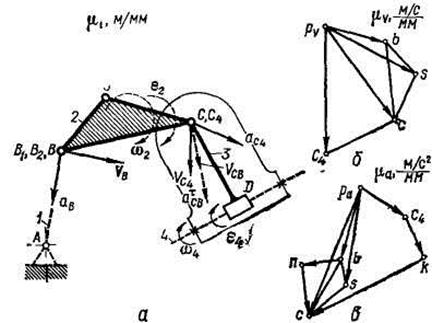 При составлении векторных уравнений следует четко установить точки, скорости которых используются как скорости в переносном движении. Если звенья группы образуют поступательные кинематические пары, то необходимо использовать точки, принадлежащие направляющим звеньям.
При составлении векторных уравнений следует четко установить точки, скорости которых используются как скорости в переносном движении. Если звенья группы образуют поступательные кинематические пары, то необходимо использовать точки, принадлежащие направляющим звеньям.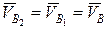 . Угловая скорость звена 3, образующего поступательную пару со звеном 4, равна заданной угловой скорости звена 4, т. е.
. Угловая скорость звена 3, образующего поступательную пару со звеном 4, равна заданной угловой скорости звена 4, т. е. 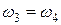 . Следовательно, для отыскания скоростей второго звена достаточно определить, кроме известной скорости точки В, скорость еще одной точки, а для третьего звена, кроме известной угловой скорости
. Следовательно, для отыскания скоростей второго звена достаточно определить, кроме известной скорости точки В, скорость еще одной точки, а для третьего звена, кроме известной угловой скорости 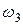 , также скорость какой-либо одной точки. Для решения этой задачи следует рассмотреть движение общей для этих двух звеньев точки С — центра средней вращательной пары.
, также скорость какой-либо одной точки. Для решения этой задачи следует рассмотреть движение общей для этих двух звеньев точки С — центра средней вращательной пары.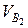 переносного (поступательного) движения звена со скоростью vB и скорости
переносного (поступательного) движения звена со скоростью vB и скорости 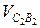 относительного (вращательного) движения звена 2 вокруг точки В:
относительного (вращательного) движения звена 2 вокруг точки В: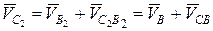 (2.6)
(2.6)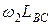 .
.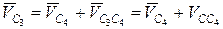 . (2.7)
. (2.7)


