
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоемкость газов. ЭнтропияСодержание книги
Поиск на нашем сайте
5.1. Основные определения Сообщение телу теплоты в каком-либо процессе вызывает изменение его состояния и в общем случае сопровождается изменением температуры. Отношение теплоты dq, полученное единицей количества вещества при бесконечно малом изменении его состояния, к изменению температуры dt называется удельной теплоемкостью тела в данном процессе:
Величина q в уравнении (5.1) зависит не только от интервала температур, но и от вида процесса подвода теплоты, характеризуемого некоторым постоянным параметром х, которым может быть объем тела υ, давление р и др. Общее количество теплоты, полученное в данном процессе, определяется выражением
Поскольку количество теплоты dq1-2,x зависит от характера процесса, то и теплоемкость системы сх зависит от условий протекания процесса. Массовая, объемная и мольная теплоемкости газов В термодинамике различают теплоемкости: массовую, объемную и мольную. Теплоемкость, отнесенную к 1 кг газа, называют массовой и обозначают сх. Измеряют эту теплоемкость в кДж/(кг • град). Теплоемкость, отнесенную к 1 м3 газа при нормальных физических условиях, т. е. при давлении 101325 Н/м2 и температуре 0° С, называют объемной и обозначают буквой с'х; измеряют ее в кДж/(м3 • град). Теплоемкость, отнесенную к 1 кмоль газа, называют мольной и обозначают μсх; измеряют ее в кДж/(кмоль·град). Между указанными теплоемкостями существует следующая связь:
где υ0 — удельный объем при нормальных термодинамических условиях; μ — молекулярная масса.
Аналитические выражения для теплоемкостей с υ и ср Как указывалось, теплоемкости зависят от характера процесса.
равная отношению количества теплоты dqv в процессе при постоянном объеме к изменению температуры dT тела, и теплоемкость при постоянном давлении
равная отношению количества теплоты dqp в процессе при постоянном давлении к изменению температуры dT тела. Из уравнения (5.4) следует, что в процессе при υ=const, в котором тело не совершает внешней работы, вся теплота, сообщаемая телу, идет на изменение его внутренней энергии:
или при cυ = const
Изменение внутренней энергии идеального газа равно произведению теплоемкости сv при постоянном объеме на разность температур тела в любом процессе. Дифференцируя уравнение I закона термодинамики по температуре при p=const и применяя уравнение Клайперона, получим для идеального газа:
Это уравнение носит название уравнения Майера. Оно может быть записано и для 1 кмоль:
Следовательно, для идеальных газов разность между μср и μсυ есть Для приближенных расчетов при не очень высоких температурах можно рекомендовать использование постоянных мольных теплоемкостей μСυ и μCр, полученных с некоторой корректировкой для трех- и многоатомных газов на основании молекулярно-кинетической теории теплоемкости. Эти данные приведены в табл. 5.1. Точные значения теплоемкостей идеальных газов в зависимости температуры приводятся в специальных таблицах. Таблица 5.1.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.105.119 (0.009 с.) |
|||||||||||||||||||||

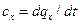 . (5.1)
. (5.1)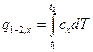 . (5.2)
. (5.2)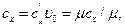 (5.3)
(5.3)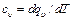 , (5.4)
, (5.4)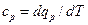 , (5.5)
, (5.5)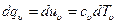 , (5.6)
, (5.6)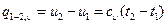 .
.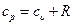 и
и 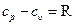 . (5.7)
. (5.7)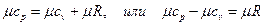 (5.8)
(5.8)


