
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическое выражение первого закона термодинамикиСодержание книги
Поиск на нашем сайте
Пусть 1 кг рабочего тела совершает некоторый процесс (рис. 4.2), на элементарном участке которого
С увеличением объема на Согласно закону сохранения энергии, можно написать для данного процесса следующее уравнение:
Полученное уравнение является математическим выражением первого закона термодинамики. Оно формулируется так: изменение внутренней энергии термодинамической системы равно алгебраической сумме полученной системой энергии в форме теплоты dl и совершенной ею внешней работой Все величины, входящие в уравнение (4.6), могут быть как положительными, так и отрицательными и в некоторых случаях могут принимать нулевые значения.
Энтальпия В позапрошлом столетии известный физик Томас Гиббс ввел в практику тепловых расчетов новую функцию, которую назвал энтальпией. Удельная энтальпия, т. е. энтальпия, отнесенная к 1 кг, обозначается буквой
Поскольку входящие в энтальпию величины Энтальпия идеального газа так же, как и внутренняя энергия, является функцией только температуры и не зависит от других параметров. Если в качестве независимых параметров выбрать давление
Отсюда
или
Интеграл При
Дифференциал энтальпии
т.е энтальпия – “теплосодержание”.
Рис. 4.3
Физический смысл энтальпии будет понятен из рассмотрения следующего примера. На перемещающийся поршень в цилиндре с 1 кг газа помещена гиря массой
Произведение
Произведение давления на объем есть работа, которую надо затратить, чтобы ввести газ объемом Если рассматривать газ, находящийся в цилиндре, и поршень с грузом как одну систему, которую будем называть расширенной системой, то полная энергия
Отсюда видно, что энтальпия Значения энтальпии для паров, газов, газовых смесей приводятся в технической и справочной литературе.
При t0=0 °C величину энтальпии i0 принимают равной нулю. Энтальпия имеет большое значение и применение при расчётах тепловых машин, холодильных и калориферных установок и позволяет значительно упростить тепловые расчёты. Она позволяет применять графические методы при исследовании различных термодинамических поцессов и циклов (например is – и id – диаграммы для водяного пара и влажного воздуха).
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 93; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.188.174 (0.009 с.) |

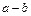 подводится бесконечно малое количество энергии в форме теплоты
подводится бесконечно малое количество энергии в форме теплоты 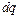 ; при этом температура и объем тела увеличиваются соответственно на бесконечно малые величины
; при этом температура и объем тела увеличиваются соответственно на бесконечно малые величины 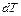 и
и 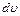 .
.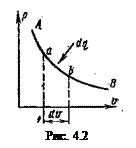 С повышением температуры тела на
С повышением температуры тела на 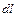 .
.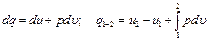 . (4.6)
. (4.6) и измеряется в килоджоулях на килограмм (кДж/кг); она представляет собой, по определению, сложную функцию вида
и измеряется в килоджоулях на килограмм (кДж/кг); она представляет собой, по определению, сложную функцию вида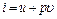 . (4.7)
. (4.7)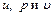 являются параметрами (функциями) состояния, следовательно, и сама энтальпия будет также параметром (функцией) состояния.
являются параметрами (функциями) состояния, следовательно, и сама энтальпия будет также параметром (функцией) состояния.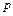 и температуру
и температуру 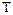 , то можно получить другой вид аналитического выражения первого закона термодинамики:
, то можно получить другой вид аналитического выражения первого закона термодинамики: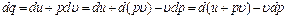 .
.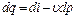 , (4.8)
, (4.8)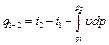 . (4.9)
. (4.9)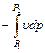 представляет собой чисто математическую величину и приобретает конкретное физическое содержание лишь при рассмотрении процессов истечения рабочего тела (см. разд. 10).
представляет собой чисто математическую величину и приобретает конкретное физическое содержание лишь при рассмотрении процессов истечения рабочего тела (см. разд. 10).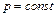 уравнение (4.8) превращается в
уравнение (4.8) превращается в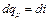 . (4.10)
. (4.10)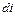 есть элементарное количество теплоты, участвующее в процессе при постоянном давлении. Вся теплота в процессе при постоянном давлении расходуется на изменение энтальпии:
есть элементарное количество теплоты, участвующее в процессе при постоянном давлении. Вся теплота в процессе при постоянном давлении расходуется на изменение энтальпии: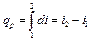 , (4.11)
, (4.11)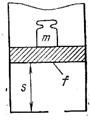
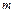 кг (рис. 4.3). Площадь поршня
кг (рис. 4.3). Площадь поршня 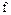 , внутренняя энергия рабочего тела
, внутренняя энергия рабочего тела 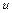 . Потенциальная энергия гири равна произведению массы гири
. Потенциальная энергия гири равна произведению массы гири 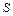 . Так как давление газа
. Так как давление газа 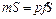 .
.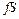 есть удельный объем газа. Отсюда
есть удельный объем газа. Отсюда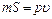 .
.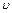 во внешнюю среду с давлением
во внешнюю среду с давлением 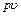 есть потенциальная энергия газа, зависящая от сил, действующих на поршень. Чем больше эти внешние силы, тем больше давление
есть потенциальная энергия газа, зависящая от сил, действующих на поршень. Чем больше эти внешние силы, тем больше давление 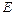 этой системы складывается из внутренней энергии газа u и потенциальной энергии поршня с грузом, равной
этой системы складывается из внутренней энергии газа u и потенциальной энергии поршня с грузом, равной 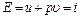 . (4.12)
. (4.12)


