
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Й способ. С помощью 2-й производной.Содержание книги Поиск на нашем сайте
Выясним знак 2-й производной в этих точках.
Ответ.
Задача 249. Найти экстремумы функции Решение. Производная: Чтобы определить, где максимум, а где минимум, выясним знак 2-й производной в этих же точках.
Ответ.
Задача 250. Найти экстремумы для Решение. Точки, в которых производная обращается в 0, это 0,1 и 2. Вычислим знак 2-й производной в каждой из этих точек.
Ответ.
Задача 251. Найти экстремумы функции Решение. Первая производная: Она обращается в 0 при Рассмотрим знак производной на интервалах. Множитель
Ответ. Единственный экстремум Задача 252. Найти интервалы монотонности и экстремумы функции Решение.
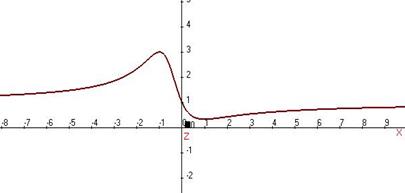
От знаменателя знак не зависит, знаменатель тут всегда строго больше 0. Поэтому всё зависит только от знака числителя. Выделим множитель, который может менять свой знак: На интервалах На интервале В точке В точке Кстати, в этом примере с помощью интервалов узнать экстремумы проще, чем с помощью 2-й производной, ведь пришлось бы считать поизводную от дроби Для построения графика можем найти высоту в точках максимума и минимума: Вот как выглядит график:
Ответ.
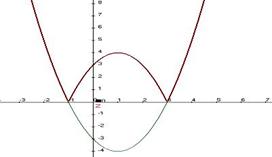
Задача 253. Найти интервалы монотонности и экстремумы функции Решение. Сначала найдём корни выражения под знаком модуля, чтобы понять, какая часть параболы отражается вверх.
Тогда знак меняется на интервале График:
Производная: Производная разрывна при Выбирая целочисленную точку на каждом интервале, найдём знак производной на этом интервале. Таким образом, Ответ.
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.58.90 (0.008 с.) |

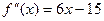 .
. 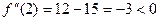
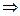
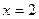 максимум.
максимум.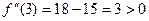
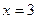 минимум.
минимум.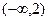 возрастание,
возрастание,  убывание,
убывание, 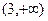 возрастание.
возрастание.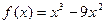 и разность между ординатами максимума и минимума.
и разность между ординатами максимума и минимума.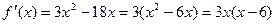 . Стационарные точки (где производная = 0)
. Стационарные точки (где производная = 0) 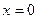 и
и 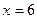 .
.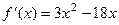
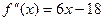 .
.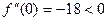 , точка
, точка 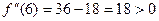 точка
точка 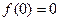 ,
, 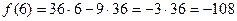 .
.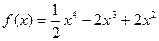 .
.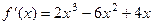 =
= 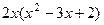 =
= 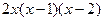 .
.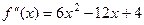 .
.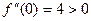
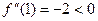

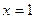 максимум.
максимум.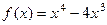 .
.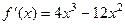 =
= 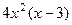 .
.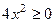 , знак может менять только
, знак может менять только 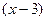 . Достаточно рассмотреть знак производной при каком-либо целом значении на каждом из интервалов
. Достаточно рассмотреть знак производной при каком-либо целом значении на каждом из интервалов 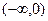 ,
, 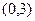 и
и 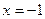 и
и 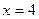 положительна. Итак, экстремум всего 1, это точка
положительна. Итак, экстремум всего 1, это точка 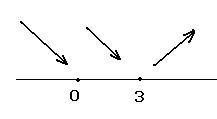
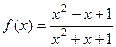 .
. 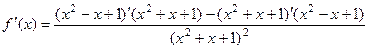 =
=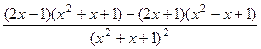 =
=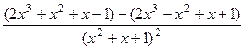 =
= 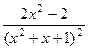 .
.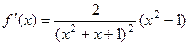 . Корни
. Корни 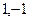 .
.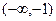 и
и 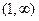 :
: 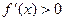 , рост.
, рост.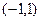 :
: 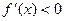 убывание.
убывание.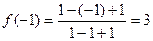 ,
, 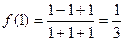 .
.
 .
. ,
, 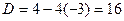 ,
, 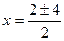 , корни
, корни 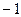 и 3.
и 3.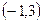 , то есть функцию можно записать в виде:
, то есть функцию можно записать в виде: 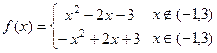 .
. 
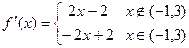 .
. 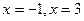 и обращается в 0 при
и обращается в 0 при 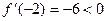 убывание на
убывание на 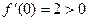 рост на
рост на 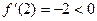 убывание на
убывание на  .
.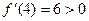 рост на
рост на 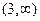 .
.


