
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи со следствиями из 1 и 2 зам. Пределов.Содержание книги Поиск на нашем сайте
Приходовский М.А. Математика Курс практических занятий Семестр 1 Группы 520, 530 Томск ТУСУР 2020
В связи с переполнением файла и невозможностью обработки больших файлов редактором Word, материалы практики после № 18 идут отдельным файлом. Таблица соответствия недель, задач и номеров практик.
Практика 19. Предел функции. Сначала рассмотрим примеры, где Задача 181. Найти предел Решение. Так как переменная неограниченно возрастает, то тоже влияют её старшие степени и коэффициенты перед ними. Сократим дробь: Ответ. Задача 182. Найти предел Решение. Аналогично тому, как в прошлом примере, сократим на старшую степень, здесь это
Ответ. Задача 183. Найти предел Решение. В этом примере надо домножить и поделить на «сопряжённое» то есть на сумму, чтобы использовать формулу
В знаменателе можно представить
Задача 184. Найти предел Решение. Заметим, что
Ответ. 0.
Задача 185(А,Б). Найти пределы Решение. Сейчас на этом примере мы увидим, как может отличаться ответ в зависимости от Если
А вот если
Ответы. 4 и
Примеры, в которых Задача 186. Найти предел Решение. В этом случае
Когда сократили, тогда уже можно просто подставить Ответ. 2. Задача 187. Найти предел Решение. Найдём корни многочленов в числителе и знаменателе, и разложим на множители. = Ответ. Задача 188. Найти предел Решение. Разложим на множители, как и в прошлой задаче.
Нашли корни числителя и знаменателя, разложили на множители. Сократили тот множитель, который отвечает за стремление к нулю, в числителе и знаменателе. Ответ.
Задача 189. Найти предел Решение. Во-первых, если просто подставить
Ответ. Задача 190. Найти предел Решение. Способ 1. Тот факт, что при подстановке
Способ 2. (Лопиталя).
Ответ. Задача 191. Найти предел Решение. Способ 1.
Способ 2.
Задача 192. Найти предел Решение. Воспользуемся формулой разности кубов:
Впрочем, можно сделать и методом Лопиталя:
Ответ. 27.
Задача 193. Найти предел Решение. Ответ. 2.
Задача 194 (А,Б). Найти Решение. Сразу вынесем за скобку общий множитель и в числителе, и в знаменателе, там все остальные коэффициенты ему кратны. Затем разложим на множители.
А при
Ответы. Замечание. Оба этих предела можно было найти по правилу Лопиталя.
Задача 195. Найти предел Решение. Домножим и разделим на сопряжённое к каждой разности.
При этом соединим дугой те, которые в итоге сворачиваются в разность квадратов. Прочие множители, которые ни с чем не объединяются, вынесем в отдельную дробь, и даже в отдельный предел. Получается произведение пределов:
В одном из них нет неопределённости, а во втором преобразуем так, чтобы сократить скобку
Ответ. Задача 196. Найти предел Решение. В этом случае можно с помощью замены преобразовать так, что будут только целые степени, а для получившихся многочленов уже можно искать корни и проводить разложение на множители. НОК(2,3) = 6. Если обозначим
При этом, если * Такое совпадение при замене переменной бывает далеко не всегда, а лишь в частных случаях, а обычно надо пересчитать, возможно новая переменная стремится к другому числу. Например, если Итак,
При этом даже нет необходимости делать обратную замену и возвращаться к старой переменной. Ответ.
Практика 20. 1-й, 2-й замеч. пределы и их следствия. «1-й замечательный предел». Вспомнить теорию:
Следствия из 1-го замечательного предела:
Задача 197. Найти предел Решение. С помощью преобразований получим в знаменателе такое же выражение, как под знаком синуса в числителе.
Второй предел вообще не содержит неопределённости, а первый это в точности Ответ. Задача 198. Найти предел Решение. Ответ. 5.
Задача 199. Найти предел Решение.
Сначала домножили на сопряжённое выражение, потом вынесли в отдельный множитель ту часть, где нет неопределённости. В конце домножили на 6 в знаменателе и числителе, чтобы в знаменателе образовалось ровно такое же выражение, как под знаком синуса, то есть Ответ. 24. Задача 200. Найти предел Решение. Эту задачу можно решить с применением тригонометрических формул. Способ 1. По формуле
Способ 2. Ответ. 2.
Задача 201. Найти предел Решение.
Ответ. 3.
«2-й замечательный предел». Вспомнить формулы:
Следствия из 2-го замечательного предела. Эквивалентности бесконечно малых, следующие из 2 зам. lim
Задача 202. Найти предел Решение. Здесь целая часть 1 выделена в явном виде. Остаётся только домножить и найти предел в степени.
Ответ. Задача 203. Найти предел Решение.
Ответ. Задача 204. Найти предел Решение. Здесь неопределённость
Слагаемое, которое следует после 1, стремится к 0, что и должно быть для 2 замечательного предела. Далее,
Задача 205. Найти предел Решение. Здесь сначала заметим, что основание стремится к 7/7 = 1. А степень к бесконечности. То есть, неопределённость типа
использовали тот факт, что Далее, получаем
Ответ. Задача 206. Найти предел Решение. Заметим, что основание стремится к 1, неопределённость типа
Ответ.
Задача 207. Найти предел Решение.
Ответ.
Замечание. Некоторые особенности вычислений, в которых не требуется второй замечательный предел. Если основание стремится не к 1, а к числу a<1 а степень к бесконечности, то можно сразу сделать вывод, что предел 0. Если a>1 то наоборот,
Если основание и показатель стремятся к
Практика 21. Асимптоты. Если Горизонтальные: Если
Пример.
Вертикальные: Если
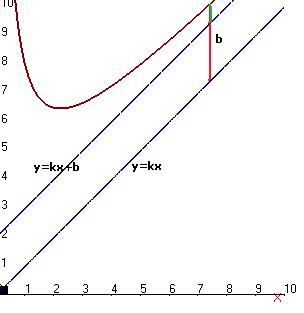
Наклонные асимптоты. Задача 219. Вывод формул Так как точка на графике и на асимптоте сближаются то:
Отсюда следует, что
Рассмотрим прямую Если разность ординат для точки на графике и соответствующей точки на прямой Если две величины, Тогда рассмотрим
Итак, мы получили формулы для нахождения Пример 220. Найти асимптоты графика функции Решение. Во-первых, сразу видно точку разрыва 2-го рода Найдём наклонную асимптоту.
Обратите внимание: здесь предел одинаково вычисляется при Найдём Ответ. Вертикальная x = 2, наклонная y = x + 2. График выглядит так:
Задача 221. Найти асимптоты графика функции Решение. Во-первых, знаменатель не обращается в 0, поэтому точек разрыва 2-го рода нет, и нет вертикальных асимптот. Горизонтальных асимптот также нет, т.к. Ищем наклонные асимптоты.
Ответ. Асимптота
Задача 222. Найти асимптоты графика функции Решение. Во-первых, при
Ответ. Вертикальная
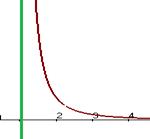
Задача 223. Найти асимптоты графика функции Решение. Область определения:
здесь умножили на сопряжённое, как в таких пределах делали раньше.
Итак, Ответ. Две односторонние асимптоты График (асимптоты показаны зелёным цветом).
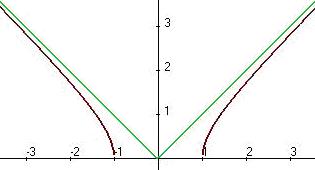
Задача 224. Найти асимптоты графика функции Решение. Функция не является чётной, поэтому здесь придётся при
Итак, На левой полуплоскости:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

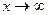 . Методы решения для последовательности (
. Методы решения для последовательности (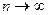 ) и для функции при
) и для функции при 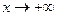 во многом очень похожи: для последовательности величина дискретно увеличивается, для функции - непрерывно, но всё равно и там, и здесь неограниченное возрастание.
во многом очень похожи: для последовательности величина дискретно увеличивается, для функции - непрерывно, но всё равно и там, и здесь неограниченное возрастание.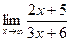 .
. 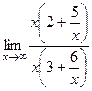 =
= 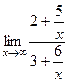 =
= 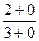 =
= 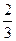 .
.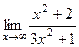 .
. 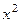 .
.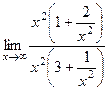 =
= 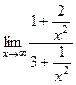 =
= 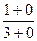 =
= 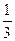 .
. 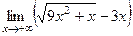 .
. 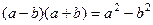 .
.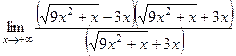 =
= 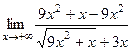 =
= 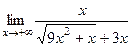 теперь сократим на
теперь сократим на 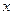 :
: 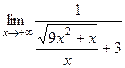
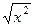 , чтобы упростить выражение в знаменателе:
, чтобы упростить выражение в знаменателе: 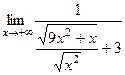 =
= 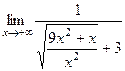 =
= 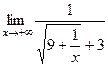 =
= 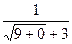 =
= 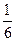 . Ответ.
. Ответ. 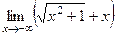 .
. , то есть указанная сумма, фактически, есть разность. Домножаем на сопряжённое выражение, которое формально будет разностью, а на самом деле - суммой:
, то есть указанная сумма, фактически, есть разность. Домножаем на сопряжённое выражение, которое формально будет разностью, а на самом деле - суммой: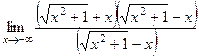 =
=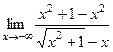 =
= 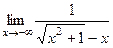 . Здесь в знаменателе разность, но 2-я величина отрицательна, то есть фактически - сумма бесконечно-больших. Тогда получается, что дробь - величина, обратная к бесконечно-большой, т.е. бесконечно-малая.
. Здесь в знаменателе разность, но 2-я величина отрицательна, то есть фактически - сумма бесконечно-больших. Тогда получается, что дробь - величина, обратная к бесконечно-большой, т.е. бесконечно-малая. 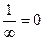 .
.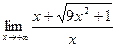 ,
, 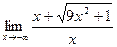 .
. или
или  . И в том, и в другом случае мы стараемся сократить дробь на множитель
. И в том, и в другом случае мы стараемся сократить дробь на множитель 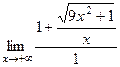 =
= 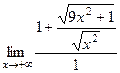 =
= 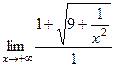 =
= 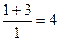 .
.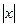 , оно положительно, то есть при
, оно положительно, то есть при 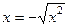 . Поэтому
. Поэтому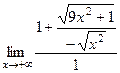 =
= 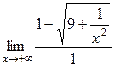 =
= 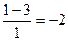 .
.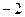 .
. 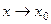 .
.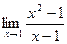 .
. 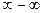 или
или 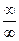 , то здесь
, то здесь 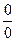 . Если просто подставить 1 в это выражение, получилось бы
. Если просто подставить 1 в это выражение, получилось бы 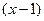 и в числителе, и в знаменателе, чтобы его сократить.
и в числителе, и в знаменателе, чтобы его сократить.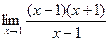 =
= 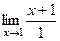 = 2.
= 2.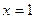 .
.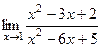 .
.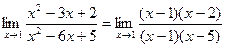 =
=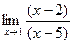 =
= 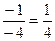 . Сократили тот множитель, который отвечает за стремление к нулю, в числителе и знаменателе.
. Сократили тот множитель, который отвечает за стремление к нулю, в числителе и знаменателе.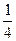 .
.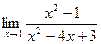 .
.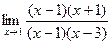 =
= 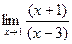 =
= 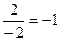 .
.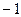 .
.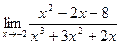 .
.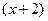 и в числителе, и в знаменателе найдётся. Это облегчает поиск корней, можно обойтись даже без дискриминанта, а просто найти второй дополняющий. Когда мы сократим все
и в числителе, и в знаменателе найдётся. Это облегчает поиск корней, можно обойтись даже без дискриминанта, а просто найти второй дополняющий. Когда мы сократим все 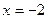 в оставшееся выражение.
в оставшееся выражение.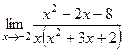 =
= 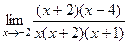 =
= 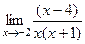 =
= 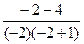 =
= 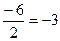 .
.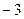 .
.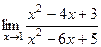 .
.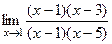 =
= 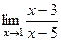 =
= 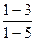 =
= 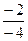 =
= 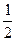 .
.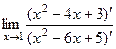 =
= 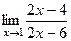 =
= 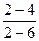 =
= 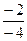 =
= 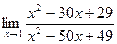 .
. 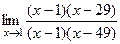 =
= 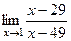 =
= 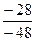 =
= 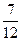 .
.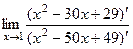 =
= 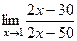 =
= 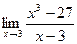 .
.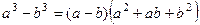 .
.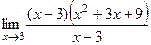 =
= 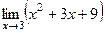 = 27.
= 27.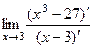 =
= 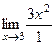 = 27.
= 27.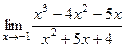 .
. 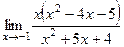 =
= 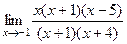 =
= 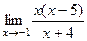 =
= 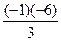 = 2.
= 2.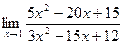 и
и 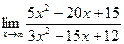 .
.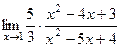 =
= 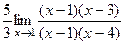 =
=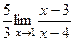 =
= 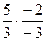 =
= 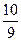 .
. 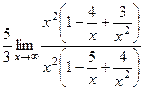 =
= 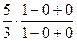 =
= 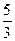 .
.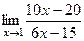 =
= 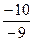 =
= 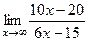 =
= 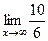 =
= 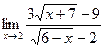 .
.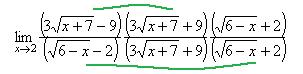
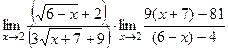
 .
.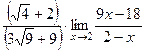 =
= 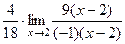 =
=  =
= 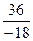 =
= 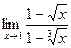 .
. 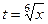 , то:
, то: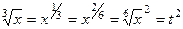 ,
, 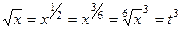 .
.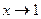 , то и
, то и 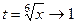 тоже стремится к 1.
тоже стремится к 1.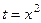 и
и 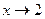 , то
, то 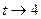 .
.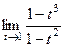 =
= 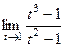 (для удобства сделали, чтобы многочлены начинались со старшей степени). Далее,
(для удобства сделали, чтобы многочлены начинались со старшей степени). Далее, 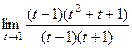 =
= 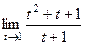 =
= 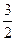 .
. 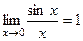 .
.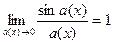 ,
, 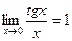
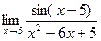 .
. 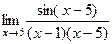 =
= 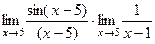 =
= 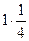 =
= 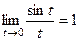 если переобозначить
если переобозначить 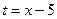 .
.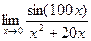 .
.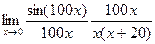 =
= 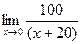 = 5.
= 5.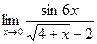 .
.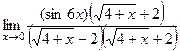 =
=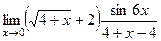 =
= 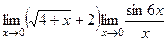 =
=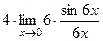 = 24.
= 24.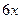 .
. 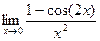 .
.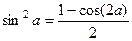 . Получается
. Получается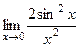 =
= 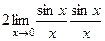 = 2.
= 2.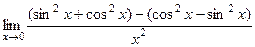 =
= 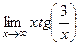 .
.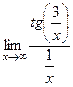 =
= 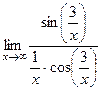 =
=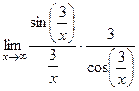 = (замена
= (замена 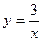 )
) 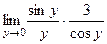 =
=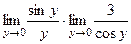 =
=  .
. 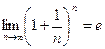
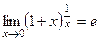
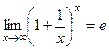
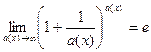 ,
, 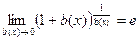 .
.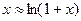
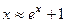
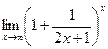 .
.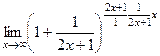 =
= 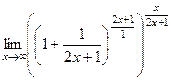 =
=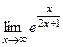 =
= 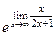 =
= 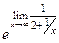 =
= 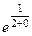 =
= 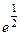 =
= 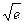 .
. 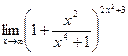 .
.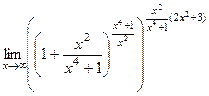 =
= 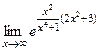 =
=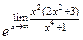 =
= 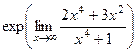 =
= 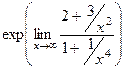 =
= 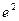 .
.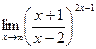 .
.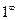 . Основание стремится к 1, так как здесь одинаковые старшие степени многочленов в числителе и знаменателе, и одинаковые коэффициенты при них. Отделим от дроби её целую часть, то есть 1.
. Основание стремится к 1, так как здесь одинаковые старшие степени многочленов в числителе и знаменателе, и одинаковые коэффициенты при них. Отделим от дроби её целую часть, то есть 1. 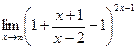 =
= 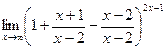 =
= 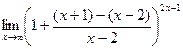 =
= 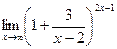 .
.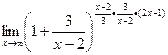 =
= 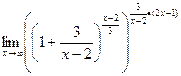 =
= 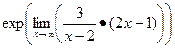 =
= 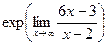 =
= 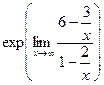 =
=  . Ответ.
. Ответ.  .
.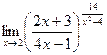 .
.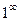 и можно использовать 2-й замечательный предел. Сначала выделяем целую часть дроби, то есть 1. Прибавим и отнимем 1, но ту, которую отняли, представим в таком виде, чтобы она объединилась с дробью.
и можно использовать 2-й замечательный предел. Сначала выделяем целую часть дроби, то есть 1. Прибавим и отнимем 1, но ту, которую отняли, представим в таком виде, чтобы она объединилась с дробью. 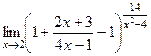 =
= 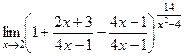 =
=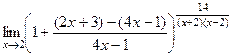 =
= 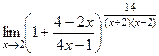 теперь после 1 следует бесокнечно-малая, которая обращается в 0 при
теперь после 1 следует бесокнечно-малая, которая обращается в 0 при 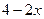 . Далее, в степени домножаем обратную к этой дроби, но при этом и её саму тоже, чтобы ничего не изменилось.
. Далее, в степени домножаем обратную к этой дроби, но при этом и её саму тоже, чтобы ничего не изменилось.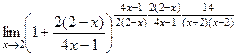 =
= 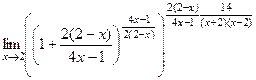 =
= 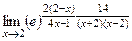
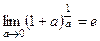 .
.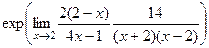 =
=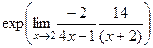 =
= 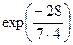 =
= 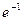 .
. 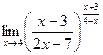 .
.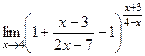 =
= 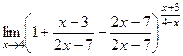 =
=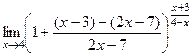 =
= 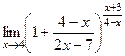 =
= 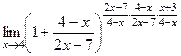 =
= 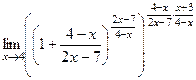 =
=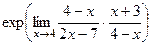 =
= 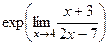 =
= 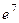 .
. 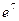 .
.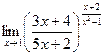 .
. 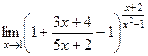 =
= 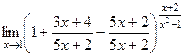 =
= 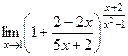 =
=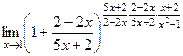 =
= 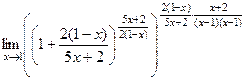 =
=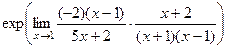 =
= 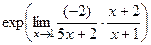 =
= 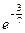 .
.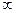 .
.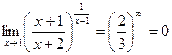 ,
, 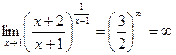 .
.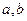 соответственно, то 2-й зам. предел не требуется, а ответ
соответственно, то 2-й зам. предел не требуется, а ответ 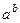 .
.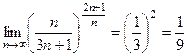 .
. 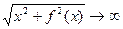 то
то 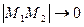 .
.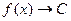 ,
, 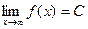 .
.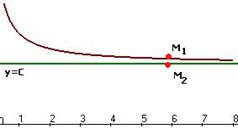
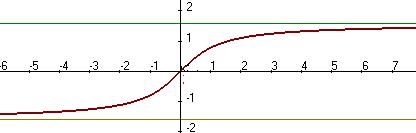
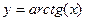 две односторонние горизонтальные асимптоты:
две односторонние горизонтальные асимптоты: 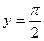 и
и 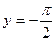 .
.
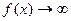 ,
, 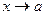 , то асимптота вертикальная (это соответствует разрыву 2 рода,
, то асимптота вертикальная (это соответствует разрыву 2 рода, 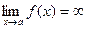 ).
).
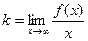 и
и 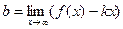 .
.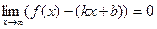 .
.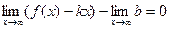 , то есть
, то есть 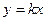 , параллельную асимптоте
, параллельную асимптоте 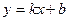 .
.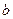 . Отрезок, соответствующий этому расстоянию, отмечен красным на чертеже.
. Отрезок, соответствующий этому расстоянию, отмечен красным на чертеже.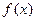 и
и 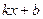 , неограниченно возрастают, и при этом разность между ними стремится к 0, то их отношение стремится к 1, то есть
, неограниченно возрастают, и при этом разность между ними стремится к 0, то их отношение стремится к 1, то есть 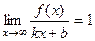 . Но ведь также очевидно, что
. Но ведь также очевидно, что 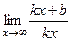 =
= 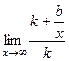 = 1.
= 1.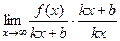 , этот предел равен 1. Однако если сократить в нём
, этот предел равен 1. Однако если сократить в нём 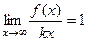 , а тогда
, а тогда 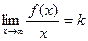 .
.
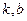 . На практике сначала надо найти
. На практике сначала надо найти 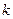 , а уже затем
, а уже затем 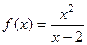 .
.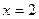 . Есть вертикальная асимптота
. Есть вертикальная асимптота 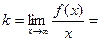
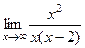 (мы просто добавили лишний
(мы просто добавили лишний 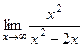 =
= 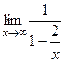 = 1. Итак,
= 1. Итак, 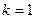 .
.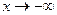 , но бывают примеры, в которых по-разному, то есть на правой и левой полуплоскости могут быть разные асимптоты.
, но бывают примеры, в которых по-разному, то есть на правой и левой полуплоскости могут быть разные асимптоты.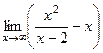 =
= 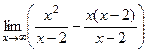 =
= 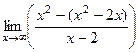 =
= 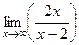 =
= 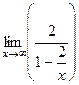 = 2.
= 2.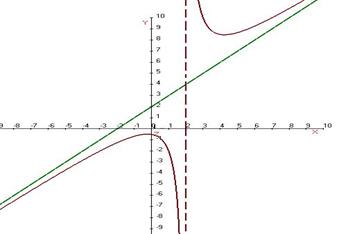
 .
.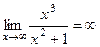 , предел не константа С.
, предел не константа С.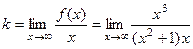 =
= 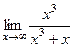 = 1.
= 1.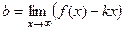 =
= 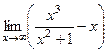 =
= 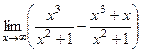 =
=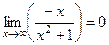 . Асимптота
. Асимптота 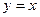 . Чертёж:
. Чертёж: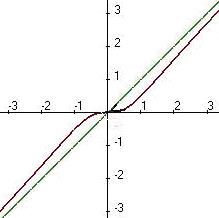
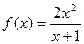 .
.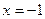 знаменталь обращается в 0, здесь разрыв 2 рода. То есть, вертикальная прямая
знаменталь обращается в 0, здесь разрыв 2 рода. То есть, вертикальная прямая 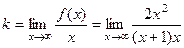 =
= 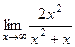 = 2. Причём этот результат не зависит от того, предел при
= 2. Причём этот результат не зависит от того, предел при 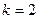 , т.е. есть наклонная асимптота типа
, т.е. есть наклонная асимптота типа 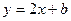 . теперь найдём
. теперь найдём 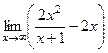 =
= 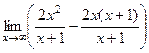 =
=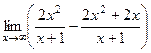 =
= 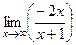 =
= 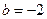 и опять же, это независимо от
и опять же, это независимо от 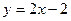 это двусторонняя асимптота.
это двусторонняя асимптота.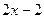 . График:
. График: 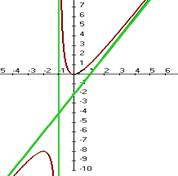
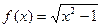 .
.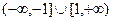 . Здесь нет знаменателя, который мог бы обращаться в 0, поэтому вертикальных асимптот нет. Функция не ограниченная при
. Здесь нет знаменателя, который мог бы обращаться в 0, поэтому вертикальных асимптот нет. Функция не ограниченная при 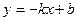 на левой. А вот двусторонняя асимптота здесь никак не могла бы быть, ведь график симметричен относительно вертикальной оси, т.к. функция чётная.
на левой. А вот двусторонняя асимптота здесь никак не могла бы быть, ведь график симметричен относительно вертикальной оси, т.к. функция чётная.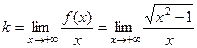 =
= 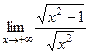 =
= 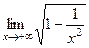 = 1.
= 1.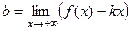 =
= 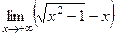 =
= 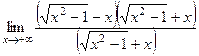
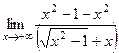 =
= 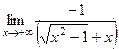 =
= 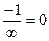 .
.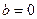 , на правой полуплоскости асимптота
, на правой полуплоскости асимптота 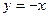 .
.
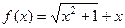 .
.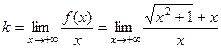 =
= 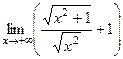 =
= 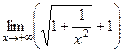 =
= 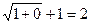 .
.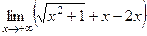 =
= 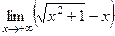 =
=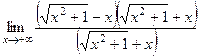 =
= 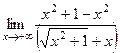 =
= 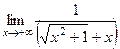 = 0.
= 0. .
.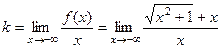 =
= 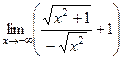 =
=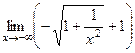 =
= 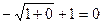 .
.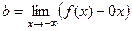 =
= 


