
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность и точки разрыва.
Определение. Обозначается Аналогично, Обозначается Определение. Функция называется непрерывной в точке
Если это не выполняется, точка называется точкой разрыва.
Типы точек разрыва.
Примеры
Задача 212. Найти точку разрыва и охарактеризовать её тип: Решение. Здесь при любом
Ответ. Разрыв 1 рода Задача 213. Охарактеризовать тип точки Решение. Односторонние пределы для этой функции таковы:
Ответ. Разрыв 1 рода.
Задача 214. Исследовать тип разрыва Решение. И при К тому же функция чётная, и так ясно, что с двух сторон симметричные ветви графика. Так что достаточно было вычислить только с одной стороны. Ответ. Примечание. График этой функции:
Задача 215. Найти точки разрыва и определить их тип Решение. Вычислить значение функции обычным путём здесь нельзя лишь в точках Во-первых, можно представить так: Надо найти оба односторонних предела в каждой из точек. Рассмотрим Для предела справа,
Для предела слева,
Получились разные константы. Значит, разрыв 1-го рода.
Рассмотрим Здесь
Хотя бы с одной стороны предел Ответ.
Чертёж к этой задаче. Синим цветом показан график этой функции, жёлтым - вертикальная асимптота, где разрыв 2-го рода.
Задача 216. Исследовать тип точки разрыва Решение. Ищем односторонние пределы вокруг 0, но при этом каждый раз домножаем и делим на
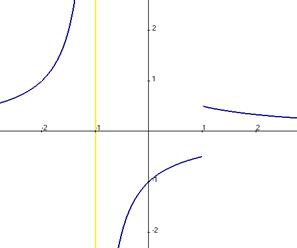
Здесь знак модуля раскрывается по-разному в зависимости от того, справа или слева от 0 мы находимся. Это либо Ответ. Примечание. Вот график этой функции:
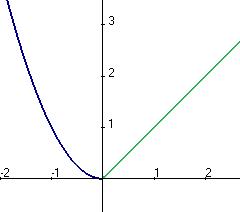
Задача 217. Выяснить тип точки Решение. Левосторонний предел здесь должен вычисляться с помощью первой ветви функции, а правосторонний с помощью второй. Значение функции существует и равно как левостороннему пределу, так и правостороннему. 0 это точка непрерывности. Ответ. График этой функции:
Задача 218. Найти точки разрыва и определить их тип для функции: Решение. Сначала ищем точки, подозрительные на разрыв, то есть где возможен разрыв. Во-первых, это точка стыковки двух ветвей графика, то есть Рассмотрим
Тогда Рассмотрим
Рассмотрим
Ответ.
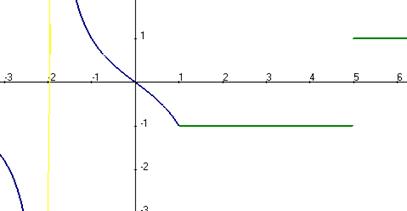
На графике синим цветом показана левая ветвь функции, зелёным - правая, жёлтым - асимптота (она там, где разрыв 2 рода). График этой функции:
Асимптоты. Если Горизонтальные: Если
Пример.
Вертикальные: Если
Наклонные асимптоты. Задача 219. Вывод формул Так как точка на графике и на асимптоте сближаются то:
Отсюда следует, что
Рассмотрим прямую Если разность ординат для точки на графике и соответствующей точки на прямой Если две величины, Тогда рассмотрим
Итак, мы получили формулы для нахождения Пример 220. Найти асимптоты графика функции Решение. Во-первых, сразу видно точку разрыва 2-го рода Найдём наклонную асимптоту.
Обратите внимание: здесь предел одинаково вычисляется при Найдём Ответ. Вертикальная x = 2, наклонная y = x + 2. График выглядит так:
Задача 221. Найти асимптоты графика функции Решение. Во-первых, знаменатель не обращается в 0, поэтому точек разрыва 2-го рода нет, и нет вертикальных асимптот. Горизонтальных асимптот также нет, т.к. Ищем наклонные асимптоты.
Ответ. Асимптота
Задача 222. Найти асимптоты графика функции Решение. Во-первых, при
Ответ. Вертикальная
Задача 223. Найти асимптоты графика функции Решение. Область определения:
здесь умножили на сопряжённое, как в таких пределах делали раньше.
Итак, Ответ. Две односторонние асимптоты График (асимптоты показаны зелёным цветом).
Задача 224. Найти асимптоты графика функции Решение. Функция не является чётной, поэтому здесь придётся при
Итак, На левой полуплоскости:
=
Ответ. На правой полуплоскости наклонная асимптота на левой горизонтальная асимптота
Задача дом-1. Найти асимптоты графика функции Ответ. Вертикальные асимптоты Задача дом-2. Найти асимптоты графика функции Ответ. Вертикальная: Практика 22. Дифференциальное исчисление функции одной переменной. Дифференциал, уравнение касательной. Метод Лопиталя.
Законы дифф. суммы и разности, произведения, частного.
Закон дифференцирования композиции, обратной функции.
Задача 225. Вывести формулу Решение. По определению, преобразуем:
Задача 226. Доказать, что Задача 227. Доказать, что Запишем производную по определению.
Но тут есть сдвиг на
Теперь можно вынести тот множитель, который одинаков в каждой разности:
Видно, то, что осталось в дробях, это и есть производные для u или v соответственно, т.е. в итоге:
Задача 227-Б. Вывести формулу Решение. Объединим первые 2 слагаемых в один условный множитель, а третье пусть будет вторым множителем. После этого применим известную формулу, доказанную для 2 множителей.
выражению
Задача 228. С помощью определения доказать, что Решение.
воспользуемся тригонометрической формулой понижения степени
= = Ответ. Задача 229. Вычислить производную от композиций: А) Решение. А) Б) Ответы.
Задача 230. Найти производную от Решение. Здесь композиция трёх функций. Сначала действует степенная и переводит Ответ.
Задача 231. Найти производную функции Решение. Способ 1. Можно рассматривать как композицию, тогда:
Способ 2. Можно рассматривать сразу как степенную функцию с дробной степенью, тогда решение такое: Как мы видим, двумя способами получаем одно и то же. Ответ. Задача 232. Найти 1 и 2 производную от Решение.
Вторая производная: Ответ.
Задача 233. Найти производную от Решение. Здесь нельзя применять формулу степенной функции, ведь в показателе тоже есть переменная. Но нельзя и формулу показательной функции, т.к. в основании тоже есть переменная. Единственным выходом здесь является логарифмирование, чтобы
После приведения подобных, получим Ответ.
Задача 234. Найти 1-ю и 2-ю производную для Решение. = = =
Следующая, 2-я производная:
Вычислим «тестовое» значение при конкретном
Ответ. Задача домашняя. Найти 1-ю и 2-ю производную для Ответ. - - - Перерыв - - -
Задача 235. Найти 1-ю и 2-ю производную Решение.
Ответ. Задача 236. Дана функция Найти Решение.
= Максимально возможно привели подобные, чтобы затем было легче считать 2-ю производную.
= Вычислим Ответ.
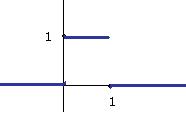
Задача 237. Нарисовать график
Решение. Здесь мы можем рассуждать следующим образом. Запишем функцию на каждом из участков:
Тогда можно найти производную на каждом участке отдельно:
Тогда график производной выглядит так:
Функция называется дифференцируемой в точке
где Главная линейная часть приращения функции, а именно Обозначается также через (Вспомнить: главная часть бесконечно-малой). Примечание. Бывают не дифференцируемые функции, например Уравнение касательной. В этом уравнении,
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 152; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.182.45 (0.223 с.) |
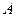 называется правосторонним пределом функции
называется правосторонним пределом функции 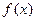 в точке
в точке 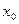 , если:
, если: 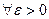
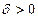 , так, что при
, так, что при 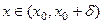 выполняется:
выполняется: 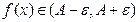 .
.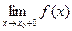 .
.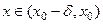 выполняется:
выполняется: 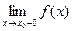 .
.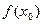 , и оно совпадает как с правосторонним так и с левосторонним пределами:
, и оно совпадает как с правосторонним так и с левосторонним пределами: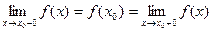 .
.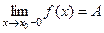
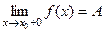
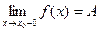
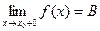 ,
, 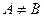 .
.
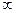 или не сущ.
или не сущ.
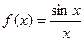
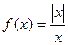
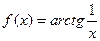
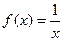
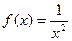
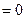
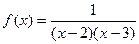 точки разрыва 2 и 3.
точки разрыва 2 и 3.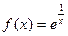 . Предел слева равен 0, справа
. Предел слева равен 0, справа 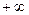 . График:
. График: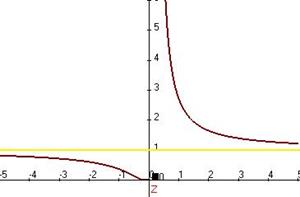
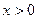 верно
верно 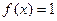 , а при любом
, а при любом  верно
верно 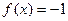 . В точке 0 односторонние пределы различны.
. В точке 0 односторонние пределы различны.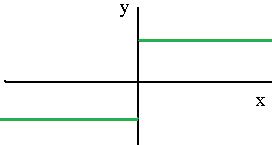
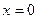 , если
, если 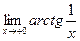 =
= 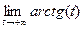 =
= 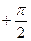 , т.к. если
, т.к. если 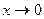 и при этом
и при этом 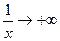 .
.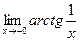 =
= 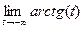 =
= 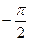 , т.к. если
, т.к. если 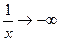 .
.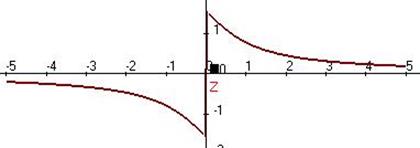
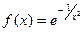 .
.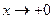 , и при
, и при 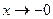 здесь
здесь 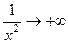 , а тогда
, а тогда 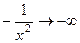 . Тогда для обоих односторонних пределов получается одинаково:
. Тогда для обоих односторонних пределов получается одинаково: 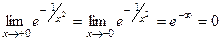 . Тогда разрыв устранимый.
. Тогда разрыв устранимый.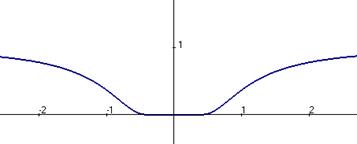
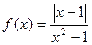 .
.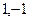 где знаменатель обращается в 0. Эти две точки подозрительные на существование разрыва, мы и будем исследовать.
где знаменатель обращается в 0. Эти две точки подозрительные на существование разрыва, мы и будем исследовать.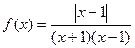 .
.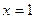 .
.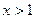 и модуль раскрывается без лишнего знака:
и модуль раскрывается без лишнего знака: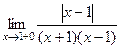 =
= 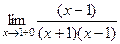 =
= 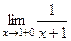 =
= 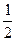 .
.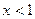 , и при раскрытии модуля знак минус:
, и при раскрытии модуля знак минус: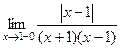 =
= 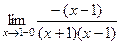 =
= 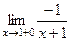 =
= 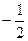 .
.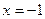 .
.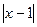 и
и 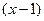 раскрываются одинаково, и равны 2 и
раскрываются одинаково, и равны 2 и 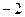 . А отличие в том, какого знака бесконечно-малая
. А отличие в том, какого знака бесконечно-малая 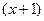 в знаменателе.
в знаменателе.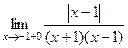 =
= 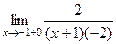 =
= 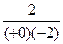 =
= 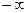 .
.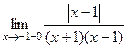 =
= 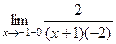 =
= 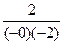 =
= 
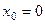 для
для 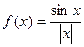 .
.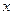 , так чтобы избавиться от синуса в выражении.
, так чтобы избавиться от синуса в выражении.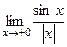 =
= 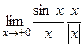 =
= 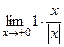 =
= 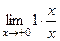 = 1.
= 1.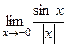 =
= 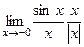 =
= 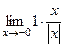 =
= 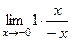 =
= 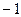 .
.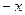 . Получились различные числа. Разрыв 1-го рода.
. Получились различные числа. Разрыв 1-го рода.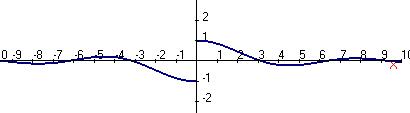
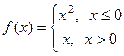 .
.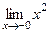 = 0.
= 0. 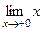 = 0. Кроме того,
= 0. Кроме того, 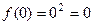 .
.
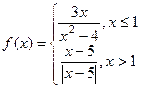 .
.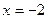 и
и 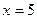 . Точка
. Точка 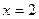 не должна рассматриваться, т.к. правее 1 уже действует другая ветвь функции.
не должна рассматриваться, т.к. правее 1 уже действует другая ветвь функции.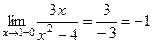 ,
, 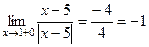 . Кроме того, значение в точке 1 тоже существует и равно
. Кроме того, значение в точке 1 тоже существует и равно 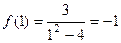 .
.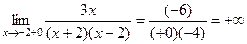 .
. 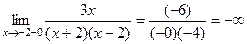 .
. 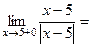
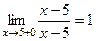 ,
, 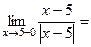
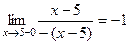 .
.
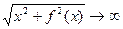 то
то 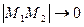 .
.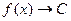 ,
, 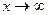 , то асимптота горизонтальная, эта ситуация имеет место, когда
, то асимптота горизонтальная, эта ситуация имеет место, когда 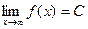 .
.
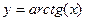 две односторонние горизонтальные асимптоты:
две односторонние горизонтальные асимптоты: 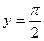 и
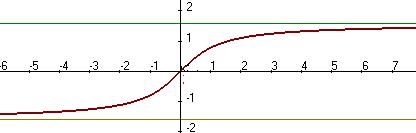
и 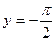 .
.
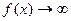 ,
, 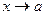 , то асимптота вертикальная (это соответствует разрыву 2 рода,
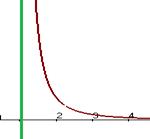
, то асимптота вертикальная (это соответствует разрыву 2 рода, 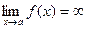 ).
).
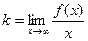 и
и 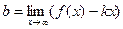 .
.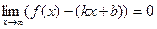 .
.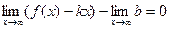 , то есть
, то есть 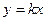 , параллельную асимптоте
, параллельную асимптоте 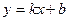 .
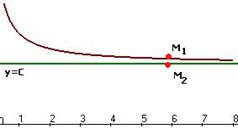
.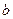 . Отрезок, соответствующий этому расстоянию, отмечен красным на чертеже.
. Отрезок, соответствующий этому расстоянию, отмечен красным на чертеже.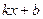 , неограниченно возрастают, и при этом разность между ними стремится к 0, то их отношение стремится к 1, то есть
, неограниченно возрастают, и при этом разность между ними стремится к 0, то их отношение стремится к 1, то есть 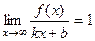 . Но ведь также очевидно, что
. Но ведь также очевидно, что 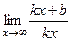 =
= 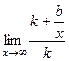 = 1.
= 1.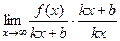 , этот предел равен 1. Однако если сократить в нём
, этот предел равен 1. Однако если сократить в нём 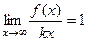 , а тогда
, а тогда 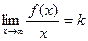 .
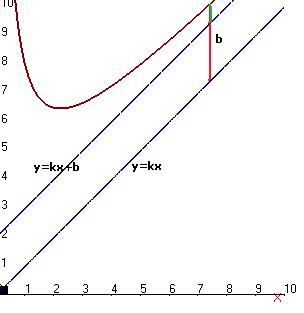
.
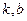 . На практике сначала надо найти
. На практике сначала надо найти 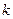 , а уже затем
, а уже затем 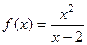 .
.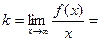
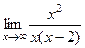 (мы просто добавили лишний
(мы просто добавили лишний 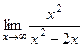 =
= 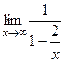 = 1. Итак,
= 1. Итак, 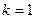 .
.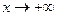 и при
и при 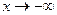 , но бывают примеры, в которых по-разному, то есть на правой и левой полуплоскости могут быть разные асимптоты.
, но бывают примеры, в которых по-разному, то есть на правой и левой полуплоскости могут быть разные асимптоты.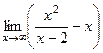 =
= 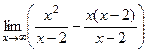 =
= 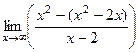 =
= 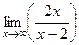 =
= 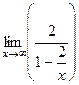 = 2.
= 2.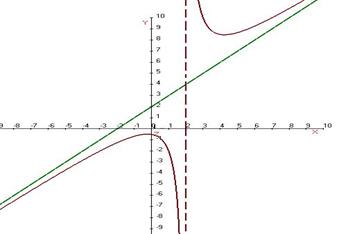
 .
.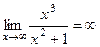 , предел не константа С.
, предел не константа С.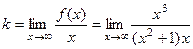 =
= 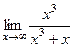 = 1.
= 1.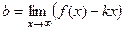 =
= 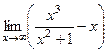 =
= 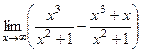 =
=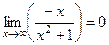 . Асимптота
. Асимптота 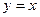 . Чертёж:
. Чертёж: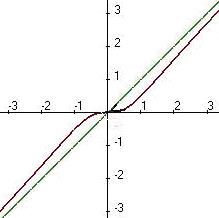
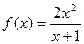 .
.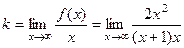 =
= 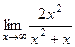 = 2. Причём этот результат не зависит от того, предел при
= 2. Причём этот результат не зависит от того, предел при 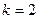 , т.е. есть наклонная асимптота типа
, т.е. есть наклонная асимптота типа 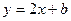 . теперь найдём
. теперь найдём 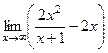 =
= 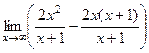 =
=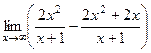 =
= 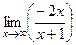 =
= 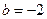 и опять же, это независимо от
и опять же, это независимо от 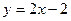 это двусторонняя асимптота.
это двусторонняя асимптота.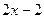 . График:
. График: 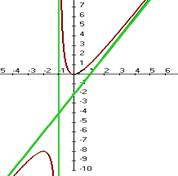
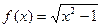 .
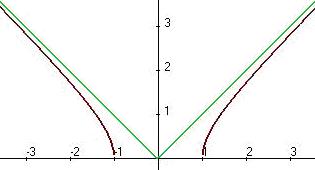
.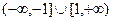 . Здесь нет знаменателя, который мог бы обращаться в 0, поэтому вертикальных асимптот нет. Функция не ограниченная при
. Здесь нет знаменателя, который мог бы обращаться в 0, поэтому вертикальных асимптот нет. Функция не ограниченная при 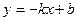 на левой. А вот двусторонняя асимптота здесь никак не могла бы быть, ведь график симметричен относительно вертикальной оси, т.к. функция чётная.
на левой. А вот двусторонняя асимптота здесь никак не могла бы быть, ведь график симметричен относительно вертикальной оси, т.к. функция чётная.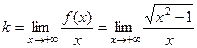 =
= 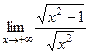 =
= 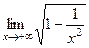 = 1.
= 1.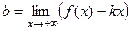 =
= 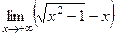 =
= 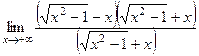
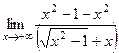 =
= 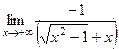 =
= 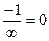 .
.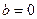 , на правой полуплоскости асимптота
, на правой полуплоскости асимптота 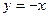 .
.
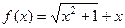 .
.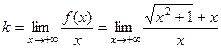 =
= 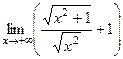 =
= 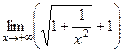 =
= 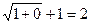 .
.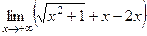 =
= 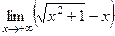 =
=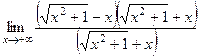 =
= 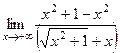 =
= 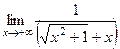 = 0.
= 0.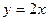 .
.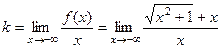 =
= 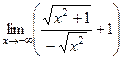 =
=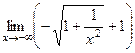 =
= 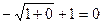 .
.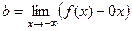 =
= 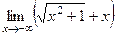 =
= 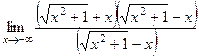
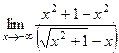 =
= 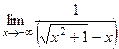 но так как
но так как 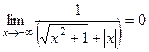 . Итак, на левой полуплоскости
. Итак, на левой полуплоскости 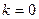 ,
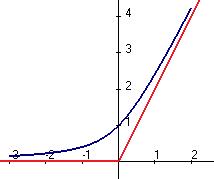
, 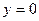 .
.
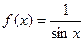 .
.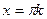 .
.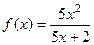 .
.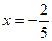 . Наклонная:
. Наклонная: 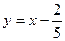 .
.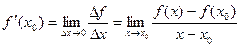 =
= 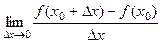

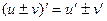 .
. 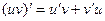 .
. 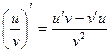 .
.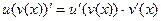 .
. 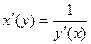
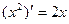 .
.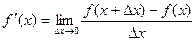 для этой функции надо записать так:
для этой функции надо записать так: 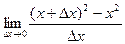
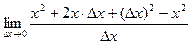 =
= 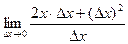 =
= 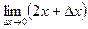 =
= 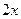 . Итак,
. Итак, 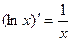 . Решение.
. Решение. 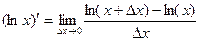 =
=  =
= 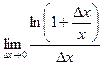 Так как следующие бесконечно малые эквивалентны:
Так как следующие бесконечно малые эквивалентны: 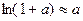 то получим, заменяя на эквивалентную:
то получим, заменяя на эквивалентную: 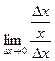 =
= 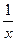 .
.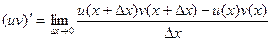
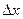 и по u, и по v. Добавим и вычтем такое слагаемое, в котором сдвиг по одной функции есть, а по второй нет:
и по u, и по v. Добавим и вычтем такое слагаемое, в котором сдвиг по одной функции есть, а по второй нет: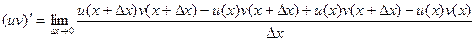 теперь слагаемых стало 4, но зато их можно сгруппировать по два, и даже разбить на две дроби, так, что дельта прибавляется только на одном из мест.
теперь слагаемых стало 4, но зато их можно сгруппировать по два, и даже разбить на две дроби, так, что дельта прибавляется только на одном из мест.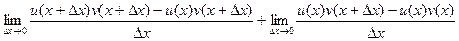
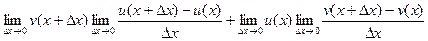
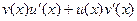 . Итак,
. Итак, 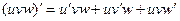 .
.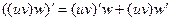 =
= 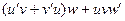 , что и приводит к
, что и приводит к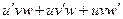 .
.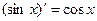 .
.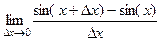 =
= 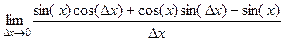 =
=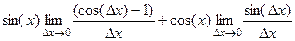 =
=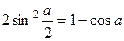 :
: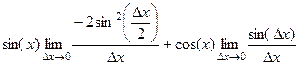 =
=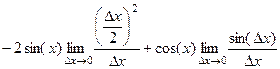 =
=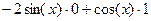 =
= 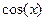 .
.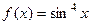 . Б)
. Б) 
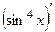 =
= 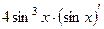 =
= 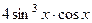 .
.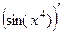 =
= 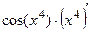 =
= 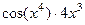 .
.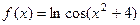 .
.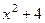 , затем вычисляется косинус, а от этого выражения зависит логарифм.
, затем вычисляется косинус, а от этого выражения зависит логарифм.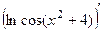 =
= 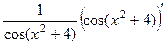 =
= 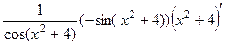 =
= 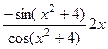 , что можно записать в виде
, что можно записать в виде 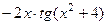 .
. 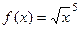 .
.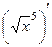 =
=  =
= 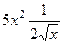 =
= 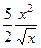 =
= 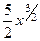 .
.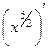 =
= 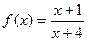 .
. 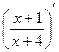 =
= 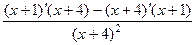 =
=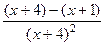 =
= 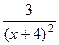 , что можно записать в виде
, что можно записать в виде 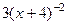 .
. 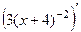 =
= 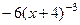 =
= 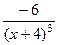 .
.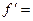
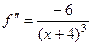 .
.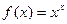 .
. 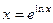 . Тогда
. Тогда 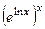 =
= 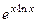 .
.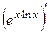 =
= 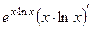 =
= 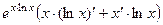 =
=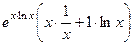 а теперь можем заменить обратно
а теперь можем заменить обратно 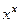 .
.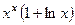 .
.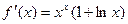 .
.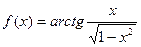 . Найти
. Найти 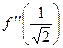 .
.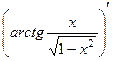 =
= 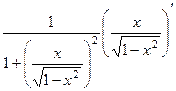 =
= 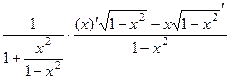 =
= =
=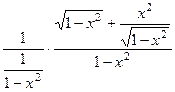 =
= 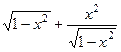 =
= 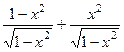 =
=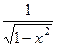 . Итак,
. Итак, 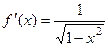 .
.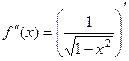 =
= 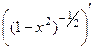 =
= 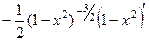 =
=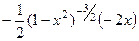 =
= 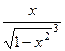 .
. 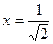 .
.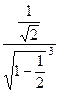 =
= 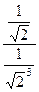 =
= 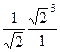 =
= 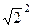 = 2.
= 2. ,
, 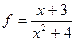 .
. 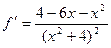
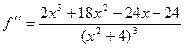
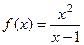 и
и 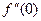 .
. =
= 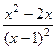 .
.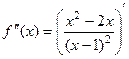 =
= 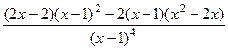 =
=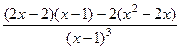 =
= 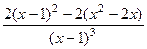 =
=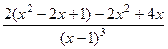 =
= 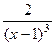 .
. 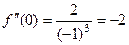 .
. 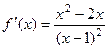 ,
, 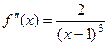 ,
, 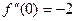 .
.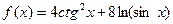 .
.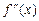 ,
, 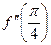 .
.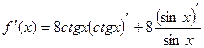 =
= 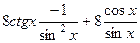 =
=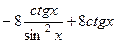 =
=  =
= 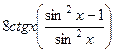 =
=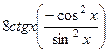 =
= 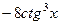 .
.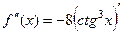 =
= 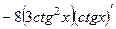 =
= 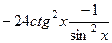 =
= =
= 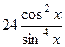 .
.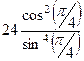 =
= 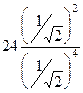 =
= 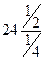 = 48.
= 48.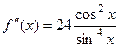 .
. 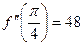 .
. , если функция
, если функция 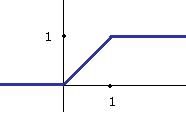
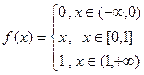
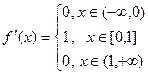
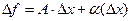
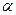 - бесконечно малая более высокого порядка, чем 1-й.
- бесконечно малая более высокого порядка, чем 1-й.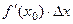 , называется дифференциалом функции
, называется дифференциалом функции 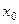 .
.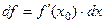 .
. 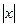 не дифф. в нуле. Нет общей касательной для двух частей графика, правой и левой. Какую бы прямую мы ни провели через (0,0), она не будет касательной к графику функции. Если наклон +450 то есть
не дифф. в нуле. Нет общей касательной для двух частей графика, правой и левой. Какую бы прямую мы ни провели через (0,0), она не будет касательной к графику функции. Если наклон +450 то есть 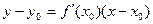 .
. 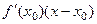 =
= 


