Правило двух шестиугольников

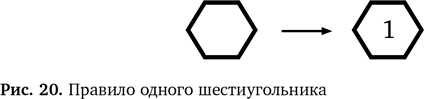
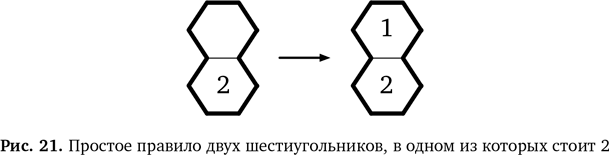
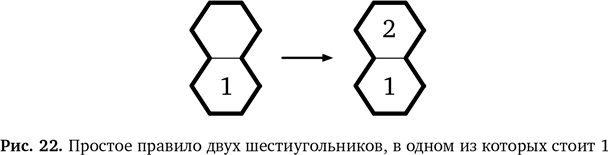
Теперь выведем еще одно новое правило для областей, состоящих из двух шестиугольников. Мы видели, что если есть область из двух шестиугольников и в одном стоит 2, то во второй нужно поставить 1 (рис. 21).

Мы вправе рассматривать это как обобщенное правило из конкретного примера нашей головоломки. Не важно, в каком шестиугольнике стоит 2, — логика не меняется. Даже если картинку перевернуть, правило останется прежним. Это правило применимо и к шестиугольникам, соприкасающимся по диагонали в любом направлении. Но обобщение можно продолжить. По той же логике, если в области из двух шестиугольников в одном уже стоит 1, в другой нужно поставить 2. Это показано на рис. 22.

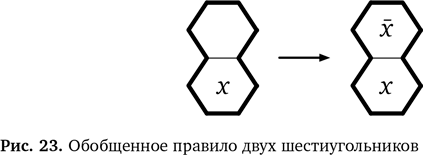
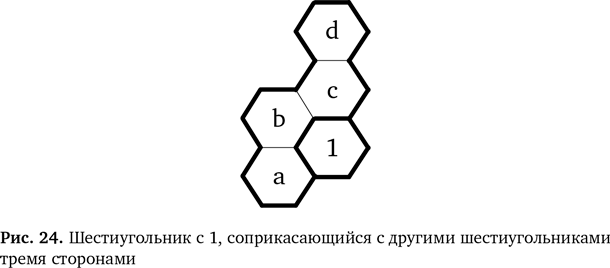
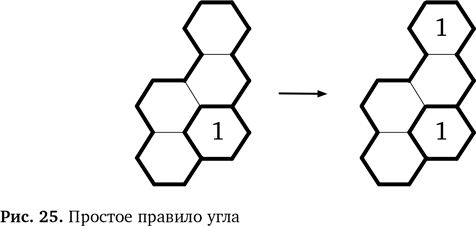
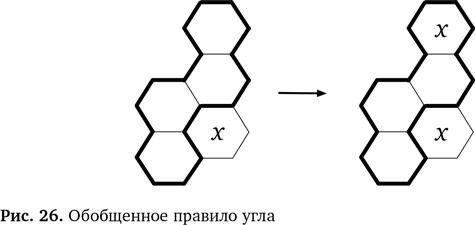
Объединив два эти отдельные правила, мы получаем полное обобщенное правило:

4. ЕСЛИ один шестиугольник в области из двух содержит 1 или 2,
ТО в другом шестиугольнике будет второе число из этих двух.

Правило можно представить в виде схемы, где x будет обозначать любое число (точно так же, как математики используют x и y для обозначения переменных в алгебре).

В одном случае x заменяет 1, а в другом — 2, но замена остается неизменной в рамках одного примера. Схема правила приведена на рис. 23. На схеме x обозначает другое число. То есть если x — это 1, то x — это 2 и если x — это 2, то x — 1. Это правило подходит для области из двух шестиугольников, повернутой в любую сторону, и не важно, какое число стоит наверху, а какое — внизу. Схема превращается в одно из изначальных правил (и их схем), если заменить x на 1 или 2. Так мы начали изобретать своего рода математические обозначения, которые используются с той же целью, что и символы в математике. Они дают возможность говорить о вещах с большой точностью, и это важно, так как по мере усложнения правил надо стараться избегать возможных ошибок.

Вместо того чтобы выводить новые факты из заданных фактов, используя исходные правила решения головоломки, мы теперь выводим новые, «более крупные» правила с учетом исходных. Это называется производные правила логического вывода. Когда мы видим ситуацию, соответствующую образцу из какого-то нового правила, мы уже не думаем, почему оно верно, а просто применяем его. Мы абстрагировались от обоснования, стоящего за правилом.

Правило угла

Давайте рассмотрим последний пример создания более общего правила на базе нашего для решения простой головоломки. Оказывается, он весьма полезен. Мы поняли, куда поставить 1 в области из четырех шестиугольников в нижнем углу. Это было возможно, потому что в прилегающей области уже стояла 1, устроившаяся в углу, как показано на рис. 24.

Единицу нужно поставить в позицию a, b, c или d (рис. 24). Однако в соответствии со вторым правилом головоломки рядом не должна находится ячейка с 1. Значит, позиции b и с исключаются. Остается только позиция d, и только туда получается поставить 1. Мы можем изобразить этот этап в виде схемы для правила замены (рис. 25).

Конечно, в любых пустых шестиугольниках уже могут стоять числа, но правило остается справедливым — это еще один способ обобщить наше новое правило. Кроме того, число, которое мы используем при сопоставлении с образцом, необязательно должно быть 1. Это может быть любое другое число в рамках достаточно большой области. Если мы опять поставим x на место любого возможного числа, то наше правило становится обобщенным вариантом (рис. 26).

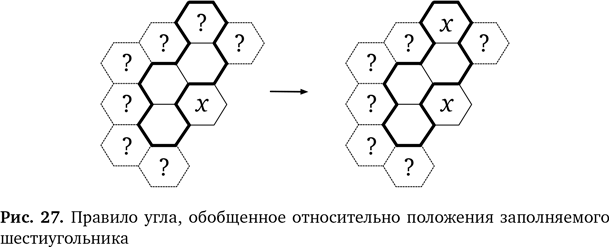
Мы даже можем продолжить обобщение нашего правила. Область, которую мы заполняем, не должна иметь заданную форму. Следующий шестиугольник может стоять в любой позиции у дальнего края более крупной области — везде, где он связан с угловым шестиугольником, но не касается его. В варианте правила угла на рис. 27 мы использовали вопросительные знаки, которые показывают возможные положения этого шестиугольника.

Получаем обобщенное правило:

5. ЕСЛИ шестиугольник соседствует с областью из четырех шестиугольников и только три из четырех соприкасаются с ним, ТО в четвертом будет стоять то же число, что и в указанном вначале шестиугольнике.

Как и в предыдущих случаях, правило применимо при любом положении схемы — перевернутом, горизонтальном, под углом или отраженном. Возможно, вы найдете больше способов обобщить правило.

Итак, сейчас у вас есть вышеприведенное общее правило. Если в головоломке вы увидите ситуацию, сопоставимую с образцом, правило можно применить. Вставьте пропущенное число, которое соответствует x.

Записываем правила

Большинство при решении головоломок не записывают правила, которые они выводят и используют. Люди просто запоминают сработавший метод и, особенно не задумываясь, по возможности применяют его. Однако специалисты по информатике любят записывать такое. Зачем это делать? Примерно по тем же причинам, что и записывать алгоритмы. Их можно использовать, например, чтобы научить других разгадывать головоломки (как это сделали мы), и тогда им не придется проходить весь этот путь с самого начала. Правила можно использовать, чтобы научить компьютер разгадывать головоломки. Кроме того, это делается ради точности. Довольно часто возникают ложные воспоминания о сработавших правилах, или мы можем выучить их, не до конца уловив детали. В любом случае в результате правило может использоваться неверно или в новой ситуации, которой оно не очень соответствует. Если записать все точно, то мы избежим такого рода ошибок.

Но здесь уже не получится использовать рисунки, как сейчас. В информатике для записи правил используют математические обозначения (формальную логику). Языки для описания этой логики немного похожи на языки программирования, но при этом они очень гибкие. Их большое преимущество состоит в том, что их легко обработать на компьютере, и затем на их основе компьютер может строить логические рассуждения. Так логика становится основой для компьютерных программ, которые позволяют решать головоломки.

Многие системы искусственного интеллекта основаны на идее использования порождающего правила. Вместо того чтобы рисовать схемы, мы пишем правила в следующем виде:

 

ЕСЛИ <какая-то ситуация> ТО <действие, которое надо выполнить>

 

Список таких правил представляет собой программу. Если правило работает, то компьютер может выполнить действие. Если совпадают несколько правил, он выбирает любое, и все повторяется снова и снова. Такой подход обеспечивает новую парадигму для создания программ и позволяет совершенно по-другому увидеть их сущность. Это не просто последовательность команд для выполнения, о которой мы говорили до сего момента, а новый тип мышления.

Все лучше осваивая искусство решения головоломок, мы не просто используем логическое мышление, а сопоставляем с образцом текущую ситуацию, чтобы узнать, какое правило нужно применить. Программа, основанная на порождающих правилах, делает похожее сопоставление с образцом. Это простое вычислительное мышление.

Когда мы записываем правила для создания программы, обобщение идет рука об руку с абстрагированием. Мы скрываем подробности, касающиеся других частей головоломки, чтобы было легче продумывать, как шире обобщить правила. На схеме, иллюстрирующей наше последнее правило, мы использовали несколько абстракций, чтобы описать, как осуществлять сопоставление с образцом. Например, переменная x — это абстракция. Мы абстрагируемся от конкретного числа (то есть опускаем подробности) — правило применимо независимо от числа. Кроме того, мы используем знак вопроса в качестве другой переменной, чтобы абстрагироваться от конкретного положения четвертого шестиугольника в нашем представлении правила. Подобным образом мы абстрагируемся от ориентации схемы — ее можно как угодно вращать или отражать, но она будет соответствовать решаемой головоломке.

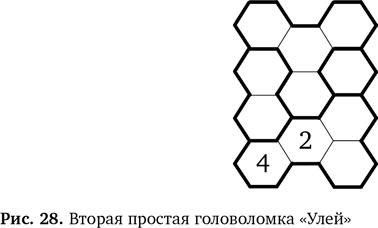
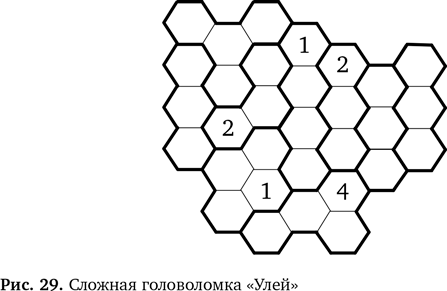
Другие головоломки

Еще один простой «Улей»

На рис. 28 представлена новая головоломка. Посмотрите, можно ли использовать приведенные выше правила для ее решения. В процессе разгадывания вы найдете новые правила. Если ни одно из выведенных ранее правил не подойдет, возможно, стоит вернуться к исходным. Помните, что по второму правилу два одинаковых числа не могут находиться рядом. Ответ приведен в конце главы.

Головоломка посложнее

На рис. 29 показана еще одна головоломка, значительно больше и сложнее. Решая ее, выводите новые правила — те, что пригодятся при решении этой головоломки, и те, что могут пригодиться в будущем.

СОВЕТ. Когда будете искать новое правило, обратите внимание на то, что происходит, когда области из трех шестиугольников граничат друг с другом.

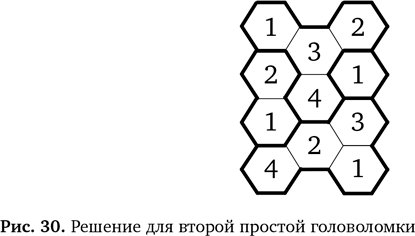
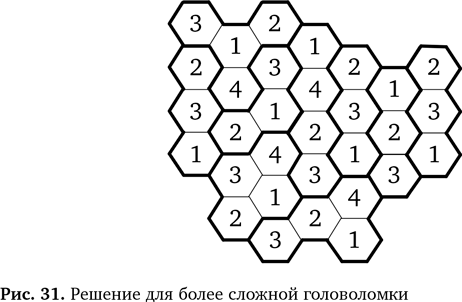
Логическое мышление и опыт

Важность логики

Какую роль логическое мышление играет в информатике? Центральную. Работа компьютеров основана на логике, а значит, чтобы программировать их, давать им указания, нужно мыслить логически. В противном случае вы с большой вероятностью ошибетесь.

Логическое мышление — один из ключевых компонентов вычислительного мышления, которое проходит через все его аспекты, и не важно, какая стоит задача — создавать алгоритмы или оценивать их. Программистам необходимо мыслить логически, когда они разрабатывают новую программу, переделывают уже существующую под новые задачи, ищут дефекты программного кода или проводят иную оценку.

В информатике используются очень простые и точные языки математической логики. Как и наши головоломки, эти языки имеют набор правил, называемых аксиомами. Наши два исходных правила головоломки являются для нее аксиомами. Так же, как и мы, математики выводят из аксиом правила более высокого уровня, что позволяет продвигаться в рассуждениях большими шагами.

Такие логические элементы формируют основу языков программирования и определяют, что означает каждая их конструкция. Поэтому люди, создающие программы, тоже должны рассуждать логически. Поскольку в основе языков программирования лежит логика, мы можем использовать логическое мышление, чтобы рассуждать о возможностях наших программ. Таким образом даже можно убедиться в правильности их работы. Для этого действия программы описывают на языке логики. Затем с помощью логических рассуждений подтверждают, что программа дает именно задуманный эффект.

Мы также увидели, что программисты изобрели способы приравнять логические правила к собственно программам — это называется логическое программирование. Чтобы написать такую программу, надо разработать правила, на основании которых можно произвести определенные вычисления. Правила для нашей головоломки, записанные на языке логического программирования, могли бы стать программой для решения задач. И какой бы язык программирования вы ни использовали, логическое мышление придется применять обязательно.

Специалисты за работой

Чем больше у нас опыта в разгадывании головоломок, тем больше правил накапливается в уме и тем быстрее и легче мы решаем новые задачи. Именно так гроссмейстеры играют в шахматы. Они видят в текущих позициях ситуации, похожие на те, что им уже встречались, и делают ход, подсказанный опытом. Это позволяет не перебирать огромное количество ходов наперед, что у человека происходит медленно и порой с ошибками. Компьютеры играют именно так — перебирают массу вариантов и смотрят, какие будут последствия. Люди-шахматисты играют гениально, потому что используют как логическое мышление, так и сопоставление с образцом; кроме того, у них накопилась масса неформальных правил.

Так поступают не только профессиональные шахматисты. Есть предположение, что это свойственно практически всем специалистам независимо от навыка, которым они прекрасно овладели. Например, когда пожарные успевают выбраться из горящего здания прямо перед обвалом крыши, это происходит благодаря сопоставлению с образцом, только процесс идет подсознательно. Интуиция — подсознательное сопоставление с образцом на основе богатого прошлого опыта.

Если вы хотите стать специалистом в любой области, развивайте навыки сопоставления с образцом и обобщения. Есть универсальный принцип, который позволяет овладеть любым навыком до уровня гения и стать невероятно успешным, — нужно потратить 10 000 часов на тренировки. Столько времени тратят на занятия скрипачи-виртуозы. Подобным образом самые успешные программисты (те, кто стал миллиардерами) примерно столько учились писать программы. Даже тибетские монахи, известные безмятежностью и способностью сострадать, практиковали медитацию примерно столько же времени, чтобы достичь внутреннего покоя.

Если вы хотите в совершенстве овладеть программированием, начинайте практиковать вычислительное мышление прямо сейчас. И даже если вы не собираетесь стать программистом, развивая такие навыки, как логическое мышление, обобщение, абстрагирование и сопоставление с образцом, вы добьетесь больших успехов в любой профессии. Логические головоломки — занимательный способ тренировать эти навыки, особенно если будете обдумывать процесс и записывать правила.

Ответы

На рис. 30 и 31 показаны решения для двух последних головоломок «Улей».

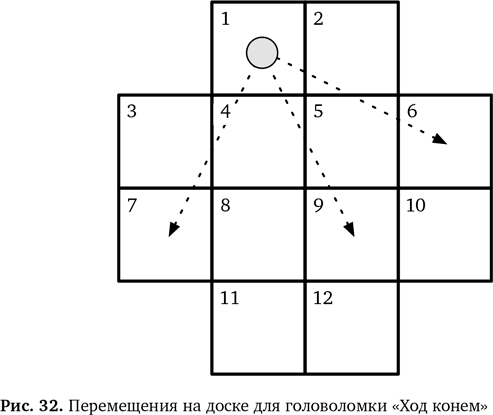
Глава 5

Головоломные маршруты

Найдите для шахматного коня способ побывать в каждой клетке на доске ровно один раз, решите проблему экскурсовода и, наконец, проведите консультацию в информационном центре для туристов. Сделайте все это как можно лучше, используя вычислительное мышление. Да, и еще помогите туристам упаковать чемоданы. Алгоритмы находятся в центре вычислительного мышления и позволяют нам решить задачу один раз — и больше не думать о ней никогда. Однако выбрать хороший способ для представления используемой информации — еще один важный аспект вычислительного мышления. Сделайте это хорошо, и составить алгоритм будет гораздо легче.

Две задачи

Задача «Ход конем»

В головоломке «Ход конем» один шахматный конь может передвигаться по небольшой доске в форме креста. Конь ходит на два поля в любом направлении, а потом на одно поле перпендикулярно этому направлению или наоборот. Он переходит на новое поле, не останавливаясь на полях между начальным и конечным, и всегда должен оставаться в пределах доски. Возможные первые ходы в головоломке показаны на рис. 32.

Вам нужно найти последовательность ходов, начиная с поля 1, чтобы конь побывал на всех полях ровно один раз и вернулся в исходную точку.

Решите это!

Попробуйте решить задачу «Ход конем», замерив, сколько времени у вас уйдет. При этом недостаточно, чтобы конь прошел заданный путь. Необходимо найти алгоритмическое решение, а не просто двигать фигуру по доске. Для этого нужно записать серию перемещений, которые приведут к ответу. То есть придется применить алгоритмическое мышление и вывести алгоритм для решения головоломки. Этот алгоритм можно записать в виде списка номеров, присвоенных полям, на которые ходит конь, в порядке прохождения. Или же записать алгоритм как серию команд вроде «перейти с поля 1 на поле 9». Решать вам.

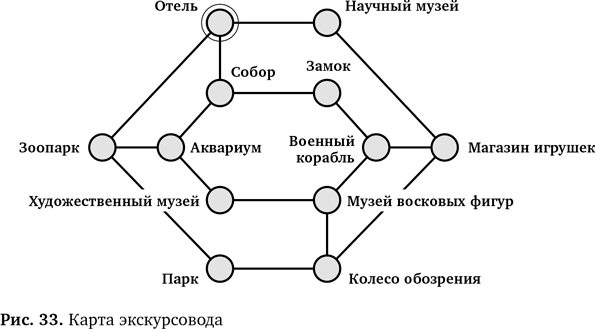
Как только у вас появится работающий алгоритм, оцените его: проверьте, действительно ли работает это решение, опробовав его на практике. Следуйте собственным инструкциям, отмечая клетки по мере того, как их обходит конь. Таким образом вы сможете гарантировать, что он не нарушает правила и посещает каждую клетку ровно один раз. Если головоломка решена, прекрасно! Если нет, не беспокойтесь — ниже мы посмотрим, как облегчить эту задачу. Но сначала давайте попробуем решить задачу полегче.

Задача экскурсовода

Вы экскурсовод и работаете в отеле. Туристы из вашего отеля хотят отправиться на дневную экскурсию и посетить все достопримечательности города. Вам дали карту (рис. 33), на которой показано расположение достопримечательностей и указано, как добраться до них на метро.

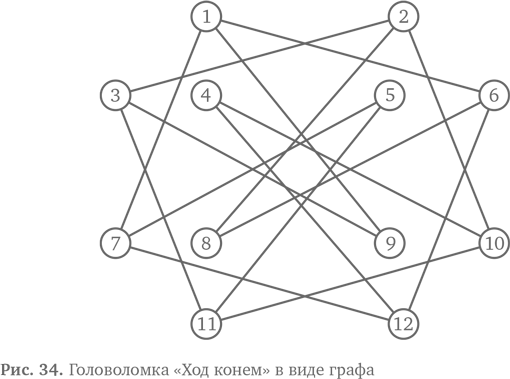
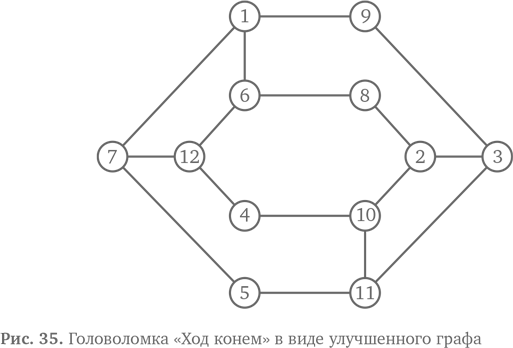
Вам нужно составить маршрут, который начнется в отеле и позволит показать вашей группе все интересные места. Туристы прибыли в город всего на день и не хотят терять времени. Очевидно, они будут недовольны, если придется два раза проходить через одно и то же место. Также очевидно, что вечером они хотят оказаться в отеле.

Как и в случае с «Ходом конем», задача — найти алгоритмическое решение. Убедитесь, что ваше решение действительно работает. Сколько времени у вас ушло? Оказалась ли эта задача легче, чем предыдущая (то есть вы решили ее быстрее)?

Что необходимо?

Почему важно проверить, верно ли ваше решение? Ну конечно, вам не хотелось бы отправиться на экскурсию и в конце дня обнаружить, что вы пропустили важную достопримечательность. Кому хочется разбираться с недовольными туристами!

Чтобы проверить алгоритм, нужно провести процедуру, которую в информатике называют трассировкой. Это всего лишь означает, что сначала вы проходите все этапы алгоритма на бумаге. Вероятно, вы так и сделали, проверяя решения для «Хода конем». Для задачи, решаемой экскурсоводом, можно нарисовать маршрут на карте и, следуя инструкциям, помечать каждое посещенное место.

Конечно же, настоящий экскурсовод не удовлетворяется проверкой маршрута на бумаге. Он пойдет и проверит все в реальных условиях. Вы бы тоже пошли и проверили все сами, но, если сначала выполнить проверку на бумаге, это сэкономит массу времени. Программисты поступают точно так же. Сначала они проверяют, как программа работает на бумаге (трассировка), а потом испытывают ее в реальных условиях — проводят тестирование. Так же, как в случае с вашей задачей, программисты делают это, чтобы гарантировать бесперебойную работу программ.

Вообще, процедуру оценки можно сделать точнее. Для этого надо определить, какие именно особенности выполнения задачи важны, чтобы получить правильное решение. Если мы запишем список этих необходимых вещей, то сможем проверить, соответствует ли им найденное решение. В информатике такие особенности называются требованиями.

Для задачи экскурсовода нужно проверить, удовлетворяет ли итог следующим требованиям.

1. Экскурсия начинается в отеле.

2. Туристы посещают все достопримечательности.

3. Они не проходят одно и то же место дважды.

4. Экскурсия завершается в отеле.

Вернитесь назад и запишите список требований к головоломке «Ход конем». Видите что-нибудь похожее? Мы вернемся к этому ниже.

Почему это легко?

Возможно, вам показалось, что задача «Ход конем» сложнее, но на деле это не обязательно так. Решить ее будет очень легко, если использовать еще некоторые приемы из компьютерного мышления.

Почему задача экскурсовода легкая? Карта метро дает важную информацию, незначительные детали опущены. Это хороший пример абстракции — решение легко увидеть. Без карты было бы сложнее, даже если бы мы знали, где что находится. Карта метро — особый способ предоставления информации. Это особый вид схемы под названием граф. В информатике под графом подразумевают несколько кружков (мы называем их вершинами графа) и линий, которые их объединяют (ребра графа). Вершины и ребра представляют те аспекты данных, которые нас интересуют. Ребра показывают, какие вершины объединены таким образом, что это важно для решения нашей задачи. Туристические достопримечательности, вероятно, соединены автомобильными дорогами, но по-другому. В этом случае граф пути был бы другим — и он понадобился бы нам, если бы мы организовывали автобусный тур!

Это не важно!

Нас интересует, какие у нас есть достопримечательности (наши вершины) и какие из них соединены друг с другом линиями метро (наши ребра). Другие особенности этих мест нас не интересуют, поэтому мы их игнорируем. Мы опускаем их точное расположение, расстояние друг от друга, соединения автодорог и многие другие вещи, которые не относятся к нашей задаче — понять, как объехать все это на метро. Граф — это абстракция реального города. Мы спрятали все лишние детали, не нужные для построения графа. Здесь отражена только важная информация. Поэтому нам легко увидеть действительно необходимое для решения. Это хорошее представление текущей задачи.

Упрощаем

Графы часто используются, чтобы представить информацию о связях между объектами. Это маршруты на автобусных остановках, карты поездов и метро. Граф — очень хорошее представление в ситуации, когда нужно проложить маршрут из одного места в другое, как в нашем случае. Упрощенный граф облегчает составление маршрута по сравнению с максимально точной картой, где трудно выделить нужную информацию среди многочисленных подробностей.

Циклы

В информатике есть особое название для обхода графа, когда вы посещаете каждую вершину ровно один раз и возвращаетесь в начало. Это называется гамильтонов цикл — по имени ирландского физика Уильяма Роуэна Гамильтона. Он изобрел головоломку, по условиям которой нужно было обойти все углы додекаэдра, проходя по его граням.

Одно решение на двоих

Возвращаемся к началу

Возможно, вы уже заметили, что головоломка «Ход конем» и задача экскурсовода очень похожи друг на друга. Если вы записали требования для «Хода конем», то, вероятно, увидели полное совпадение.

1. Тур начинается в заданной точке.

2. Необходимо посетить все точки.

3. Нельзя проходить уже посещенную точку.

4. Необходимо закончить в начальной точке.

В обоих задачах вас просят найти гамильтонов цикл! Таким образом, мы использовали прием из вычислительного мышления. Мы обобщили обе задачи, чтобы они стали одинаковыми, и сделали это с помощью сопоставления с образцом, увидев важнейшие сходные черты. При этом мы абстрагировались от деталей, таких как отели и туристические достопримечательности или необходимость ходить конем или ехать по линиям метро.

Итак, задача экскурсовода оказалась легкой, потому что мы представили ее в виде графа. Так почему бы нам не сделать то же самое и с задачей «Ход конем»?

Для этого нужно абстрагироваться в большей степени. Чтобы это сделать, необходимо осознать две вещи. Во-первых, не важно, как выглядит доска. Не важно, что поля — это квадраты. Их форма и размер могли бы быть абсолютно любыми. Давайте нарисуем каждое поле в виде кружочка — так же, как достопримечательности изображены на карте метро. Это просто вершины графа.

Во-вторых, какие поля на самом деле находятся рядом друг с другом — тоже не очень важно. Единственное, что имеет значение, — между какими полями конь перемещается. Поэтому давайте соединим линиями любые два кружка, между которыми можно сделать ход. Подобным образом карта метро показывает, между какими достопримечательностями можно переместиться на метро. Это ребра графа.

Создаем граф

Чтобы сделать граф для головоломки «Ход конем», переходите с поля на поле и по мере продвижения рисуйте кружки и линии (вершины и ребра). Если четко выстроить путь, вы ничего не пропустите. Начните с поля 1. Нарисуйте кружок и пометьте его цифрой «1». Теперь с поля 1 можно перейти на поле 9 — значит нужно нарисовать еще один кружок, обозначить его как «9» и соединить их линиями. С поля 9 перейдите на поле 3 и нарисуйте еще один кружок, который пометьте «3» и соедините его линией с кружком 9.

Продолжайте так делать, пока не вернетесь к уже нарисованному кружку. Теперь отойдите на ход назад и попробуйте из этой точки пойти другой дорогой. Если других вариантов, которые вы еще не обозначили, больше нет, вернитесь еще на один ход и попробуйте оттуда. Продолжайте делать так до тех пор, пока не проведете эту операцию (она называется поиск с возвращением) до поля 1 и у вас не кончатся варианты. В итоге вы получите схему.

Заметим, что из трех внутренних кружков возможны только два хода, а значит, на завершенной схеме на каждую из этих вершин придется по два ребра (линии). С других полей можно сделать три разных хода, поэтому у их вершин будет по три ребра.

Идем вглубь

Способ исследования всех возможных ходов с целью нарисовать граф называется поиском в глубину: мы исследуем пути до самого конца, например продвигаясь через 1 — 9 — 3 — 11... до конца, потом сохраняем этот путь и пробуем другие. Альтернативный вариант (под названием поиск в ширину) подразумевает рисование всех ребер, исходящих из вершины, и всех вершин, к которым они ведут, перед перемещением к новой вершине. Используя этот метод, мы могли бы нарисовать все ребра из вершины 9, потом все ребра из вершины 6 — и так далее. Это два разных алгоритма для исчерпывающего исследования графа — два разных алгоритма обхода графа. Как только вы осознаете, что задачу можно представить в виде графа, то используйте любой из этих алгоритмов в качестве упорядоченного способа исследования графа и, соответственно, задачи.

Чистота и порядок

Если ваш рисунок получился немного беспорядочным из-за наезжающих друг на друга линий, как показано на рис. 34, можно перерисовать его начисто, чтобы линии не пересекались. В этом случае используйте два связанных шестиугольника — один внутри другого, как на рис. 35.

Когда вы аккуратно начертите граф, попробуйте снова решить задачу «Ход конем». Начните с вершины 1 и следуйте линиям, отмечая вершины, которые проходите. Теперь найти решение должно быть довольно легко.

Одна задача, одно решение

Теперь внимательно посмотрите на чистый вариант графа. Мы перечертили его, не меняя ребер и вершин, и он выглядит в точности как схема метро. Единственная разница — в обозначениях вершин. Цифры вместо названий.

Теперь видно, что эти задачи можно обобщить и что они не просто похожи, но в точности одинаковы. Если у вас есть решение для одной задачи (алгоритм, позволяющий найти ответ), значит, есть и для другой! Все, что нужно сделать, — поменять обозначения. Обобщенная версия алгоритма подойдет для обеих головоломок, и ничего не придется делать заново.

Сопоставление схем

На рис. 36 показано, как поменять обозначения на графе одной из наших задач, чтобы он подошел для другой. Еще на нем видно, как перевести решение одной задачи в решение другой. Обозначение каждого шага в алгоритме для одной из задач нужно заменить на соответствующее в другой.

Итак, если мы нашли следующее решение для задачи экскурсовода:

1. Отель.

2. Научный музей.

3. Магазин игрушек

4. Колесо обозрения.

5. Парк.

6. Зоопарк.

7. Аквариум.

8. Художественный музей.

9. Музей восковых фигур.

10. Военный корабль.

11. Замок.

12. Собор.

13. Отель,

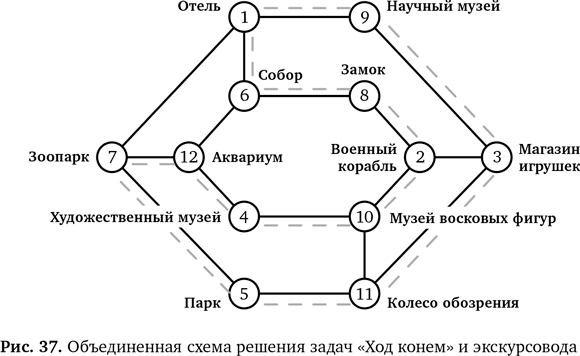
то, используя таблицу, сразу же найдем решение для «Хода конем»:

1. Поле 1.

2. Поле 9.

3. Поле 3.

4. Поле 11.

5. Поле 5.

6. Поле 7.

7. Поле 12.

8. Поле 4.

9. Поле 10.

10. Поле 2.

11. Поле 8.

12. Поле 6.

13. Поле 1.

Эта таблица — еще один вид представления информации или структуры данных в виде таблицы поиска. С ее помощью вы легко найдете эквивалент поля из «Хода конем» в списке достопримечательностей из задачи для экскурсовода. Но стоит заметить, что искать поле, соответствующее достопримечательности, не очень удобно. Было бы гораздо лучше, если бы достопримечательности стояли в алфавитном порядке.

Схема для обеих задач

Схема на рис. 37 — еще одно представление той же информации, полученное методом наложения. Также она показывает единое решение (для обеих задач). Конечно, поскольку решений может быть много, вы можете прийти к какому-то другому, но и тогда оно подойдет для обеих задач.

Итак — вероятно, это удивит вас, — две разные вроде бы задачи оказались одинаковыми и с одним решением (после обобщения). Решив одну, вы сразу решили и другую! Это открытие происходит после выбора подходящих абстракций и подходящего представления двух задач (структура данных в виде графа).

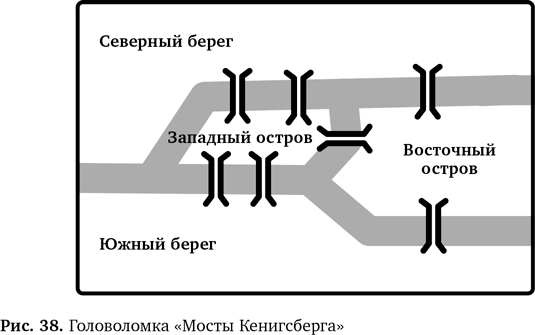
Мосты Кенигсберга

Прогулка по городу мостов

Вот еще одна головоломка, над которой стоит поразмыслить. На рис. 38 показана карта города с рекой, протекающей через него, двумя островами и семью мостами через реку.

Туристический информационный центр хотел бы опубликовать маршрут прогулки по городу (оба берега и острова), чтобы по каждому мосту нужно было пройти один раз (не больше). Маршрут должен начинаться и заканчиваться в одном месте. Вас попросили проконсультировать центр — либо предложить маршрут, либо объяснить, почему он невозможен.

Похожую задачу о мостах города Кенигсберга в XVIII веке решил математик Леонард Эйлер. В своем решении он впервые ввел идею графов. В итоге они стали одним из ключевых вычислительных инструментов как в математике, так и в информатике. Ученые Викторианской эпохи Чарльз Беббидж и Ада Лавлейс, написавшие первые компьютерные программы, попытались решить ее в XIX веке. Нарисуйте граф для задачи и посмотрите, сможете ли решить ее, прежде чем читать дальше.

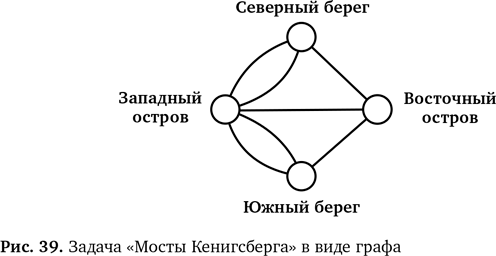
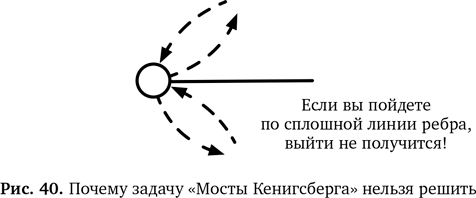
Мыслим логически

Вычислительное мышление подразумевает умение мыслить логически. Хорошее представление информации помогает в этом, потому что позволяет убрать ненужное и сосредоточиться на главном. Именно это и обнаружил Леонард Эйлер, когда решал задачу «Мосты Кенигсберга» и пришел к мысли нарисовать граф (рис. 39). Граф помог ему увидеть задачу предельно ясно.

Глядя на граф, Эйлер осознал, что найти ответ невозможно. Почему? Подходящий маршрут должен затронуть все вершины и обойти все ребра, но только один раз (поскольку ребра — это мосты, а нам сказали, что по каждому мосту можно пройти один раз). Давайте предположим, что такой маршрут существует, и, чтобы его показать, нарисуем пунктирные линии со стрелками вдоль ребер. Все ребра должны входить в маршрут, а значит, все они должны совпасть с пунктирными стрелками. Возьмем вершину на этом маршруте, как показано на рис. 40. На каждую пунктирную стрелку, направленную от нее, должна приходиться пунктирная стрелка, направленная к ней. В противном случае маршрут зайдет в тупик — когда пойдет по лишнему ребру, над которым не будет пунктирной стрелки. Из этого тупика не получится выйти без возвращения на уже пересеченный мост. То же относится и к любой вершине. Поэтому, чтобы искомый маршрут был возможен, у всех вершин должно быть четное число связанных с ними ребер.

Все вершины на графе Кенигсберга имеют нечетное число ребер, поэтому искомый маршрут невозможен. Однако со времен Эйлера через реку построили новый мост, поэтому граф изменился. Экскурсоводам современного Калининграда живется легче.

Собираемся и путешествуем

Настоящее путешествие

Мы рассмотрели простые головоломки с поиском маршрута. Теперь возьмем задачу из реальной жизни. Представьте, что специалист по продажам каждый день настраивает навигатор, чтобы найти самый короткий путь, позволяющий по одному разу посетить несколько клиентов в разных городах и снова оказаться в офисе, не возвращаясь по собственным следам.

Такую кратчайшую дорогу можно просчитать, но вряд ли получится каждый раз делать это за разумный промежуток времени. Даже если надо побывать у 20 клиентов, нельзя гарантировать, что вы ежедневно будете находить оптимальное решение — на это потребуется слишком много времени. И дело не в том, что требуется более мощный навигатор или компьютер. Если число мест, где необходимо побывать, достаточно велико (на самом деле оно не очень-то и велико), то на поиск совершенного решения уйдет больше времени, чем прошло с момента возникновения Вселенной, — даже при наличии самого быстрого компьютера! Почему? Потому что число возможных вариантов, которые необходимо проверить, стремительно растет с появлением каждого нового города. Даже если навигатор запрограммировать на какое-то решение, нельзя гарантировать, что оно будет безупречным. Заложенный в программу способ не обеспечит кратчайшего пути. Вполне вероятно, что в программе сработает так называемый жадный алгоритм. Давайте изменим условия задачи, чтобы понять, о чем идет речь.

Пакуем чемоданы

Представьте, что вы отправляетесь в долгий отпуск, мечтая хорошо отдохнуть. Открытый чемодан лежит на кровати. Вы уже упаковали одежду и теперь собираете вещи, которые хотите взять с собой, — книги, настольные игры, пазлы, колоду карт, краски и бумагу… Все, что, по вашему мнению, поможет расслабиться. Все эти вещи разного размера. Их нужно сложить в чемодан. Как это сделать? Пробуем разные варианты. Сначала пазл, потом игральные карты, потом книга с кроссвордами — и так далее. Если у вас достаточно места, то все получится, однако, если места маловато или вы не хотите брать много чемоданов, намечается проблема.

Хорошей альтернативой будет жадный алгоритм. С его помощью не получится упаковать все максимально компактно, но порой он работает весьма хорошо. Как выбрать, что положить сначала? Исходите из жадности. Положите самый большой предмет внутрь, пусть он займет как можно больше места. Теперь положите следующий по размеру — и так далее. Если что-то не помещается, берите следующий чемодан. Обычно все получается само собой, потому что, когда у вас остаются небольшие свободные пространства, вы заполняете их небольшими предметами. Это годный эвристический алгоритм — с такими алгоритмами вы достаточно хорошо (но не безупречно) справитесь с задачей. Они не гарантируют оптимального решения.

Снова в дороге

Основная идея жадного алгоритма применима и при разработке маршрута для коммивояжера. Используя ту же идею обобщения, вы на каждом этапе выбираете ближайший к точке отправления город. При этом не всегда получается оптимальный вариант, но можно рассчитывать на хороший результат за разумное время.

Хороший, плохой, злой

Идея прокладывания маршрута между точками, которая при подходящем обобщениидает граф, возникает снова и снова при решении самых разных задач. Как только вы осознали, что это граф, в вашем распоряжении сразу оказывается много алгоритмов. Тогда некоторые задачи оказываются легкими, а другие — нерешаемыми. Однако интереснее всего те, что по мере роста масштаба задачи утрачивают рациональность решения. В этом случае необходимо правильно подать информацию и выбрать алгоритм. К примеру, важно вовремя заметить, что проблема становится сложной и лучше использовать эвристический алгоритм.

Выбор подачи информации и алгоритма может быть хорошим или плохим. Некоторые варианты подачи и алгоритмов просто красивы — их элегантность доставляет настоящее удовольствие в процессе решения задачи.

Глава 6