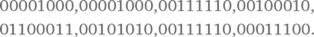Решетки и игры как изображения

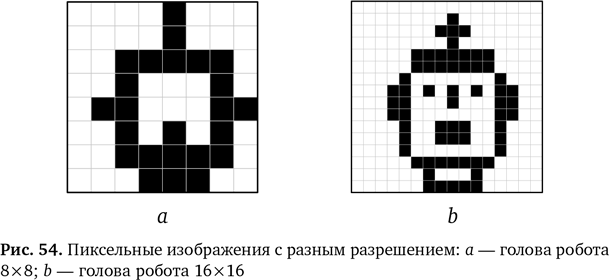
Игры как высокотехнологичная область искусства

История компьютерных игр довольно коротка, но отрасль настолько разрослась, что сегодня стоит дороже, чем киноиндустрия. Играете ли вы за тролля в Warcraft или деретесь с назойливыми свинками в Angry Birds, за этим стоят компьютерные программы, установленные в игровых приставках, ноутбуках, смартфонах и планшетах, которые мы носим с собой по всему миру. Они обеспечивают нам и развлечения, и новые способы взаимодействия с другими людьми.

Полные видеоигры можно разделить на две основные категории. Над большими играми работают многие сотни людей — программисты, дизайнеры и художники. Они используют и науку — например, в физических движках, компьютерных программах, которые моделируют физические законы виртуального мира. Эти движки определяют, как падают камни или как ткань развевается на ветру. Конечно же, здесь мы наблюдаем пример компьютерного моделирования, только оно используется скорее для развлечения, чем для исследований. Сегодня видеоигры представляют собой сплав информатики и художественного творчества. Как сказал пионер отрасли Ричард Гэриотт, это квинтэссенция высокотехнологичного искусства.

Вторая основная категория игр — независимые игры, в основном разрабатываются для смартфонов. Здесь для результата хватит небольшой группы увлеченных и творческих программистов и дизайнеров. Появление рынка приложений для смартфонов привело к взрывному росту новых идей и тем, которые можно исследовать и развить. Это особенно верно для игр, интегрированных в социальные сети (наши так называемые социальные графы), в которых все мы проводим много времени. Говорят, идея для приложения найдется у каждого, и с небольшой помощью вы сможете сами что-нибудь создать. Если вам интересно, можно взять бесплатный программный пакет из интернета, который позволит превратить ваши идеи в код для смартфона. Потом его можно скачать на свой телефон и удивить друзей.

Пиксельные картинки

В основе своей компьютерные игры строятся на компьютерной графике и изображениях (хотя можно ждать появления компьютерных игр, в которые вы будете играть в реальном мире и при этом задействовать все органы чувств!). Изображения, которые мы видим на экране, состоят из многих тысяч пикселов. Пикселы — это просто элементы картинки, маленькие точки на экране. Их яркость и цвет можно изменять, потому что они представлены в виде цифр. Если экран достаточно велик, можно создать абсолютно любое изображение, установив для пикселов определенное значение с помощью правильно подобранных чисел. Чем больше пикселов, тем выше разрешение и тем более детальное и четкое изображение мы можем получить. На рис. 54a изображена голова робота из 64 пикселов (8×8). Рисунок едва узнаваем, поскольку пикселов не хватает, чтобы показать детали. На рис. 54b — та же картинка, но пикселов уже 256 (16×16). Очевидно, что это голова робота. Если добавить еще пикселов, то есть увеличить разрешение, картинка может стать еще более подробной — например, на ней можно показать форму глаз, носа и рта.

Сам экран компьютера можно считать решеткой, и в таком случае игра — это серия изображений, которые мы контролируем (снова представление в действии).

Изображения можно создавать самыми разными способами с помощью компьютерной графики. Простые растровые методы подразумевают сохранение каждого пиксела. Нашу первую картинку можно сохранить в виде 64 цифр:

Здесь 0 означает белый пиксел, а 1 — черный пиксел. Мы создаем изображения, продвигаясь по линиям сверху вниз и быстро устанавливая значение пикселов.

Чем больше пикселов, тем яснее изображение, но и тем больше цифр необходимо сохранить, чтобы представить его. Чтобы сохранить изображение робота в более высоком разрешении, нам понадобится 256 цифр вместо всего лишь 64:

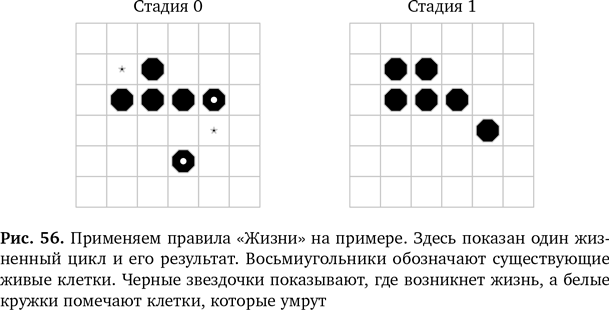
Для этих изображений мы выбираем одну из всего двух цифр на каждый пиксел — 1 или 0, поэтому у нас всего два цвета, белый и черный. Если использовать больше цифр, где каждая будет представлять свой цвет, то можно подобным образом сохранять цветные изображения.

Альтернативное представление изображения — сохранить его в виде линий и фигур, из которых оно состоит. Это так называемые векторные методы. Мы определяем начальные и конечные точки для тысяч линий и быстро рисуем их на экране. Например, чтобы нарисовать квадрат, вместо обозначения каждого пиксела в сетке вы сохраняете серию инструкций:

Линия (Север, 50)

Линия (Восток, 50)

Линия (Юг, 50)

Линия (Запад, 50)

Чтобы нарисовать изображение, мы просто выполняем инструкции. Такое представление в целом занимает гораздо меньше места, но у него есть еще одно большое преимущество. Инструкция выше позволяет нарисовать квадрат со стороной 50. Допустим, мы хотим получить изображение в 10 раз больше. В этом случае просто умножаем все значения на 10. Если же мы хотим, чтобы квадрат был в 10 раз меньше, то делим их на 10. Благодаря этому представлению мы можем увеличить изображение до любого размера, например чтобы показать его на большом экране, но без необходимости хранить еще больше данных и не теряя точности.

Вот почему представление диаграмм как в pdf-файлах занимает меньше места и выглядит одинаково хорошо, как бы вы ни увеличивали изображение. В таких файлах хранятся векторные версии. Изображение в формате jpeg требует больше памяти, чтобы сохранить картинку в более высоком разрешении, и при сохранении нужно указать, каким именно оно будет. Вот почему, приближая изображение в формате jpeg, вы видите, что все расплывается и линии становятся неровными.

С помощью векторных методов мы создаем трехмерные формы, объединяя много, порой десятки тысяч, так называемых графических примитивов — сфер, кубов, цилиндров и так далее. Различные комбинации позволяют нам создавать желаемые сложные формы.

Существуют системы, которые симулируют распределение световых лучей в искусственном мире (для этого требуется компьютерное моделирование — на сей раз чтобы показать, как источники света освещают предметы). С их помощью создают фотореалистичные изображения. Кроме того, к нашим графическим примитивам добавляют скрипты, отвечающие за сложные движения персонажей, — их часто создают, снимая движения настоящих актеров, — и таким образом фигуры будут двигаться как мы хотим. Ограничения — это объем доступных вычислительных мощностей, качество кода, который пишут кодировщики-программисты, чтобы графика выглядела еще естественнее, и воображение творческого человеческого ра­зума. Но даже простая сетка и несложные правила кодирования могут дать замечательные результаты.

Жизнь как игра

Играем в сетке

Давайте начнем с простого — с игры, в которой есть квадратная сетка и набор правил, в зависимости от которых на ней появляются и исчезают пикселы. Значение пиксела меняется и зависит от того, сколько других пикселов находится рядом. Звучит не очень интересно, правда? Но не торопитесь с выводами. Даже в этой простой игре происходит много интересного, и мы используем ее, чтобы кое-что понять о мире природы.

Игра называется «Жизнь», ее автор — математик Джон Конвей. Впервые правила игры были опубликованы в 1970 г., и впоследствии она приобрела популярность у программистов по всему миру. Правила просты, хотя Конвей приложил массу усилий, чтобы их правильно сбалансировать и гарантировать интересный игровой процесс.

Сетка представляет собой небольшой квадратный мир с клетками (пикселами), которые могут присутствовать (быть живыми) и отсутствовать (быть мертвыми). У каждой клетки есть окружение из восьми других, которые непосредственно прилегают к ней по горизонтали, вертикали и диагонали. Чтобы выжить, существующая живая клетка должна иметь два или три живых соседа — этого достаточно для поддержания жизни, но не слишком много. Если у любой живой клетки окажется менее двух соседних, она умрет из-за недостаточной населенности. Подобным образом любая живая клетка, у которой более трех живых соседей, умрет от перенаселения. Наконец, каждая живая клетка, у которой есть три живых соседа, активизируется и имитирует процесс размножения. Эти принципы обобщены в порождающих правилах на рис. 55. На рис. 56 показан пример такой модели и один жизненный цикл.

Благодаря этой простой математике и простому набору порождающих правил, которые применяются к клеткам на сетке, на игровом поле возникают странные и интересные модели, которые с течением времени меняются. Клетки живут и умирают по заданным правилам.

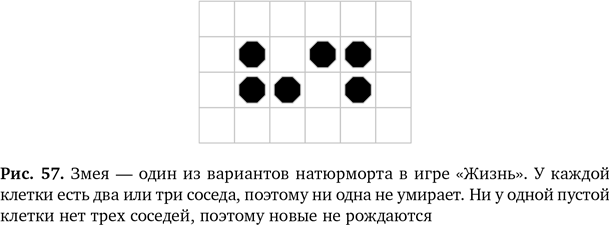
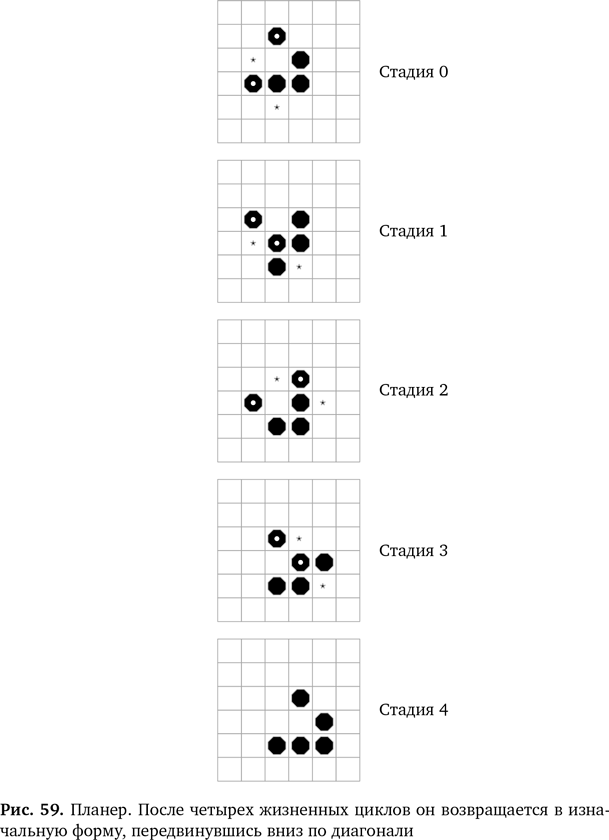
Сыграйте сами

Вы можете сыграть в эту игру самостоятельно. Для этого понадобится большая сетка. Для начала сгодится шахматная доска, но вы скоро осознаете, что нужно больше пространства. Больше подойдет доска для игры в го, если она у вас найдется. Как вариант, можно нарисовать большую сетку на самом большом листе бумаги, какой вы только найдете. В идеале лист должен быть бесконечным, но тогда он не поместится в вашу спальню… поэтому придется принять, что, если игра дойдет до края доски, нужно будет быстро найти еще место либо признать, что это конец «Жизни» и все ваши существа упадут с края «вселенной».

Необходимо как-то помечать рождающиеся клетки. Полезно также выделять те, которые в следующем раунде умрут. Убирать их нельзя — они нужны, чтобы просчитать все изменения. К примеру, можно взять камни для игры в го — замените черные на белые, чтобы показать, какие клетки скоро умрут (и отправятся на небо). Еще вам понадобится как-то помечать квадраты, в которых зародится жизнь. Для этого используйте более мелкие предметы (например, бусины) другого цвета. Можно использовать три вида монет или цветных бусин (но, если в вашем мире закипит жизнь, их понадобится очень много).

Теперь остается только произвольно разместить фишки на доске, а потом рабски следовать законам «Жизни». В вашем мире это эквиваленты физических законов. Сначала определите все рождения и смерти, заменив фишки на новые на всей доске, а потом уберите умирающие клетки и замените живые на новорожденные, чтобы подготовиться к следующему раунду. Чтобы играть в «Жизнь», нужно уделять много внимания деталям. Если вы сделаете ошибку с одной клеткой, у вас получится совершенно другой расклад.

В интернете вы найдете самые разные симуляции и с их помощью увидите, как развивается жизнь в более крупных масштабах. Конечно, если вы умеете программировать, то попробуйте создать собственный вариант. В систему Turtle («Черепаха»), разработанную в Оксфордском университете (www.turtle.ox.ac.uk), входит программа игры «Жизнь», которая может послужить образцом.

Паноптикум жизни

Конвей обнаружил, что некоторые комбинации являются статичными. Они остаются в одном и том же месте игрового поля без изменений, поэтому он назвал их натюрмортами — как, например, змею на рис. 57. Какие еще простые начальные комбинации, относящиеся к натюрмортам, вам удастся найти?

Некоторые шаблоны меняют форму, проходя через фиксированный набор вторичных шаблонов, в конце концов возвращаются к исходному варианту — и снова начинают бесконечный повторяющийся цикл. Их назвали осцилляторами. Например, очень простой осциллятор, так называемая мигалка, показан на рис. 58. Если начать с набора мигалок, которые находятся на достаточном расстоянии, чтобы не мешать друг другу, вы создадите замечательные мерцающие узоры. Такие комбинации из группы осцилляторов называются пульсарами — по имени необычных звезд, на которых с определенной периодичностью происходят всплески энергии.

Коллега Конвея Ричард Гай натолкнулся на удивительные фигуры, которые сохраняют форму, но передвигаются по сетке. Их назвали планерами (рис. 59). В целом движущиеся конфигурации называют космическими кораблями.

В игре «Жизнь» даже можно имитировать логические вентили. Как мы говорили выше, это базовые составляющие компьютера. Их делают из транзисторов, нейронов и… из клеток игры «Жизнь». Это значит, что, располагая достаточно большой сеткой, можно создать на ней работающий компьютер — исключительно из клеток, следующих этим простым правилам.

Моделируем новые миры

Информатики начали предлагать новые разновидности игры — трехмерные решетки, шестиугольную решетку и так далее. Изменив игровое пространство и правила, они обнаружили, что по мере того, как компьютер повторяет нужные действия и вносит изменения, на решетке появляются еще более интересные конфигурации.

Со временем изобретение Конвея стали называть клеточным автоматом и сочли новым способом проводить вычисления. Правила можно адаптировать так, чтобы клетки проводили вычисления разного рода. Простые клетки с простыми правилами можно заменить и даже усложнить. Каждая клетка в этом случае становится автоматом, который находится в определенной позиции на решетке и содержит код с собственным набором правил. Когда автомат входит в контакт с информацией, размещенной на решетке, он «переваривает» сначала свои данные, а затем данные из ближайших окрестностей, и на выходе дает результат. Результат зависит от нескольких предыдущих (скажем, 10) состояний клетки. Изначальными правилами Конвея при этом полностью пренебрегают.

Такого рода сложные клеточные автоматы находят самое разное применения. Их, например, настраивают на изучение природы — чтобы они исследовали, как в тропических лесах распространяются растения, как развиваются коралловые рифы, как проявляется сейсмическая активность, как мигрируют животные. Каждая клетка при этом становится абстракцией небольшого участка мира. В ней закодированы правила поведения и взаимодействия с другими клетками, свойственные интересующему ученых объекту. Клеточные автоматы обеспечили новый способ изучения экологии с помощью компьютерного моделирования на основе клеток.

Клеточный автомат помогает понять, как на дорогах образуются пробки и как в популяции распространяется болезнь. В криптографии данные, которые нужно зашифровать, размещают в сетке и исследуют с помощью автомата. Благодаря простым правилам каждый в состоянии зашифровать сообщение. Но расшифровать его, не зная ключа, нелегко. Клеточные автоматы даже использовали для сочинения музыки — и для многих других задач. Неплохой результат для того, что началось с несложной игры на простой доске.

Игры, в которые играют люди

Любите играть в слова?

В игре Конвея не было двух конкурирующих игроков, то есть отсутствовал соревновательный момент, который часто привлекает нас в играх. Вот простая игра под названием «Бусы, хлеб, хлеб», в которую мы сейчас попробуем сыграть (возможно, вас порадует, что в баню идти не придется). Сначала рассмотрим правила. Запишите слова:

БУСЫ, ХЛЕБ, БАНЯ, ПЛУГ, СНЕГ, ГАТЬ, УРОН, ОРЕХ, МАРС.

Вот правила:

1. Первый игрок выбирает слово из списка, вычеркивает его из списка и записывает.

2. Второй игрок делает то же самое с еще не вычеркнутым словом.

3. Игроки продолжают ходить до тех пор, пока кто-нибудь не выиграет. Победителем становится тот, кто первый сможет собрать три слова с одной и той же буквой.

Например, игра может пойти так:

 

игрок 1 берет БУСЫ,

игрок 2 берет ХЛЕБ,

игрок 1 берет БАНЯ,

игрок 2 берет ГАТЬ,

игрок 1 берет ПЛУГ,

игрок 2 берет ОРЕХ,

игрок 1 берет УРОН...

 

…и выигрывает, собрав БУСЫ, ПЛУГ и УРОН. Это три слова, в которых есть буква У.

 

Сыграйте несколько партий, чтобы понять принцип. А потом читайте дальше — и найдете хитрый способ выигрывать… а может, догадаетесь сами? Мы вернемся к этому чуть позже.

ПОДСКАЗКА. Подумайте, как расположить слова в квадрате, чтобы было легче заметить выигрышный набор слов. Вы уже знаете очень похожую игру!

Как обыграть человека

Мы знаем, что компьютеры творят чудеса, и одно из таких чудес — умение выигрывать у людей в игры. Компьютер может победить чемпиона мира по шахматам, но как? А может ли обычный листок бумаги действовать столь разумно, что будет играть так же хорошо, как человек? Да. Если правила будут верными. И сейчас у вас есть шанс сыграть против такого листка и посмотреть, что получится.

Крестики-нолики — популярная игра на основе сетки, позволяющая быстро развлечься и посоревноваться. Давайте сыграем — и заодно рассмотрим базовые принципы, благодаря которым компьютеры могут участвовать в играх. В игре «Крестики-нолики» участники по очереди делают ход на поле 3×3. Один ставит нолики, другой — крестики. Сделать ход — значит написать X или 0 в пустой клетке на доске. Первый, кто поставит три символа в одну линию по горизонтали, вертикали или диагонали, выигрывает. Если никому не удастся это сделать, получается ничья.

Игра со страницей, на которой напечатан рис. 60, будет нелегкой! Когда настанет ее очередь ходить, делайте, что сказано в инструкциях к рисунку. Потом делайте любой ход. Страница начинает первой и играет крестиками.

Ну что, выиграла страница? Или получилась ничья? Или вам все же удалось обыграть этот листок бумаги?

В лучшем случае (если вы не мухлевали) будет ничья. Удалось ли странице сыграть достойную партию? Она немного разбирается в крестиках-ноликах и действует осмысленно. Как и в игре «Жизнь», для выигрыша здесь тоже требуются тщательно продуманные и проверенные инструкции — знакомый нам теперь алгоритм. Обычно такие инструкции хранятся в памяти компьютера, чтобы он им следовал.

Но компьютеры делают только то, что придумал программист. Если что-то пойдет не так, его действия окажутся не слишком разумны. Мы написали правила, приведенные выше, в расчете на то, что страница будет ходить первой… а если она начнет второй? Попробуете? Так ли умно она играет? Мастерство программиста заключается в том, чтобы написать правила для любой вероятности. Хотите написать хорошие инструкции для игрока 2? Позаимствуйте знания у нашего листка бумаги, и вы будете непобедимы.

Но действительно ли это интеллект? Ведь тут просто выполняются кем-то написанные правила. Может быть, надо обращать внимание на результат. Лист бумаги и правда играет так же хорошо, как лучшие игроки-люди, и он непобедим — по крайней мере когда ходит первым. В более сложных играх, например в шахматах, алгоритмы должны быть более изощренными, но идея остается прежней. Для этого алгоритма человек разработал точную последовательность ходов. Однако шахматы слишком сложны, чтобы заранее определить все необходимые для победы правила. Поэтому компьютерам-шахматистам необходим алгоритм, указывающий, как прийти к победе самостоятельно.

Сегодня компьютеры обыгрывают в шахматы гроссмейстеров. Раньше мы считали, что шахматы — самый сложный тест для компьютерного интеллекта. Однако если у вас есть быстрая и достаточно изощренная программа плюс достаточный объем памяти, чтобы компьютер мог просчитать тысячи и тысячи возможных комбинаций для любой позиции на доске, то следует выбрать ту, которая открывает возможности для наилучших позиций — и таким образом позволяет обыграть человека. Это называется поиском по дереву. Мы использовали подобный алгоритм при разработке инструкции для безупречной партии в крестики-нолики. Однако в шахматах слишком много вариантов, чтобы подобным образом охватить все. Шахматные компьютеры смотрят на много ходов вперед, но не до конца игры. Хороший шахматист-человек не просто просчитывает абсолютно все ходы — он ищет знакомые комбинации и формирует определенную последовательность. Он играет путем сопоставления с образцом.

Существуют и более сложные настольные игры, которые ставят перед компьютерами новые задачи, — например, древняя игра го. В отличие от шахмат, го — популярная стратегическая игра для двоих, у которой простые правила и в которую играют на поле-сетке 19 на 19. Однако число возможных сочетаний на доске огромно, и, чтобы провести такой анализ, о котором мы говорили выше, нужно просчитать число ситуаций, превышающее число атомов во вселенной. Компьютеры не могут выиграть в го, как выигрывают в шахматы.

Поэтому исследователи подошли к го иначе, чем к шахматам, для которых компьютер запрограммировали именно на хорошую игру. Чтобы победить мастера го, компьютерную программу AlphaGo снабдили мощным обучающим алгоритмом общего назначения, в котором использовали уже рассмотренные нами методы. Алгоритм AlphaGo извлекал победные комбинации из сыгранных партий и совершенствовал навыки с каждым выигрышем или поражением. В итоге в 2015 г., многому научившись, AlphaGo выиграла у профессионального игрока в го в турнире из нескольких партий. В 2016 г. она победила одного из лучших мастеров мира Ли Седоля в турнире из пяти партий со счетом 4: 1. Это еще один успех на счету искусственного интеллекта, который играет в игры.

Компьютер играет и в другие типы игр без доски, например в покер. Предназначенные для этой игры покерные боты могут выиграть у человека, но им приходится иметь дело с иным типом игровой сложности. В отличие от шахмат и го, где все на виду, покер — игра с неполной информацией. Вам неизвестно, какие карты есть у других игроков и какие карты сдадут. Покерные боты часто обращаются к вероятности, чтобы сделать наиболее верную догадку, — почти как искусные игроки. Исследования в этой области помогают ученым понять, как мы, люди, справляемся с риском и принимаем решения.

Совершенствуем игру

Четко описанные наборы правил для ИИ вроде нашего алгоритма для крестиков-ноликов постоянно возникают в настоящих играх. Часто они стоят за компьютерными версиями настольных игр, в которые играют против компьютера. В многопользовательских играх бывают так называемые «несобственные персонажи» (за которыми не стоят игроки). В них интегрированы правила для искусственного интеллекта, контролирующие их взаимодействие с настоящими игроками, что делает игровой процесс интересным и достоверным. Также ИИ часто следит за показателями игроков-людей, чтобы игра была достаточно сложной и интересной. В зависимости от этого, например, выбирается уровень сложности. Иногда искусственный интеллект скрыт и решает другие задачи — например, выясняет, на какой телефон и экран какого размера загружается приложение, или проверяет, достаточно ли хорошо работает сетевое соединение. Еще он фиксирует, насколько хорошо справляются игроки, какие роли они выбирают чаще всего и реже всего, по каким причинам они прекращают игру и что оказывается слишком трудным для большинства игроков. Все эти данные позволяют разработчикам адаптировать игровой процесс к потребностям и повысить объем покупок в игре.