
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы упрощения задач в прикладной газовой динамике
Математическое описание движения жидкой среды общими дифференциальными уравнениями, учитывающими все физические свойства, присущие этой среде, является сложной, а в большинстве случаев и неразрешимой задачей. Для прикладной газовой динамики характерным является использование упрощенных моделей жидкости и их движений, позволяющих получить результаты, удовлетворяющие по точности практику. К числу «методов упрощения» задач газовой динамики можно отнеси следующие: 1) Формулировка задачи в рамках установившегося движения. Несмотря на то, что в природе и технике практически всякое течение жидкости является, строго говоря, неустановившимся (нестационарным), во многих случаях отклонение скорости от некоторого среднего значения по времени бывает достаточно малым по сравнению с величиной скорости, и это дает основание приближенно считать движение установившимся («квазистационарным»). 2) Переход от пространственного к двумерному или одномерному течению. Одномерные задачи при установившемся течении жидкости составляют предмет рассмотрения отдельного раздела газовой динамики – газовой динамики элементарной струйки, который иногда ещё называют газовой гидравликой. 3) Выбор наиболее простой модели жидкости – идеальной жидкости. Моделью идеальной жидкости пользуются в расчетах, выполняемых в первом приближении, когда явлениями трения пренебрегают, а также при расчетах тех областей течения, которые расположены на значительном расстоянии от обтекаемой поверхности (стенок канала), т.е. там, где влияние трения незначительно. 4) Переход от сжимаемой к несжимаемой жидкости. Существуют методы, позволяющие пересчитывать данные, полученные для течения несжимаемой жидкости, на случай движения сжимаемой жидкости. При таком подходе расчет течения несжимаемой жидкости является первым этапом решения задачи, а учет сжимаемости – вторым. 5) Использование модели баротропной жидкости, у которой плотность является функцией только давления, в отличие от бароклинной жидкости, плотность которой зависит и от давления и от температуры. Если при расчете течения жидкости известен термодинамический процесс, т.е. давление и плотность связаны однозначной зависимостью, например уравнением политропного процесса p/ρn=Const, то жидкость в этом случае подходит под понятие баротропной жидкости.
Скорость звука Скорость звука – скорость распространения в упругой среде малых возмущений. Малыми или слабыми принято называть такие возмущения среды, в которых местное изменение давления среды в точке возмущения, т.е. амплитуда давления, пренебрежимо мало по сравнению с общим давлением. Понятие скорости звука является одним из важнейших в теории течения сжимаемой жидкости.
Таким образом, в жидкости распространяется слабая волна сжатия, фронт которой можно представить в виде перемещающегося вдоль трубы (точнее - вдоль жидкости) сечения А-А, отделяющего сжатую – «возмущённую», область жидкости с параметрами p + dp, r + d r, T + dT (слева от сечения А-А)от невозмущённой области жидкости, т.е. области, куда возмущения ещё не проникли (справа от сечения А-А). Если перемещение сечения А-А за время dt обозначить dx, то скорость распространения фронта слабой волны в этом случае может быть выражена как dx / dt. Скорость движения фронта слабой волны относительно жидкости называют скоростью звука и обозначают обычно а. «Относительность» особенно важно иметь в виду, поскольку жидкость в общем случае в момент возникновения в ней возмущения не обязательно должна находиться в состоянии покоя, а может изначально двигаться с некоторой скоростью.
За время dt фронт волны – сечение А-А, переместится на расстояние dx = a × dt и при этом будет сжат «новый слой» жидкости, т.е. произойдет уплотнение жидкости - увеличение плотности распределения массы в элементарном объёме dV = F × dx = F × a × dt, заключённом между начальным и конечным в указанный промежуток времени положениями сечения А-А. Поскольку в рассматриваемом элементарном объёме dV нет источников и стоков, то приращение массы жидкости в этом объёме может происходить только за счет притока в него за время dt некоторого количества жидкости из «возмущённой» области со скоростью W. Очевидно, что из уравнения неразрывности для рассматриваемого случая: dV × d r = (r + d r) × F × W × dt или F × a × dt × d r = (r + d r) × F × W × dt, где F – площадь поперечного сечения трубы, dV × d r - изменение массы жидкости в элементарном объёме dV; (r + d r) × F × W × dt – масса жидкости, притекающая в элементарный объём dV за время dt; с точностью до малых величин первого порядка (пренебрегая бесконечно малой величиной второго порядка F × W × d r × dt) можно получить следующее соотношение: a × d r = r W. (1) Применим к рассматриваемому элементарному объёму dV закон о сохранении количества движения, не учитывая при этом действия сил трения в жидкости (допустим, что жидкость идеальная). Изменение количества движения элементарного объёма d (mW) (здесь m – масса элементарного объёма) должно быть равно импульсу внешних сил, приложенных к этому объёму. В рассматриваемом случае в качестве внешних сил выступает только поверхностная сила, обусловленная разностью (градиентом) давления в звуковой волне dp. Заменяя массу произведением плотности на объём, и учитывая, что скорость движения рассматриваемого объёма в начальный момент времени (до прохождения через него фронта волны) была равна нулю, получим уравнение движения (уравнение количества движения) для рассматриваемого элементарного объёма: (r + d r) × F × a × W × dt = F × dp × dt, где слева стоит приращение количества движения элемента, а справа – импульс сил, действующих на элемент за время dt. Из уравнения движения, рассуждая аналогично предыдущему (пренебрегая бесконечно малой величиной второго порядка F × a × W × d r × dt), получим ещё одно соотношение a r W = dp. (2) Исключив из полученных соотношений (1) и (2) скорость W, получим уравнение для определения скорости звука:
Для того чтобы воспользоваться уравнением (3) нужно знать, как происходит процесс распространения звуковых волн, т.е. для каких условий следует вычислять производную dp / d r. Одним из первых, кто практически решил эту задачу, был Исаак Ньютон. Он вычислил скорость звука в воздухе при атмосферном давлении и комнатной температуре (при этих параметрах воздух с хорошим приближением можно рассматривать как совершенный газ, для которого справедливо уравнение состояния p = r RT). Ньютон считал, что процесс распространения звука в воздухе происходит в изотермических условиях и производную надо брать при постоянной температуре, т.е. при условии T = const. Воспользовавшись уравнением Бойля-Мариотта для изотермического процесса в совершенном газе pv = const или p = r × const, для производной получим
а для скорости звука
Однако при прямых измерениях скорости звука в воздухе было получено значение а примерно на 20% превосходящее величину, вычисленную Ньютоном. Причина этих расхождений была установлена Лапласом, который отметил, что поскольку звуковые колебания (волны) в упругой среде (воздухе) распространяются очень быстро, то можно предположить, что сколь-нибудь заметного теплообмена между зонами разряжения и сжатия звуковой волны и окружающей средой при этом не успевает произойти (что, кстати, хорошо подтверждается опытом). Поэтому, процесс распространения звуковой волны можно считать адиабатным и изоэнтропийным и производную в (3) нужно брать при постоянной энтропии, т.е. при условии S = const. Уравнение Лапласа для скорости звука
В случае изоэнтропийного процесса плотность и давление будут связаны уравнением изоэнтропы p / r k = const. Тогда dp = k × r k - 1 × d r × const и dp / d r = k × r k - 1 × const, определяя постоянную из уравнения изоэнтропы, для производной (¶ p / ¶ r) S получим
а для скорости звука
Для совершенного газа, имея в виду, что p / r = RT, может быть установлена однозначная связь скорости звука с абсолютной температурой газа
Из соотношения (8) видно что, чем выше температура газа, тем больше скорость распространения звуковых волн в нём. Кроме того, скорость звука зависит от физических свойств газа (k и R). Этот вывод находится в полном соответствии с газокинетическими представлениями о процессе распространения малых возмущений в среде, состоящей из движущихся молекул. Скорость распространения возмущений должна зависеть от скорости движения молекул, которая, в свою очередь, определяется температурой. Известно, что скорость движения молекул газа (средняя скорость) близка к скорости звука. В этой связи необходимо подчеркнуть, что квадрат числа Маха M 2 = W 2 / a 2 определяет соотношение в потоке средней кинетической энергии направленного движения газа как целого и средней кинетической энергии беспорядочного движения молекул, т.е. частиц, составляющих это целое.
Следует иметь в виду, что формула (7), как и уравнение Лапласа (5) справедливы и для газов и для капельных жидкостей и для твердых упругих тел, в то время как формула (8) имеет отношение только к совершенному газу. В несжимаемых средах r = const, d r = 0 и a = ¥, т.е. звуковые волны распространяются мгновенно.
|
||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.56.45 (0.013 с.) |
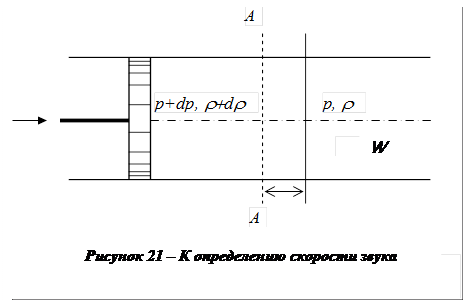 Рассмотрим процесс распространения малого (слабого) возмущения в сжимаемой среде. Пусть неподвижная сжимаемая жидкость с заданными параметрами r, p, T находится в длинной трубе постоянного по длине сечения, ограниченной слева поршнем (см. рис.21). В некоторый момент времени поршень начинает двигаться слева направо с постоянной скоростью W и «наталкивается» на неподвижную жидкость. «Слой» жидкости, непосредственно примыкающий к поршню, в результате движения поршня несколько уплотняется (сжимается) и давление в нем повышается – до величины p + dp; кроме того, жидкость в этом «слое» из состояния покоя приходит в движение со скоростью W. Далее сжимается и приходит в движение «слой» жидкости, примыкающий к «первому слою», и т.д. Можно представить себе движущуюся в жидкости «слабую волну сжатия», подобную той, которая возникает при трогании с места длинного железнодорожного состава – вагоны не одновременно, а последовательно (поочерёдно) приходят в движение благодаря упругости сцепки. Другим примером может служить картина падающих костяшек домино, выстроенных в длинный ряд.
Рассмотрим процесс распространения малого (слабого) возмущения в сжимаемой среде. Пусть неподвижная сжимаемая жидкость с заданными параметрами r, p, T находится в длинной трубе постоянного по длине сечения, ограниченной слева поршнем (см. рис.21). В некоторый момент времени поршень начинает двигаться слева направо с постоянной скоростью W и «наталкивается» на неподвижную жидкость. «Слой» жидкости, непосредственно примыкающий к поршню, в результате движения поршня несколько уплотняется (сжимается) и давление в нем повышается – до величины p + dp; кроме того, жидкость в этом «слое» из состояния покоя приходит в движение со скоростью W. Далее сжимается и приходит в движение «слой» жидкости, примыкающий к «первому слою», и т.д. Можно представить себе движущуюся в жидкости «слабую волну сжатия», подобную той, которая возникает при трогании с места длинного железнодорожного состава – вагоны не одновременно, а последовательно (поочерёдно) приходят в движение благодаря упругости сцепки. Другим примером может служить картина падающих костяшек домино, выстроенных в длинный ряд.
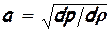 . (3)
. (3)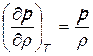 ,
,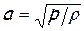 . (4)
. (4)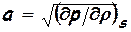 . (5)
. (5)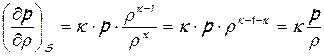 , (6)
, (6)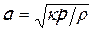 . (7)
. (7)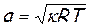 . (8)
. (8)


