
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Каким образом алгоритм завершает работу?Содержание книги
Поиск на нашем сайте
С помощью диаграммы
Композиция машин Тьюринга
Для организации такой работы достаточно построить объединенную таблицу машины Тьюринга, приписав к первой таблице вторую (справа) и заполнив пустые клетки первой таблицы командой перехода к начальному состоянию второй программы. f(x)=(x+1)*2
Итерация (повторение) машин Тьюринга В этом случае повторяем выполнение одной и той же команды конечное число раз. По окончании первого выполнения на ленте остается промежуточный результат необходимый для второго выполнения и т.д. Для обеспечения второго и последующих выполнений необходимо в некоторые пустые клетки таблицы вписать команду перехода на начало. Во все пустые клетки эту команду вписывать нельзя, так как измененная таким образом программа не сможет заканчиваться. f(X)=X+L eeeeX*Leeeee
3) Алгорифмы Маркова (нормальные алгорифмы) используются для представления алгоритмов, преобразующих одну цепочку символов (исходные данные) в другую (результат).
Отличие алгорифмов Маркова в том, что каждый шаг преобразования позволяет выполнить замену не одного символа, а целого слова в исходной цепочке. Если применив алгоритм Замены выполняются в соответствии с заданным правилом, которые и будут определять алгоритм. Такой алгоритм называется вербальным.
Расширим алфавит Если такое правило срабатывает, то в исходной строке отыскивается подстрока Для определения алгоритма нужно задать не одно правило, не одну формулу подстановки, а множество, причем необходимо определить порядок их применения. Для этого вводится еще одно понятие схемы алгоритма. Схемой – называется слово в расширенном алфавите, имеющее вид Если в строке, которая преобразуется алгорифмом встречается левая часть какой-то формулы Если какая-то подстановка действует на исходную строку, причем левая часть встречается в строчке многократно, то формула подстановки применяется один раз. Причем применяется к самому левому вхождению. При заменах могут использоваться пустые строки
Если в схеме используется несколько правил, в которых правые части совпадают, а левые части являются подстроками, которые можно объединить в какое-то множество, то пишут
Пустая строка может встречаться и в левой части. Если есть такие правила, то пустота замениться слева. В этом случае при составлении схемы, нужно думать о том, чтобы алгоритм был применим. Суперпозиция Будем предполагать, что все функции к которым применяется операция суперпозиции определены на одном и том же наборе входных данных. Обозначим функции, к которым применяется операция суперпозиции:
Если какой-то элемент из набора
Входными данными для
Все рассматриваемые функции являются частными, т.е не всюду определенными; могут существовать такие комбинации аргументов, для которых значение функции не существует. Функция 1. Значение 2. Примитивная рекурсия Операция примитивной рекурсии имеет два операнда
Первый операнд, функция
Множество всех функций которые можно получить из базового набора Операция минимизации Операция минимизации Оператор минимизации может превратить всюду определенную функцию в частичную. Множество функций, получаемых применением к базовому набору Примеры определения функций при помощи этих трех операций: 1)
3)
5) В математической логике и теории алгоритмов под разрешимостью подразумевают свойство формальной теории обладать алгоритмом, определяющим по данной формуле, выводима она из множества аксиом данной теории или нет. Теория называется разрешимой, если такой алгоритм существует, и неразрешимой, в противном случае. Вопрос о выводимости в формальной теории является частным, но вместе с тем, важнейшим случаем более общей проблемы разрешимости.
Факт алгорифмической неразрешимости доказал в 1970 году российский математик Ю.В. Матиясевич.
Задачи, для которых не существует алгоритма, решающего ее, называют алгорифмически неразрешимыми. но аглорифмическая неразрешимость некоторой общей задачи не означает, что не могут быть созданы алгоритмы, решающие частные случаи задачи.
В теории вычислимости алгоритмически неразрешимой задачей называется задача, имеющая ответ да или нет для каждого объекта из некоторого множества входных данных, для которой (принципиально) не существует алгоритма, который бы, получив любой возможный в качестве входных данных объект, останавливался и давал правильный ответ после конечного числа шагов.
Проблема умирающей матрицы: для данного конечного множества квадратных матриц n × n определить, существует ли произведение всех или некоторых из этих матриц (возможно, с повторениями) в каком-либо порядке, дающее нулевую матрицу. Проблема неразрешима даже для n=3 (разрешимость для n=2 является открытым вопросом[2])
6) Ключевым подходом в алгоритмизации является сведение задачи к подзадачам, а способ такого сведения определяет метод разработки алгоритмов.
1. Суперпозиция – самый простой метод. Состоит в том, что решение сложной задачи представляется как последовательное решение более простых задач, при этом результат решения предыдущей задачи используется в качестве входных данных для решения следующей задачи. Разбивать задачу на подзадачи, можно: 1) разбивать исходные и выходные данные на части и упрощать их; под разбиением понимаем разделение структуры данных на части, например, разделение вектора из десяти компонент на два по пять компонент или разделение текста на предложения; под упрощением понимаем такие ситуации, когда, например X – число и его нельзя разбить на части, но его можно разложить в сумму X= X1+ X2, так, что результаты f(X1) и f(X2), отыскиваются проще, чем f(X). 2) производить декомпозицию функции f, т.е превращать ее в суперпозицию более простых, f(X)= g(h(s(X))) или f(X)= g(X, h(X), s(X)) На практике используется совмещение этих методов. 2. Итерация – частный случай предыдущего метода. f(X)=g(g(g(g(X))) или f(X)=g(X,s(X),s(X),s(X)) Однородность подзадач позволяет значительно сократить длину текста алгоритма за счет применения операторов повторения (циклов). 3. Метод последовательного приближения Частный случай итерации. Сначала каким-либо образом угадывается значение 4. Метод обратной функции Иногда обратная задача решается значительно более просто, чем исходная. Тогда имеющийся алгоритм решения обратной задачи, можно использовать для решения прямой задачи.
5. Рекурсия При использовании рекурсии решение задачи сводится к решению той же самой задачи, но на более простом входном наборе данных. При этом появляется необходимость в дополнительных вычислениях, связанных со сведением одного набора данных к другому. При вычислении рекурсивной функции всегда выделяется рекурсивная и не рекурсивная части.
6. Метод полного перебора Метод полного перебора применим в тех случаях, когда решение принадлежит некоторой конечной области и может быть найдена простая функция для проверки выбранного решения. Сложность заключается в том, что при увеличении количества исходных данных быстро увеличивается необходимое число проверок.
7)
Качество (программных средств) можно определить как совокупную характеристику исследуемого ПО с учётом следующих составляющих: · Надёжность · Сопровождаемость - процесс улучшения, оптимизации и устранения дефектов программного обеспечения (ПО) после передачи в эксплуатацию · Практичность · Эффективность · Мобильность · Функциональность
8) Алгоритм 1. хотя бы один шаг этого алгоритма представляет собой обращение 2. хотя бы один шаг этого алгоритма представляет собой обращение
Реализация рекурсии
1) Описание функции в общем случае "пассивно". Для начала вычислений в программе должно быть обращение к процедуре или функции, в котором обязательно указываются условия решения этой задачи с помощью вызываемой функции. Условия определяются значением фактических параметров при вызове процедуры или функции. При реализации процедур или функций код этих процедур (функций) размещается в оперативной памяти, т.е к моменту обращения к нему, он загружен в память. При компиляции процедуры необходимо решить один важный вопрос: как быть с ее локальными переменными и параметрами, передаваемыми по значению? Есть два варианта: 1. Локальные данные, используемые в подпрограмме, размещаются в памяти статически, это означает, что и объем памяти, необходимый для их размещения, и адреса всех констант и переменных определяются еще на этапе трансляции. Преимущество такого способа в том, что не тратится время на выделение памяти. Однако, при таком распределении памяти, возникают проблемы с реализацией рекурсии, т.к при каждом вызове мы должны хранить свои копии локальных данных.
2. Динамическое распределение памяти, при таком распределении, память для локальных данных выделяется при вызове процедуры или функции. Такая процедура называется реинтерабельной. Код такой процедуры называют чистым кодом.
Модель стека Стек представляет собой область памяти со смежными адресами. Размер стека фиксирован. Его размер определяется до начала выполнения программы. Базовый адрес – начало стека.
Для стека выполняются две операции: 1. Поместить данные в вершину стека (втолкнуть, push) 2. Вытолкнуть, pop
Стек в программировании используется для нескольких целей: 1. как вспомогательная рабочая память для организации вычислений 2. реализация вызовов процедур и функций
При вызовах процедур и функций в стек помещается информация о параметрах, которые передаются в процедуру или функцию. Для передачи параметров в стеке выделяется целый блок. При вызове функции через стек возвращается еще и результат.
Кроме того, если в процедуре или функции описаны локальные данные, они также помещаются в стеке. Для того чтобы реализовать возврат в нужную точку соответствующую именно этому вызову, нужно запоминать адрес возврата. Адрес точки возврата запоминается в стеке автоматически при выполнении команды передающей управление с возвратом. При возврате, из вершины стека выталкивается (удаляется) вся информация, которая была размещена при работе процедуры или функции.
Begin for i:= 1 to n do {Цикл 1} for j:= 1 to n do {Цикл 2 и начало тела цикла 1} begin c [ i, j ]:= 0; {Начало тела цикла 2} for k:= 1 to n do {Цикл 3} c[i, j]:= c[i, j] + a[i, k] * b[k, j]; {Тело цикла 3} end {Конец тела цикла 2; конец тела цикла 1} end; Тип данных matrix определен вне процедуры как двумерный массив. Время доступа к элементам не учитываются при анализе алгоритмов. Прежде всего, выберем параметр V. Простой анализ текста показывает, что за параметр сложности данных можно взять размер n матриц, участвующих в вычислениях. Поскольку процедура представляет собой цикл по переменной i, то ее временная сложность Т α (n) = n· T (1). В свою очередь, T (1) = n· T ( 2 ) и, следовательно, Т α (n) = n·(n· T ( 2 )). Тело цикла 2 состоит из одного оператора присваивания и цикла 3. Таким образом, Т α (n) = n·(n·(1 + n· T ( 3 ))). Тело цикла 3 включает умножение, сложение и присваивание (3 операции). Окончательно получаем Т α (n) = n ·(n ·(1 + n ·3)) = 3 n 3 + n 2 End;
· Для вычисления сложности рекурсивных алгоритмов используется рекуррентное уравнение: T a (X)=T a (f(X))+ Tf(X)+ Th(X)+ Tс (X,S) T a (S)=Tc(S,S)+ Ts(S) Здесь T a(X) – общая сложность рекурсивного алгоритма T a(f(X)) – сложность предыдущего уровня рекурсии Tf(X) – сложность вычисления аргументов при рекурсивном вызове процедуры Th(X) – сложность нерекурсивных вычислений Tс(X, S) – сложность операции сравнения Ts(S) – сложность вычисления нерекурсивного начального значения Tc(S, S) – сложность операции сравнения для нерекурсивного начального значения Пример: Function F(n); begin If (n=0) or (n=1) {проверка возможности прямого вычисления} Then F:= 1 Else F:=n*F(n-1); {рекурсивный вызов функции} End; X = x, S = 1, x = 1 f(X)=X-1, FACTORIAL (x-1) Tf(X)=1, FACTORIAL (x-1) Th(X) = 2, FACTORIAL:= x * FACTORIAL (x-1) Tc(X,S)=l, x = 1 Ts(S) = 1. FACTORIAL:= 1 Таким образом, система уравнений превращается в Тa(x) = Тa(х-1)+4, Тa(1) = 2. Ее решение – Тa(x) = 4х-2.
В случае косвенной рекурсии рекуррентное уравнение имеет вид:
12) Поиск алгоритма min сложности – оптимизация алгоритма.
Одна из задач, которая обычно ставится при разработке алгоритмов и программ - минимизация требуемых программой ресурсов. Особенно это касается системного программного обеспечения: программ операционной системы, трансляторов, систем управления базами данных и знаний и т. д., т.е. программ, имеющих большое количество пользователей и испытывающих как товар, большую конкуренцию на рынке программных средств.
Существует несколько самостоятельных аспектов оптимизации программ, из которых выделим два: · оптимизация, связанная с выбором метода построения алгоритма; · оптимизация, связанная с выбором методов представления данных в программе.
Первый вид оптимизации имеет глобальный характер и (при удачной оптимизации) ведет к уменьшению порядка функции сложности - например, замена алгоритма с Т a (V) = O(FS) на алгоритм с T a (V) = O(V4). Он зависит от того, как задача разбивается на подзадачи, насколько это разбиение свойственно самой задаче или является только искусственным приемом.
Второй вид оптимизации, не меняя структуры программы в целом, ведет к экономии памяти и/или упрощению работы со структурами данных, повышению эффективности вспомогательных процедур, обеспечивающих "интерфейс" между прикладным уровнем (на котором мыслим в терминах высокоуровневых объектов - графов, матриц, текстов и т. д.) и машинным уровнем, поддерживающим простейшие типы данных (числа, символы, указатели). Результатом этого обычно является уменьшение коэффициентов при некоторых слагаемых в функции сложности (при удачной оптимизации - при наиболее значимом слагаемом), но порядок функции сложности остается тем же.
Пример: вычисления числа Фибоначчи через формулу:
13) Задачи:
сложность задачи – сложность самого простого алгоритма. Поиск алгоритма min сложности – оптимизация алгоритма. Детерминированные вычисления – обычный, классический способ. Недетерминированные вычисления – существует в нескольких параллельно работающих экземплярах. Недетерминированный вычислитель исполняет недетерминированные алгоритмы. Разрешаем шаги с неоднозначным результатом – шаги, вырабатывающие сразу несколько значений для одной переменной. Эти значения могут использоваться:
Классы сложности задач:
Задача Q сводится к задаче Р за полином.время, если сущ-ет детерминированный полиномиальный алгоритм, преобразовывающий произвольный частный случай задачи Р так, что ответом для данного случая задачи Q является «да» тогда и только тогда,када ответом на соответсвующий случай задачи Р также является «да». вход для Q Вход для Р ответ Р Ответ Q
Полиномиальная сводимость – детерминированный полиномиальный алгоритм сводит одну задачу к другой NPC – подкласс NP, любая задача NP сводится к ним
14) Сортировка – процесс перегруппировки заданного множества объектов в некотором определенном порядке. Цель сортировки – облегчить последующий поиск элементов в таком упорядоченном (отсортированном) множестве. Сортировку массивов называют внутренней сортировкой, т.к. поскольку массивы хранятся в быстрой, оперативной, внутренней памяти ЭВМ, допускающей случайный (прямой) доступ к элементам. При анализе сложности алгоритмов сортировки будем учитывать только операции сравнения и пересылки записей.
Сортировка обменами: Производится последовательное упорядочение смежных пар элементов массива: x [1] и x [2], x [2] и x [3], … x [ N -1] и x [ N ]. Если первый элемент больше второго, то элементы переставляются. В итоге, после N –1 сравнения максимальное значение переместится на место элемента X [ N ], т.е. "вверху" оказывается самый "легкий" элемент – отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента (X [ N –1]), таким образом второй по величине элемент поднимается на правильную позицию и т.д. Таким образом, нужно выполнить данную процедуру N –1 раз. При первом прохождении нужно сравнить N –1 пар элементов, при втором – N –2 пары, при k -м прохождении – N ‑ k пар.
Program Sort1; Const N=10; Type mas=array[1..N] of real; Var x:mas; i,k:integer; a:real; Begin For i:=1 to N do {Ввод элементов массива} read(x[i]); For i:=1 to N-1 do {Сортировка} For j:=1 to N-i do If x[j]>x[j+1] then Begin a:=x[j]; x[j]:=x[j+1]; x[j+1]:=a; End; For i:=1 to N do {Вывод элементов массива} Write(x[i],’ ‘) End. Среднее число сравнений и обменов имеют квадратичный порядок роста: О (n 2), отсюда можно заключить, что алгоритм пузырька очень медленен и малоэффективен.
Begin for i:=1 to N do { Ввод элементов массива } read(a[i]); for i:=n downto 2 dobegin k:=i; {Запоминаем номер и } m:=a[i]; {значение текущего элемента} for j:=1 to i-1 do {Поиск максимального элемента} if a[j]>m thenbegin k:=j; m:=a[k] end; if k<>i thenbegin { Меняем местами с последним } a[k]:=a[i]; a[i]:=m end end; for i:=1 to N do { Вывод элементов массива } write(a[i]:3) end.
Бинарный поиск – Если у нас есть массив, содержащий упорядоченную последовательность данных, то очень эффективен двоичный поиск. Переменные Lb и Ub содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Мы начинаем всегда с исследования среднего элемента отрезка. Если искомое значение меньше среднего элемента, мы переходим к поиску в верхней половине отрезка, где все элементы меньше только что проверенного. Другими словами, значением Ub становится (M – 1) и на следующей итерации мы работаем с половиной массива. Таким образом, в результате каждой проверки мы вдвое сужаем область поиска. Так, в нашем примере, после первой итерации область поиска – всего лишь три элемента, после второй остается всего лишь один элемент. Таким образом, если длина массива равна 6, нам достаточно трех итераций, чтобы найти нужное число. Случайный поиск Случайным образом задается индекс в массиве, сравнивается элемент массива имеющий этот индекс с исходным, если равен, то возвращается индекс, если нет то операция повторяется.
Метод крайне не эффективен.
18)
Внешняя сортировка - это сортировка последовательных файлов, располагающихся во внешней памяти, размер которых слишком велик, чтобы можно было целиком переместить их в основную память и применить один из методов внутренней сортировки. Наиболее часто внешняя сортировка применяется в системах управления базами данных при выполнении запросов, и от эффективности применяемых методов существенно зависит производительность СУБД.
Очевидно, что любой алгоритм сортировки файла требует изъятия каких-то элементов из файла и включения их в файл на новые места. Таким образом, часть файла должна быть переписана на новое место (в новый файл или несколько новых файлов), а затем эти новые файлы должны быть объединены (слиты). Основным понятием будем считать понятие отрезка файла. Отрезком длины k является последовательность записей A i, A i+1,…A i+k-1 такая, что в ней все записи упорядочены по заданному ключу key.
Естественное слияние При использовании метода прямого слияния не принимается во внимание то, что исходный файл может быть частично отсортированным.
Первая серия упорядоченных записей и переписывается в файл B, вторая - в файл C и т.д. При слиянии первая серия записей файла B сливается с первой серией файла C, вторая серия B со второй серией C и т.д. Если просмотр одного файла заканчивается раньше, чем просмотр другого (по причине разного числа серий), то остаток файла целиком копируется в конец файла A. Процесс завершается, когда в файле A остается только одна серия
Многофазная сортировка При использовании рассмотренного выше метода сбалансированной многопутевой внешней сортировки на каждом шаге примерно половина вспомогательных файлов используется для ввода данных и примерно столько же для вывода сливаемых серий. Идея многофазной сортировки состоит в том, что из имеющихся m вспомогательных файлов (m-1) файл служит для ввода сливаемых последовательностей, а один - для вывода образуемых серий. Как только один из файлов ввода становится пустым, его начинают использовать для вывода серий, получаемых при слиянии серий нового набора (m-1) файлов. Таким образом, имеется первый шаг, при котором серии исходного файла распределяются по m-1 вспомогательному файлу, а затем выполняется многопутевое слияние серий из (m-1) файла с записью в файл m, пока один из них не станет пустым..
Метод трехфазной внешней сортировки дает желаемый результат и работает максимально эффективно (на каждом этапе сливается максимальное число серий), если начальное распределение серий между вспомогательными файлами описывается суммами соседних числел Фибоначчи.
19)
Для сокращения времени доступа к данным в таблицах используется так называемое случайное упорядочивание или хеширование.
Хеш-таблица – это обычный массив с необычной адресацией, задаваемой хеш- функцией. Хеширование (глагол «hash» в английском языке означает «рубить, крошить») применяется, когда реальное количество записей значительно меньше, чем количество возможных ключей.
Если входной поток информации абсолютно случаен, то в качестве хеш-функции можно использовать, например, функцию: h (a)= code (a) mod N При заполнении таблицы возникают ситуации, когда для двух неодинаковых ключей функция вычисляет один и тот же адрес: ki ≠ kj; h(ki) = h(kj). Данный случай носит название коллизия, а такие ключи называются ключи-синонимы.
Разрешение коллизий достигается путём рехеширования – специального алгоритма, который используется при размещении новой записи или при поиске существующей.
h(a)=(B code(a) +C) mod N, где B и C – константы При большом количестве элементов с одинаковым значением адреса будет получены кластеры (блоки) - последовательности подряд идущих записей, соответствующих одному и тому же адресу. Методы разрешения коллизий: Освобождение памяти
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.190.0 (0.019 с.) |

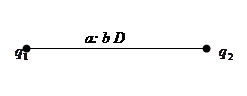 Диаграмма представляет собой геометрический объект (ориентированный граф), состоящий из вершин и дуг. Каждой вершине приписывается состояние машины Тьюринга: таким образом, вершин в диаграмме ровно столько, сколько имеется состояний. Дуге, соединяющей две вершины qi и qj, приписывается некоторый символ a алфавита A и двойка b D так, что запись a qi b qj D образует команду программы машины Тьюринга.
Диаграмма представляет собой геометрический объект (ориентированный граф), состоящий из вершин и дуг. Каждой вершине приписывается состояние машины Тьюринга: таким образом, вершин в диаграмме ровно столько, сколько имеется состояний. Дуге, соединяющей две вершины qi и qj, приписывается некоторый символ a алфавита A и двойка b D так, что запись a qi b qj D образует команду программы машины Тьюринга. Формализация понятия алгоритма: нормальные алгорифмы Маркова, определение и выполнение. Примеры.
Формализация понятия алгоритма: нормальные алгорифмы Маркова, определение и выполнение. Примеры.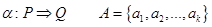
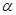 к строке
к строке 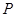 , мы, за конечное число шагов, получили результат
, мы, за конечное число шагов, получили результат 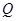 , то такой алгоритм будем называть применимым и обозначать
, то такой алгоритм будем называть применимым и обозначать 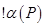
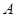 тремя символами «
тремя символами «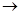 », «
», «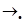 ». «|». Предполагается, что в алфавит
». «|». Предполагается, что в алфавит 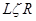 , где
, где 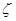 - один из двух символов: стрелка или стрелка с точкой,
- один из двух символов: стрелка или стрелка с точкой, 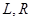 - любая цепочка символов в алфавите
- любая цепочка символов в алфавите 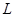 и она целиком заменяется на
и она целиком заменяется на 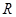 .
.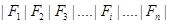 , где
, где 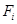 - формулы подстановок. Чем меньше номер, тем выше приоритет. Это значит, что если в цепочке символов, которая преобразуется с помощью алгоритма, встречается несколько подстрок, то применяться будет формула, имеющая минимальный номер.
- формулы подстановок. Чем меньше номер, тем выше приоритет. Это значит, что если в цепочке символов, которая преобразуется с помощью алгоритма, встречается несколько подстрок, то применяться будет формула, имеющая минимальный номер.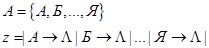
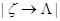 , где
, где 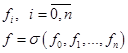
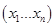 не используется для вычисления какой-то из функций, то для этой функции мы объявляем этот элемент не значащим.
не используется для вычисления какой-то из функций, то для этой функции мы объявляем этот элемент не значащим.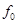 будут результаты вычисления
будут результаты вычисления 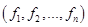 для набора
для набора 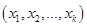
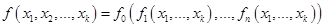 , где
, где 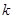 - количество переменных в объединенном наборе переменных функций с индексами от 1 до
- количество переменных в объединенном наборе переменных функций с индексами от 1 до 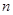 .
.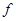 не будет определена в двух случаях:
не будет определена в двух случаях: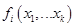 не определено
не определено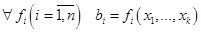 , но при этом
, но при этом 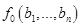 не определено
не определено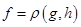
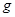 , зависит от
, зависит от 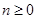 , а второй операнд, функция
, а второй операнд, функция 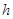 , в общем случае имеет на два дополнительных аргумента. Функция – результат
, в общем случае имеет на два дополнительных аргумента. Функция – результат 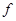 определяется следующими уравнениями примитивной рекурсии:
определяется следующими уравнениями примитивной рекурсии: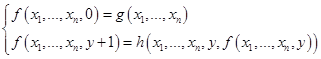
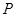 с помощью операций суперпозиции и примитивной рекурсии, называется примитивно рекурсивными функциями
с помощью операций суперпозиции и примитивной рекурсии, называется примитивно рекурсивными функциями 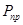 . Все примитивно рекурсивные функции всюду вычислимы. Для того чтобы расширить набор следовало бы, кроме примитивной рекурсии ввести еще и кратную рекурсию, определить косвенную рекурсию.
. Все примитивно рекурсивные функции всюду вычислимы. Для того чтобы расширить набор следовало бы, кроме примитивной рекурсии ввести еще и кратную рекурсию, определить косвенную рекурсию.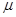 имеет один операнд,
имеет один операнд, 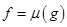 . Значения функции
. Значения функции 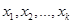 получаются следующим образом. Сначала с помощью функции
получаются следующим образом. Сначала с помощью функции 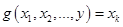 , а затем отыскивается его решение
, а затем отыскивается его решение 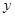 . Если таких решений несколько, то берется минимальное из них; оно и считается значением функции
. Если таких решений несколько, то берется минимальное из них; оно и считается значением функции 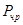 .
.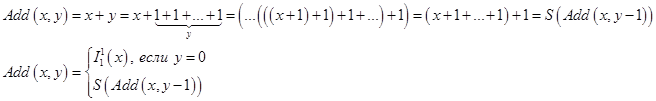 2)
2)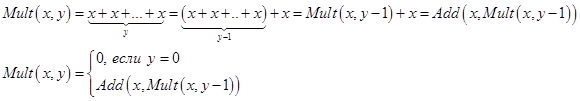
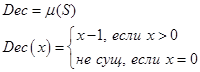
 Проблема алгоритмической разрешимости. Примеры неразрешимых алгоритмических проблем.
Проблема алгоритмической разрешимости. Примеры неразрешимых алгоритмических проблем. Методы разработки алгоритмов. Суперпозиция, итерация, рекурсия.
Методы разработки алгоритмов. Суперпозиция, итерация, рекурсия.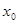 , близкое к решению. Далее это решение «уточняется». Чаще всего абсолютная точность недостижима, поэтому процесс потенциально бесконечен. Для того чтобы этого избежать, несколько изменяют начальную формулировку задачи: требуется отыскать не точное решение, а приближенное.
, близкое к решению. Далее это решение «уточняется». Чаще всего абсолютная точность недостижима, поэтому процесс потенциально бесконечен. Для того чтобы этого избежать, несколько изменяют начальную формулировку задачи: требуется отыскать не точное решение, а приближенное. Технологии разработки программ. Технологии и методы тестирования программ.
Технологии разработки программ. Технологии и методы тестирования программ. Рекурсивные алгоритмы: определение и виды рекурсии. Реализация рекурсии и использование стека. Рекурсия и итерация. Примеры, сравнение.
Рекурсивные алгоритмы: определение и виды рекурсии. Реализация рекурсии и использование стека. Рекурсия и итерация. Примеры, сравнение.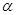 называется рекурсивным, если:
называется рекурсивным, если: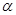 к себе. Под обращением будем понимать передачу управления или вызов. В этом случае речь идет о прямой рекурсии.
к себе. Под обращением будем понимать передачу управления или вызов. В этом случае речь идет о прямой рекурсии.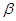 , который в свою очередь вызывает
, который в свою очередь вызывает 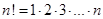 , причем
, причем 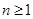 и
и 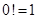
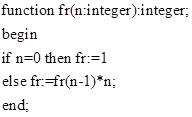
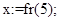
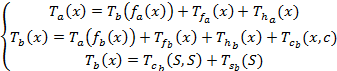
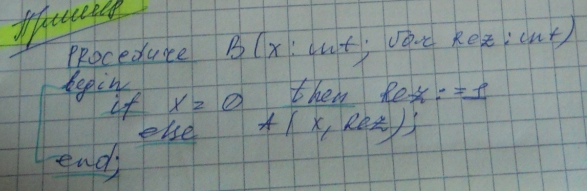

 Оптимизация алгоритмов. Примеры.
Оптимизация алгоритмов. Примеры.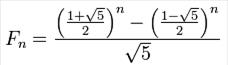
 Понятие сложности задачи и классы сложности задач. Понятия сводимости, полиномиальная сводимость.
Понятие сложности задачи и классы сложности задач. Понятия сводимости, полиномиальная сводимость.
 Методы сортировок: сортировка массивов простыми включениями, сортировка массивов простым выбором, сортировка обменами. Анализ сложности алгоритмов сортировки.
Методы сортировок: сортировка массивов простыми включениями, сортировка массивов простым выбором, сортировка обменами. Анализ сложности алгоритмов сортировки.
 Алгоритмы внешней сортировки: метод естественного слияния, метод сбалансированного слияния. Двухпутевая и многопутевая реализация. Фибоначчиева сортировка.
Алгоритмы внешней сортировки: метод естественного слияния, метод сбалансированного слияния. Двухпутевая и многопутевая реализация. Фибоначчиева сортировка.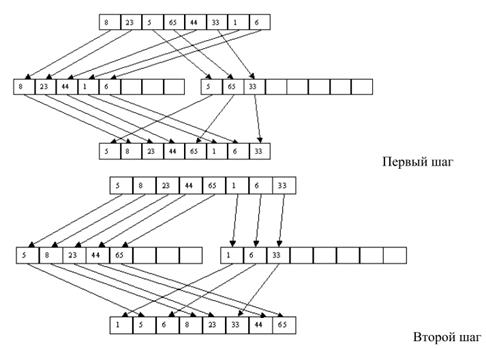
 Понятие хеширования. Построение хеш функции. Разрешение коллизий, линейное рехеширование, случайное рехеширование, квадратичное рехеширование, метод цепочек (списковое и матричное представление)
Понятие хеширования. Построение хеш функции. Разрешение коллизий, линейное рехеширование, случайное рехеширование, квадратичное рехеширование, метод цепочек (списковое и матричное представление)


