
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение рекурсии и итерации
Рекурсия:
При прямом ходе вычисление значения функции откладывалось, при этом значение функции для одного аргумента заменялось на значение выражения, в котором нужно было вычислить значение той же функции, но для другого аргумента. Вычисляемая функция откладывалась до тех пор, пока в выражении не появится значение функции, которое было определено. После подстановки известного значения, происходил возврат к отложенным вычислениям.
Итерация:
После определения начального значения
При выполнении сравнения можно учитывать разные критерии. 1. Самый распространенный – это эффективность алгоритма. В данном случае под эффективность понимаются время процессора и объем занятой программой (и данными) памяти. В данном случае не трудно заметить явное преимущество итеративного метода по сравнению с рекурсивным. 2. Сложность написания и отладки программы. По существу это вопрос о затратах труда программиста. Сравнение двух текстов показывает, что рекурсивная программа пишется автоматически на основе поставленной задачи, в то время как итеративная требует преобразования задачи и "изобретения" алгоритма, введение дополнительных переменных, отсутствовавших в постановке задачи, и неочевидных операций. Поэтому, с этой точки зрения, рекурсивный алгоритм предпочтительнее итеративного. Вывод: В тех случаях, когда не требуется получать очень быстрый отклик программы, рекурсия помогает сэкономить на разработке программы. на примере чисел Фибоначчи: рекурсия: function Fr(n:integer):integer; begin if n=1 or n=2 then Fr:=1 else Fr:=Fr(n-1)+Fr(n-2); end; итерация: function Fi(n:integer):integer; var i,n1,n2,result: integer; begin n1:=1,n2:=1;{установка начальных значений} result:=1; {на тот случай,если n=1 или 2} for i:=3 to n do {не выполняется если n<3} begin result:=n1+n2; {соот-ет осн формуле чисел Фиб} n2:=n1; {сдвиг значений на один индекс} n1:=result; {----||----} end; Fi:=result; {установление значения функции} end;
9) Задача анализа сложности алгоритмов. Временная и емкостная сложности. Использование управляющего графа для оценки сложности линейных и ветвящихся алгоритмов.
Сложность алгоритма определяется в двух аспектах: сложность по памяти и сложность по времени исполнения. Емкостная сложность алгоритма определяет, насколько много памяти требуется для выполнения этого алгоритма. Временная сложность алгоритма определяет, насколько много процессорного времени требует алгоритм для своего выполнения.
Оценка временной сложности. Рассчитывается в относительных единицах так, чтобы эта оценка, по возможности, была одинаковой для компьютеров с разной тактовой частотой, а именно в количестве исполняемых операций. Рассмотрим подробно список операций, учитываемых при подсчете временной сложности (каждая из перечисленных операций принимается с весом равным 1) · арифметические операции (+,–,*,/,div, mod); · унарный минус (–); · операция пересылки, возникающая при выполнении оператора присваивания (:=); · операции сравнения (>,<,=,<=,<=,<>); · логические и побитовые операции (not, and, or, xor, shr, shl); · выполнение стандартных функций (inc(), dec(), abs(), sin(), cos(), exp(), ln(), arctan(), sqr(), sqrt(), int(), frac(), round(), trunc(), odd(), chr(), ord(), pred(), succ(), upcase(), high(), low()); · операции ввода-вывода одной переменной (read(), readln(), write(), writeln()). Оценка емкостной сложности. Учет памяти обычно ведётся по объёму данных и не принимается во внимание память, расходуемая для записи команд программы. Обозначим временную сложность алгоритма a через Sa. Емкостную сложность будем подсчитывать в относительных единицах, не зависящих от языка программирования и компьютера на котором происходит выполнение программы, а именно в количестве скалярных переменных, описанных в программе. Под скалярными переменными будем понимать переменные и константы простых (скалярных) типов данных. Напомним, что к простым (скалярным) типам данных в Паскале относятся: · все числовые типы (целые – Integer, Byte, Word, ShortInt, LongInt; вещественные – Real, Single, Double, Extended); · символьный тип (Char); · логический тип (Boolean); · перечислимый тип; · интервальный тип. · массив емкостная сложность определяется числом элементов массива · строковый тип емкостная сложность на единицу больше числа символов максимально допустимых в строке
· запись емкостная сложность равна сумме емкостных сложностей полей записи
Для многих задач возможно найти только верхнюю (Tmax) или нижнюю (Tmin) оценку сложности алгоритма, а также среднюю (Taverage) оценку. Для нахождения верхней оценки оценивается количество необходимых операций в худшем случае, то есть для набора исходных данных, требующих максимального количества операций обработки. Для нахождения нижней оценки ищется сложность для набора данных, требующего минимального количества операций.
Отыскание функции сложности производится на основе анализа текста алгоритма. С целью анализа алгоритм удобно представлять управляющим графом. В нём каждому оператору или вызову процедуры ставится в соответствие вершина графа (точка).
Каждой вершине графа припишем число – количество операций, которые необходимо выполнить для исполнения оператора программы, связанного с этой вершиной. Это число назовём весом вершины. Вес пустой, начальной и заключительных вершин равен 0.
1. Управляющий граф представляет собой линейный участок. Сложность равна сумме весов вершин, принадлежащих линейному участку. Если на участке нет вершин – вызовов процедур, то сложность является константой.
Пример: Рассмотрим фрагмент алгоритма: a:= y + r; Proc(a,y); b:=4*d – 10 mod b; Известно, что сложность процедуры Proc равна 2V+1. Построим управляющий граф, снизу от каждой вершины графа напишем ее вес.
Ta(V)=2V+7. 2. Управляющий граф содержит разветвления, но не содержит циклов. Расчёт сложности зависит от того, рассматриваем мы худший, лучший или средний случай. Поскольку для вычисления средней оценки сложности используется вероятностный подход, приведем начальные понятия из теории вероятности: · Вероятность события (p) есть объективная мера возможности события, выражаемая числом, удовлетворяющим условию 0 ≤ p ≤ 1. · Достоверное событие, т.е. то событие, которое непременно произойдет, имеет вероятность равную 1. · Невозможное событие имеет вероятность равную 0.
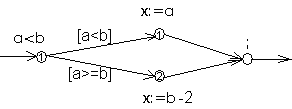
Пример: Рассмотрим фрагмент алгоритма: If a < b then x:= a else x:= b -2; Известно, что вероятность выполнения условия a<b равна Построим управляющий граф, внутри каждой вершины графа напишем ее вес.
Вычислим веса ветвей T1 = 1+1+0 = 2, T2 = 1+2+0 = 3. Tmin = 2, Tmax = 3. Для определения средней оценки сложности вычислим вероятности выполнения ветвей. p1 = p2 = 1 – p1 = Taverage = p1T1+p2T2 =
10) Управляющий граф содержит цикл, но не содержит вложенных циклов. В этом случае, временная сложность зависит от количества повторений цикла. Введем обозначения: Tтела цикла – временная сложность операторов, выполняемых в теле цикла; Tусловия – количество операций, выполняемых при проверке условия цикла; k – количество повторений тела цикла; T(k) – временная сложность выполнения цикла, как функция, зависящая от параметра k. Рассмотрим часто встречающиеся случаи: 1) Цикл с параметром c заголовком for i:=1 to n do k = n, T(k) = k∙Tтела цикла. 2) Цикл с параметром с заголовком в общем виде for i:= a to b do k = (b–a)+1, T(k) = k∙Tтела цикла. 3) Цикл с предусловием While … Do. Условие в таком цикле всегда проверяется на 1 раз больше по сравнению с количеством выполнений тела цикла.
T(k) = (k+1) ∙Tусловия + k∙Tтела цикла, k ≥ 0. 4) Цикл с постусловием Repeat … Until. Количество выполнений тела цикла совпадает с количеством проверок условия цикла, минимально тела цикла выполняется 1 раз. T(k) = k ∙Tусловия + k∙Tтела цикла, k ≥ 1. В случае, когда число повторений цикла равно константе, нижняя, верхняя и средняя оценки сложности совпадают, и их вычисление не требует особых пояснений. Рассмотрим случай, когда число повторений цикла является переменной величиной. В этом случае: – Нижняя оценка сложности Tmin соответствует случаю, когда тело цикла выполняется минимально возможное число раз, обозначим это число kmin. – Верхняя оценка сложности Tmax соответствует случаю, когда тело цикла выполняется максимально возможное число раз, обозначим это число kmax. – Средняя оценка сложности вычисляется как сумма произведений вероятности того, что цикл выполнится k раз, на сложность алгоритма при k итерациях цикла, при этом значение k последовательно пробегает все значения от kmin до kmax. Taverage =
Пример: Рассмотрим фрагмент алгоритма, в котором n – целое число, n x:=0; For i:=1 to n do x:=x+i; Построим управляющий граф, внутри каждой вершины графа напишем ее вес.
Функция сложности T(k) = 1+2k. Поскольку количество повторений тела цикла k=n, можно переписать функцию сложности по-другому T(n) = 1+2n. Таким образом, параметром V, характеризующим сложность входных данных, является n (V=n). Минимально цикл выполняется 0 раз, следовательно, Tmin = T(0) = 1. Максимально возможное число повторений тела цикла равно 10, значит Tmax=T(10)=1+2∙10=21. Поскольку все значения n равновероятны p0 = p1 = … = p10 = Tavareage = Управляющий граф содержит вложенные циклы. Возможно два случая:
|
|||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.251.72 (0.038 с.) |
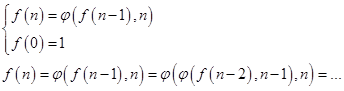
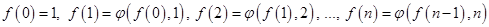
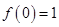 , повторяются одни и те же действия, при которых, значения, полученные на предыдущем шаге, используются для вычисления очередного значения функции.
, повторяются одни и те же действия, при которых, значения, полученные на предыдущем шаге, используются для вычисления очередного значения функции.
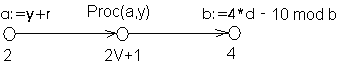
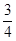 .
.
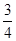 по условию,
по условию,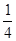 , т.к. события «выполнилась 1 ветвь» и «выполнилась 2 ветвь» несовместны и образуют полную группу.
, т.к. события «выполнилась 1 ветвь» и «выполнилась 2 ветвь» несовместны и образуют полную группу.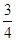 ·2+
·2+  Оценка сложности циклических алгоритмов. Примеры.
Оценка сложности циклических алгоритмов. Примеры.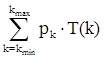
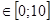 и все значения n равновероятны.
и все значения n равновероятны.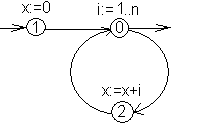
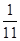 .
.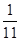 ∙T(0) +
∙T(0) + 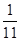 ∙
∙ 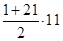 = 11.
= 11.


