Сортировка фон Неймана (слиянием)

Метод основан на идее слияния двух отсортированных частей массива, поэтому первоначально массив разбивается на две части, которые независимо сортируются, а затем результаты сливаются в единое целое. С каждой из частей выполняются аналогичные действия, до тех пор, пока количество элементов в сортируемой части массива не станет равно двум. В этом случае выполняется простое сравнение элементов и их перестановка, если она необходима.

 

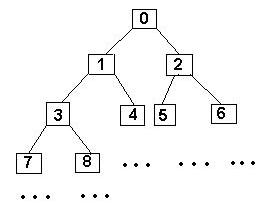
Пирамидальная сортировка:

1. Построение пирамиды
Пирамида представляет собой дерево, в котором каждый узел имеет не более двух потомков, причем узел всегда больше или равен своим потомкам (таким образом, на вершине дерева всегда находится наибольший элемент).

Если в исходном массиве n элементов, то последние (n / 2) элемента становятся основанием пирамиды (эти элементы являются листьями дерева, т.е. у них нет потомков, поэтому для них вышеуказанное правило выполняется автоматически).

Удобнее всего поместить пирамиду в массив. При этом распределение индексов массива по узлам дерева будет выглядеть так (на этом рисунке все цифры - это индексы элементов массива, а ни в коем случае не значения этих элементов):

Таким образом, для того, чтобы каждый узел дерева был больше своих потомков, каждый элемент массива a[i] должен быть больше или равен элементам a[2 * i + 1] и a[2 * i + 2].

2. Сортировка
В этой части алгоритма мы перемещаем в конец массива максимальный элемент, затем исключаем его из дальнейшего процесса сортировки. Поскольку максимальный элемент всегда находится на вершине пирамиды, мы должны поменять местами элементы a[0] и a[n-1] (т.е. последний элемент). Причем элемент a[n-1] необходимо добавлять так, чтобы не нарушился порядок пирамиды (при этом пирамиду придется частично перестроить). Далее мы будем рассматривать массив только до (n-2)-го элемента.
На следующем шаге мы меняем местами a[0] и a[n-2] и далее рассматриваем массив только до (n-3)-го элемента. Повторяем всю эту процедуру до тех пор, пока в рассматриваемой части массива не останется один элемент.

Шейкер сортировка:

Это модификация метода «пузырька», которая учитывает два дополнительных требования:

1) устранение «лишних» просмотров массива, т.е. если массив уже отсортирован за первые проходы, последующие проходы не делаем. Пример: 12,3,5,7,9,10.

2) смена направлений прохода массива: сначала проходим от начала к концу, по том – от конца к началу, потом снова от начала к концу и т.д. Это позволяет уменьшить число проходов по массиву. Пример: 5,7,9,10,12,3.

 

Сортировка подсчетом:

Идея алгоритма состоит в том, чтобы для каждого элемента x предварительно подсчитать, сколько элементов входной последовательности меньше x. После этого х записывается напрямую в выходной массив в соответствии с этим числом. Например, если семнадцать элементов входного массива меньше х, то в выходном массиве х должен быть записан на место с номером восемнадцать.

Используются следующие обозначения:
A[1..n] - входная последовательность;
C[1..k] - вспомогательный массив из k элементов;
B[1..n] - выходная отсортированная последовательность.

Работа алгоритма заключается в следующем.
В элемент C[i] заносится количество элементов массива A, равных i.
Затем находятся частичные суммы последовательности C[1], C[2],..., C[k], каждая из которых является количеством элементов, не превосходящих i.
После этого каждый элемент A[i] из входного массива помещается в выходной массив B на позицию, равную значению элемента С[A[i]].

 

Цифровая сортировка:

Этой сортировкой можно сортировать целые неотрицательные числа большого диапазона. Идея состоит в следующем: отсортировать числа по младшему разряду, потом устойчивой сортировкой сортируем по второму, третьему, и так до старшего разряда.

 

                             

17)  Методы поиска: линейный поиск, метод бинарного писка, поиск с помощью бинарного дерева, метод случайного поиска.

 

Линейный, последовательный поиск — алгоритм нахождения заданного значения произвольной функции на некотором отрезке. Данный алгоритм является простейшим алгоритмом поиска и в отличие, например, от двоичного поиска, не накладывает никаких ограничений на функцию и имеет простейшую реализацию. Поиск значения функции осуществляется простым сравнением очередного рассматриваемого значения (как правило поиск происходит слева направо, то есть от меньших значений аргумента к большим) и, если значения совпадают (с той или иной точностью), то поиск считается завершённым.

 

Бинарный поиск –

Если у нас есть массив, содержащий упорядоченную последовательность данных, то очень эффективен двоичный поиск.

Переменные Lb и Ub содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Мы начинаем всегда с исследования среднего элемента отрезка. Если искомое значение меньше среднего элемента, мы переходим к поиску в верхней половине отрезка, где все элементы меньше только что проверенного. Другими словами, значением Ub становится (M – 1) и на следующей итерации мы работаем с половиной массива. Таким образом, в результате каждой проверки мы вдвое сужаем область поиска. Так, в нашем примере, после первой итерации область поиска – всего лишь три элемента, после второй остается всего лишь один элемент. Таким образом, если длина массива равна 6, нам достаточно трех итераций, чтобы найти нужное число.