
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сортировка методом простых вставок (метод прямого (простого) включения)Содержание книги
Поиск на нашем сайте 1) Начиная со 2-го элемента, каждый текущий элемент с номером k запоминается в промежуточной переменной. 2) Затем просматриваются предыдущие k –1 элемент и ищется место вставки k -го элемента таким образом, чтобы не нарушить упорядоченности, при этом все элементы, превышающие k - й,сдвигаются вправо. 3) На освободившееся место вставляется k -й элемент.
const NMAX =10; type item=record key: integer; {ключ, по которому сортируется массив} {сопутствующие элементы структуры записей} end; TMassiv= array [0..NMAX] of item; Proсedure Sort_Insert(n:word; Var a:TMassiv); Var i,j:word; x:item; BEGIN For i:=2 To n Dobеgin x:= a [ i ]; {передвигаемый в левую часть элемент} a [0]:= x; {фиктивный элемент – «барьер», установлен на тот случай, когда a [ i ] должен переместиться на первое место } j:= i -1; {правый край левой части} While x.k е y<a[j].key Dobеgin a [ j +1]:= a [ j ]; j:= j -1; {продвижение «дырки» в левой части массива справа налево до той позиции, в которую должен быть включен элемент a [ i ] } end; a [ j +1]:= x {включение a [ i ] в «дырку» в левой части } еnd END; Сложность: Количество элементарных операций зависит, в первую очередь, от размера сортируемого массива. Однако величина n не определяет это количество однозначно. Для различных массивов одного и того же размера тело цикла While x. key < a [ j ]. key Do будет выполняться различное число раз. Поэтому необходимы три оценки сложности: минимальная, максимальная и средняя. Минимальная сложность получается в том случае, когда элементы упорядочиваемого массива уже располагаются в нужном порядке. Тогда проверки x. key < a [ j ]. key всегда будут давать отрицательный результат и тело цикла не выполнится ни разу. И выполнение процедуры сведется к выполнению следующих операторов: For i:=2 To n Dobеgin x:=a[i]; a[0]:=x; j:=i-1; а [j+1]:=x еnd Тело цикла For исполняется точно n -1 раз, и число пересылок записей (присваиваний): Mmin =3(n -1). Число сравнений ключей: Cmin = n -1. Максимальная сложность получается в том случае, когда элементы исходного массива расположены в порядке убывания. Тело цикла While выполняется до тех пор, пока элемент х не натолкнется на барьер, т.е. при i =2 один раз, при i =3 два раза; при i = n выполнится (n -1) раз. Количество пересылок записей: Mmax =3(n -1)+ =3(n-1)+(1+2+...+n-1)=3(n-1)+n(n-1)/2=(6n-6+n2-n)/2= =(n2+5n-6)/2. Количество сравнений: Cm ах =2+3+…+ n =(n +2)(n -1)/2= =(n 2 - n +2 n -2)/2=(n 2 + n -2)/2. Средняя оценка сложности получится, если предположить, что все элементы исходного массива – случайные числа. Результат очередной проверки в операторе While также является случайным, т.е. не можем сказать, сколько раз выполнится тело цикла. Структуру процедуры с точки зрения анализа сложности можно переписать так: For i:=2 To n Do begin 2 пересылки записей случайное число пересылок 1 пересылка записи end Математическое ожидание количества пересылок в цикле While при условии, что новый элемент вставляется в уже отсортированную последовательность длиной i равна i /2, т.е. в среднем придется просмотреть половину последовательности, до тех пор, пока не найдется подходящее место. Получается, что в начале работы алгоритма сортировки вставками (начинаем с i =2) у нас имеется отсортированная последовательность из одного элемента, количество перестановок может быть либо 1 (1-й элемент меняем местами со 2‑м элементом), либо 0 (т.к. 2-й элемент уже находится на своем месте). При i =3 (длина отсортированной последовательности равна двум) возможны три варианта: 0 пересылок, 1 пересылка, 2 пересылки. По определению математического ожидания количество пересылок равно 1. Таким образом, при i = n (длина отсортированной последовательности равна n –1) количество пересылок может быть от 0 до n –1. Математическое ожидание количества пересылок при условии, что в среднем придется просмотреть половину последовательности из n –1 элемента, будет равно (n ‑1)/2. Тогда M ср =3(n -1)+ =3(n-1)+1/2·n·(n-1)/2=3(n-1)+(n2-n)/4= =3n-3+(n2-n)/4=(12n-12+n2-n)/4= =(n 2 +11 n -12)/4.
15)
Алгоритм: · выбрать элемент, называемый опорным. · сравнить все остальные элементы с опорным, на основании сравнения разбить множество на три — «меньшие опорного», «равные» и «большие», расположить их в порядке меньшие-равные-большие. · повторить рекурсивно для «меньших» и «больших».
procedure hoarsort(var mas: array[1..100] of integer; a,b:integer);//при начальном вызове a=1 b=количеству элементов массива var i,j,m,k:integer; begin i:=a; j:=b; if (a>=b) then else begin m:=mas[(a+b)div 2]; while i<=j do begin while mas[i]>m do inc(i); while mas[j]<m do j:=j-1; if i<=j then begin k:=mas[i]; mas[i]:=mas[j]; mas[j]:=k; inc(i); j:=j-1; end; end; hoarsort(mas,a,j); hoarsort(mas,i,b); end; end;
+ оценка сложности
16)
Сортировка Шелла: Идея метода: делим массив на k1 групп, каждую группу сортируем, далее делим массив на k2 групп (k2<k1), снова сортируем полученные группы, далее на k3 групп (k3<k2<k1), и т.д. в конце делим на kn групп, причем kn = 1, т.е. в конце сортируем весь массив. Значения k1, k2, k3, …, kn называются приращениями.
Лучшим считается выбор в качестве значений приращений взаимно простых чисел.
|
||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

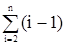 =
=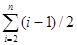 =3(n -1)+1/2(1+2+...+(n -1))=
=3(n -1)+1/2(1+2+...+(n -1))= Методы сортировок: алгоритм быстрой сортировки. Анализ сложности алгоритма быстрой сортировки.
Методы сортировок: алгоритм быстрой сортировки. Анализ сложности алгоритма быстрой сортировки. Обзор методов сортировок: Сортировка Шелла, пирамидальная сортировка, сортировка слияниями, Шейкер – сортировка, сортировка подсчетом, цифровая сортировка...
Обзор методов сортировок: Сортировка Шелла, пирамидальная сортировка, сортировка слияниями, Шейкер – сортировка, сортировка подсчетом, цифровая сортировка...


