
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Количество повторений вложенного цикла не зависит от параметра внешнего циклаСодержание книги
Поиск на нашем сайте
Построить функцию сложности итеративного алгоритма умножения двух квадратных матриц А = {aij} и B = {bij} размера n x n, результатом которого является матрица C = {cij}, также размером n x n. procedure MULTIPLY (n: integer; a, b: matrix; var c: matrix); var i, j, k: integer; Begin for i:= 1 to n do {Цикл 1} for j:= 1 to n do {Цикл 2 и начало тела цикла 1} begin c [ i, j ]:= 0; {Начало тела цикла 2} for k:= 1 to n do {Цикл 3} c[i, j]:= c[i, j] + a[i, k] * b[k, j]; {Тело цикла 3} end {Конец тела цикла 2; конец тела цикла 1} end; Тип данных matrix определен вне процедуры как двумерный массив. Время доступа к элементам не учитываются при анализе алгоритмов. Прежде всего, выберем параметр V. Простой анализ текста показывает, что за параметр сложности данных можно взять размер n матриц, участвующих в вычислениях. Поскольку процедура представляет собой цикл по переменной i, то ее временная сложность Т α (n) = n· T (1). В свою очередь, T (1) = n· T ( 2 ) и, следовательно, Т α (n) = n·(n· T ( 2 )). Тело цикла 2 состоит из одного оператора присваивания и цикла 3. Таким образом, Т α (n) = n·(n·(1 + n· T ( 3 ))). Тело цикла 3 включает умножение, сложение и присваивание (3 операции). Окончательно получаем Т α (n) = n ·(n ·(1 + n ·3)) = 3 n 3 + n 2 Количество повторений вложенного цикла зависит от параметра внешнего цикла Введем следующие обозначения: k - количество повторений внешнего цикла. В примере k=n. f(k) – функция зависимости количества повторений вложенного цикла от числа повторений внешнего цикла. В примере f(1)=1, f(2)=2, …, f(n)=n. T(1), T(2) - временная сложность тела цикла 1-го (верхнего) уровня и 2-го уровня (вложенного цикла) соответственно. В примере T(2) = 2. a(1) - временная сложность операторов, предшествующих вложенному оператору цикла, в теле цикла верхнего уровня. В примере a(1) = 1. b(1) - временная сложность операторов, следующих после вложенного оператора цикла, в теле цикла верхнего уровня. В примере b(1) = 2. T – временная сложность всего алгоритма. a – временная сложность операторов, предшествующих циклу, в основном алгоритме. В примере a=1. b – временная сложность операторов, следующих после цикла в основном алгоритме. В примере b=1. T = a+b+k∙(a(1) +b(1)) + T(2)∙
11) Под рекурсией понимается метод определения функции через её предыдущие и ранее определенные значения, а так же способ организации вычислений, при котором функция вызывает сама себя с другим аргументом. При прямой рекурсии процедура содержит вызов себя в собственном теле, например: procedure процедура _1 …. if … then процедура _1 …. end; Косвенная рекурсия образуется цепочкой процедур, и эта цепочка замыкает себя в рекурсивное кольцо, например: procedure процедура_1 …. … процедура_2 …. end; procedure процедура_2 …. … процедура_3 …. end; procedure процедура_3 …. … процедура_1 End;
· Для вычисления сложности рекурсивных алгоритмов используется рекуррентное уравнение: T a (X)=T a (f(X))+ Tf(X)+ Th(X)+ Tс (X,S) T a (S)=Tc(S,S)+ Ts(S) Здесь T a(X) – общая сложность рекурсивного алгоритма T a(f(X)) – сложность предыдущего уровня рекурсии Tf(X) – сложность вычисления аргументов при рекурсивном вызове процедуры Th(X) – сложность нерекурсивных вычислений Tс(X, S) – сложность операции сравнения Ts(S) – сложность вычисления нерекурсивного начального значения Tc(S, S) – сложность операции сравнения для нерекурсивного начального значения Пример: Function F(n); begin If (n=0) or (n=1) {проверка возможности прямого вычисления} Then F:= 1 Else F:=n*F(n-1); {рекурсивный вызов функции} End; X = x, S = 1, x = 1 f(X)=X-1, FACTORIAL (x-1) Tf(X)=1, FACTORIAL (x-1) Th(X) = 2, FACTORIAL:= x * FACTORIAL (x-1) Tc(X,S)=l, x = 1 Ts(S) = 1. FACTORIAL:= 1 Таким образом, система уравнений превращается в Тa(x) = Тa(х-1)+4, Тa(1) = 2. Ее решение – Тa(x) = 4х-2.
В случае косвенной рекурсии рекуррентное уравнение имеет вид:
12) Поиск алгоритма min сложности – оптимизация алгоритма.
Одна из задач, которая обычно ставится при разработке алгоритмов и программ - минимизация требуемых программой ресурсов. Особенно это касается системного программного обеспечения: программ операционной системы, трансляторов, систем управления базами данных и знаний и т. д., т.е. программ, имеющих большое количество пользователей и испытывающих как товар, большую конкуренцию на рынке программных средств.
Существует несколько самостоятельных аспектов оптимизации программ, из которых выделим два: · оптимизация, связанная с выбором метода построения алгоритма; · оптимизация, связанная с выбором методов представления данных в программе.
Первый вид оптимизации имеет глобальный характер и (при удачной оптимизации) ведет к уменьшению порядка функции сложности - например, замена алгоритма с Т a (V) = O(FS) на алгоритм с T a (V) = O(V4). Он зависит от того, как задача разбивается на подзадачи, насколько это разбиение свойственно самой задаче или является только искусственным приемом.
Второй вид оптимизации, не меняя структуры программы в целом, ведет к экономии памяти и/или упрощению работы со структурами данных, повышению эффективности вспомогательных процедур, обеспечивающих "интерфейс" между прикладным уровнем (на котором мыслим в терминах высокоуровневых объектов - графов, матриц, текстов и т. д.) и машинным уровнем, поддерживающим простейшие типы данных (числа, символы, указатели). Результатом этого обычно является уменьшение коэффициентов при некоторых слагаемых в функции сложности (при удачной оптимизации - при наиболее значимом слагаемом), но порядок функции сложности остается тем же.
Пример: вычисления числа Фибоначчи через формулу:
13) Задачи:
сложность задачи – сложность самого простого алгоритма. Поиск алгоритма min сложности – оптимизация алгоритма. Детерминированные вычисления – обычный, классический способ. Недетерминированные вычисления – существует в нескольких параллельно работающих экземплярах. Недетерминированный вычислитель исполняет недетерминированные алгоритмы. Разрешаем шаги с неоднозначным результатом – шаги, вырабатывающие сразу несколько значений для одной переменной. Эти значения могут использоваться:
Классы сложности задач:
Задача Q сводится к задаче Р за полином.время, если сущ-ет детерминированный полиномиальный алгоритм, преобразовывающий произвольный частный случай задачи Р так, что ответом для данного случая задачи Q является «да» тогда и только тогда,када ответом на соответсвующий случай задачи Р также является «да». вход для Q Вход для Р ответ Р Ответ Q
Полиномиальная сводимость – детерминированный полиномиальный алгоритм сводит одну задачу к другой NPC – подкласс NP, любая задача NP сводится к ним
14) Сортировка – процесс перегруппировки заданного множества объектов в некотором определенном порядке. Цель сортировки – облегчить последующий поиск элементов в таком упорядоченном (отсортированном) множестве. Сортировку массивов называют внутренней сортировкой, т.к. поскольку массивы хранятся в быстрой, оперативной, внутренней памяти ЭВМ, допускающей случайный (прямой) доступ к элементам. При анализе сложности алгоритмов сортировки будем учитывать только операции сравнения и пересылки записей.
Сортировка обменами: Производится последовательное упорядочение смежных пар элементов массива: x [1] и x [2], x [2] и x [3], … x [ N -1] и x [ N ]. Если первый элемент больше второго, то элементы переставляются. В итоге, после N –1 сравнения максимальное значение переместится на место элемента X [ N ], т.е. "вверху" оказывается самый "легкий" элемент – отсюда аналогия с пузырьком. Следующий проход делается до второго сверху элемента (X [ N –1]), таким образом второй по величине элемент поднимается на правильную позицию и т.д. Таким образом, нужно выполнить данную процедуру N –1 раз. При первом прохождении нужно сравнить N –1 пар элементов, при втором – N –2 пары, при k -м прохождении – N ‑ k пар.
Program Sort1; Const N=10; Type mas=array[1..N] of real; Var x:mas; i,k:integer; a:real; Begin For i:=1 to N do {Ввод элементов массива} read(x[i]); For i:=1 to N-1 do {Сортировка} For j:=1 to N-i do If x[j]>x[j+1] then Begin a:=x[j]; x[j]:=x[j+1]; x[j+1]:=a; End; For i:=1 to N do {Вывод элементов массива} Write(x[i],’ ‘) End. Среднее число сравнений и обменов имеют квадратичный порядок роста: О (n 2), отсюда можно заключить, что алгоритм пузырька очень медленен и малоэффективен.
|
||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.195.8 (0.007 с.) |

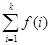
 Оценка сложности рекурсивных алгоритмов: рекурсия с 1 и многими рекурсивными вызовами, случай косвенной рекурсии.
Оценка сложности рекурсивных алгоритмов: рекурсия с 1 и многими рекурсивными вызовами, случай косвенной рекурсии.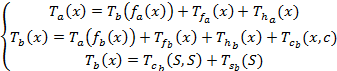
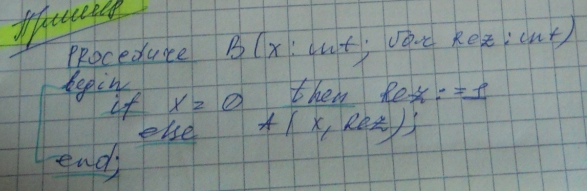

 Оптимизация алгоритмов. Примеры.
Оптимизация алгоритмов. Примеры.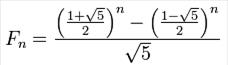
 Понятие сложности задачи и классы сложности задач. Понятия сводимости, полиномиальная сводимость.
Понятие сложности задачи и классы сложности задач. Понятия сводимости, полиномиальная сводимость.
 Методы сортировок: сортировка массивов простыми включениями, сортировка массивов простым выбором, сортировка обменами. Анализ сложности алгоритмов сортировки.
Методы сортировок: сортировка массивов простыми включениями, сортировка массивов простым выбором, сортировка обменами. Анализ сложности алгоритмов сортировки.


