
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика расчета генератора твердотельного лазера с накачкой диодными матрицами.Содержание книги
Поиск на нашем сайте
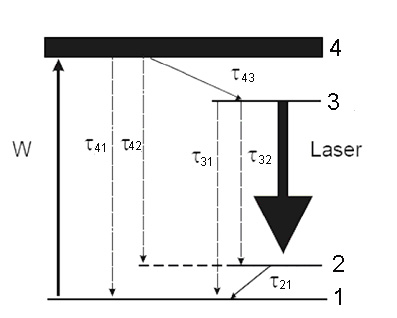
Расчет лазерного генератора заключается в последовательном расчете накачки, усиления в резонаторе и теплового расчета. Рассматриваемый нами лазер на гранате с неодимом работает по так называемой четырехуровневой схеме [38]. Схема основных энергетических уровней ионов неодима в матрице иттрий алюминиевого граната, участвующих в процессах накачки и генерации, приведена на рисунке 32а.
Рисунок32а - Схема энергетических уровней ионов неодима в матрице Y3Al5O12 Первый уровень, называемый основным, соответствует минимально возможному значению энергии, которую могут иметь ионы неодима. Число ионов, имеющих минимальную энергию (находящихся на основном уровне), составляет большинство. Число ионов, находящихся на более высоких уровнях энергии, заметно меньше и оно подчиняется равновесному распределению Больцмана:
Предположим, что внутри кристалла распространяется свет с частотой, равной частоте перехода между рабочими уровнями 2 и 3. Он вызывает два процесса: вынужденного излучения ионов неодима, находящихся на уровне 3, и при этом к волне добавляется энергия излучения (усиление света), и процесс поглощения энергии волны ионами, находящимися на уровне 2 (рисунок 32а). В нормальном состоянии число ионов на уровне 2 больше, чем на уровне 3, и поглощение волны превалирует над усилением, то есть свет ослабляется. Если кристалл облучается светом накачки, то под его воздействием ионы неодима сначала переходят на уровни (полосы) накачки 4, а затем быстро на метастабильный уровень 3, где задерживаются. При достаточной мощности накачки скорость поступления ионов на метастабильный уровень превысит скорость ухода их с этого уровня за счет спонтанных переходов. В этом случае будет происходить накопление ионов на метастабильном уровне и через какое-то время число ионов на уровне 3 превысит число ионов на уровне 2. В этом случае излучение резонансное переходу 3à2 при прохождении такой среды будет усиливаться. Если усиление света превосходит его суммарное ослабление за счет поглощения в среде и потерь на частичное пропускание выходного зеркала резонатора, то возникает генерация и лазер начинает излучать свет с частотой равной частоте перехода 3à2. Очевидно, что мощность излучаемого света тем выше, чем выше мощность света накачки и чем меньше потери света внутри резонатора.
Расчет накачки. В нашем распоряжении имелась активная среда YAG-Nd3+, имеющая следующие параметры: - поперечное сечение 3х3 мм; - длина l = 30 мм и диодные матрицы с размером излучающей области 5х25 мм и пиковой мощностью излучения ~800 Вт при длительности импульса генерации 350 мкс. В этом случае удобно организовать поперечную накачку с концентрацией излучения на боковую грань активного элемента и продольную накачку с концентрацией излучения на торцевую грань активного элемента. В основе расчета накачки активной среды лежат две формулы:
и где I – интенсивность накачки (Вт/см2) при прохождении области активной среды на х (см) вглубь, I0 – интенсивность накачки (Вт/см2) в начале области, α – коэффициент поглощения (см-1), α0 – линейный коэффициент поглощения (см-1), когда I<<Is, Is – интенсивность насыщения (Вт/см2). Очевидно, что (1) и (2) – взаимосвязанные уравнения и их решение образует рекурсию по мере последовательной подстановки (1) в (2) и обратно. Физически это объясняется тем, что коэффициент поглощения уменьшается с ростом интенсивности света, а интенсивность увеличивается при уменьшении коэффициента поглощения. Такую систему удобно решать методом конечных итераций. Для этого разделим ширину прокачиваемой области кристалла на n областей (рис. 33) с шириной δ=a/n, где а – ширина кристалла.
Для расчета односторонней накачки активной среды основываемся на рассмотренном законе Бугера – Ламберта - Бера, которое записываем для последовательных шагов проводимого расчета δ и получаем следующие соотношения (3):
(3)
При введении в систему накачки второй диодной матрицы, накачивающей противоположную сторону кристалла, расчет значительно усложняется, так как появляется система из двух рекурсивных уравнений (4):
Теперь значение коэффициента поглощения α зависит не только от I1 (интенсивность излучения первой матрицы), но и от I2 (интенсивность излучения второй матрицы), которые, в свою очередь, тоже зависят от α. Из системы уравнений (4) при их сложении следует уравнение (5):
При x=0 получаем:
Для других значений x, можно получить следующие выражения, используя метод итераций с шагом δ и количеством шагов n:
Полученная формула позволяет получить значение интенсивности накачки в любой части стержня. Очевидно, что поглощенная стержнем интенсивность Ip (от англ. «pumping» – накачка) является разностью между интенсивностью, падающую на стержень и интенсивностью, выходящей из стержня после его прохождения:
Ip = b ∙(I пад - I вых), (10)
где b – количество диодных матриц (учитывая, что матрицы одинаковые и расположены симметрично относительно стержня).
I пад = k ∙ I дм, (11)
где I дм – интенсивность излучения диодной матрицы, k – коэффициент, характеризующий долю интенсивности, попадающую на стержень. Он зависит от геометрического расположения стержня в накачивающем пучке, паразитных отражений и качества полировки элементов оптической системы.
I вых = I ( n δ) - I пад , (12)
где I ( n δ) – суммарная интенсивность на боковой грани стержня. Таким образом, подставив (11), (12) в (10), получим:
Ip=b∙(2∙k∙I дм -I(n δ )), (13)
На основе представленных выражений формируем в среде MathCad цикл для проведения вычислений процесса при односторонней и двусторонней накачке алюмоиттриевого граната диодными матрицами.
|
||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

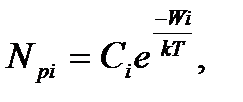 (0)
(0)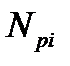 - число ионов в единице объема, находящихся на уровне i; Wi — разность между энергией уровня i и энергией основного уровня; k = 1,38∙10-23 Дж/К - постоянная Больцмана; Т - абсолютная температура кристалла, С i - нормировочная постоянная. Обычно энергию основного уровня считают условно нулевой, тогда Wi будет просто энергией i -гo уровня. [39]
- число ионов в единице объема, находящихся на уровне i; Wi — разность между энергией уровня i и энергией основного уровня; k = 1,38∙10-23 Дж/К - постоянная Больцмана; Т - абсолютная температура кристалла, С i - нормировочная постоянная. Обычно энергию основного уровня считают условно нулевой, тогда Wi будет просто энергией i -гo уровня. [39]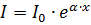 закон Бугера – Ламберта – Бера (1)
закон Бугера – Ламберта – Бера (1) 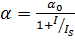 эффект насыщения поглощения (2)
эффект насыщения поглощения (2)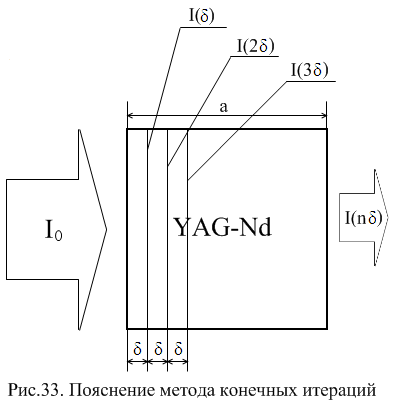
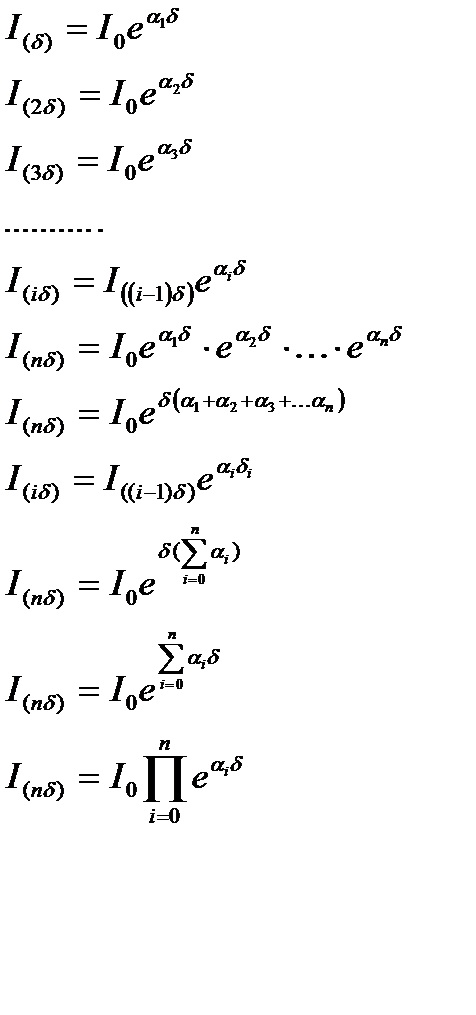
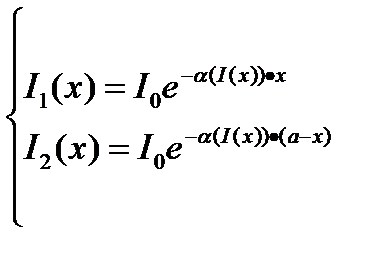 (4)
(4)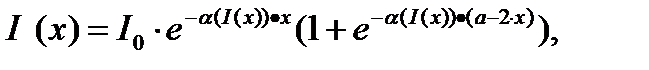 (5)
(5)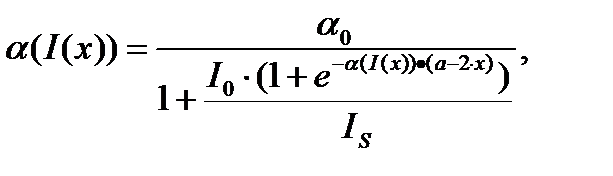 (6)
(6)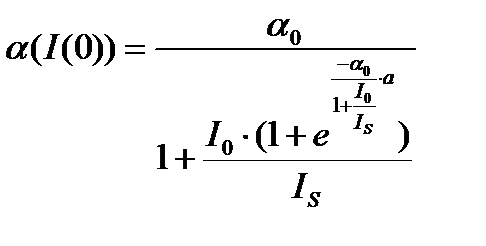 , (7)
, (7)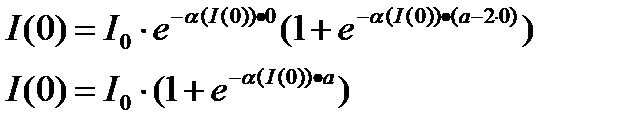 , (8)
, (8)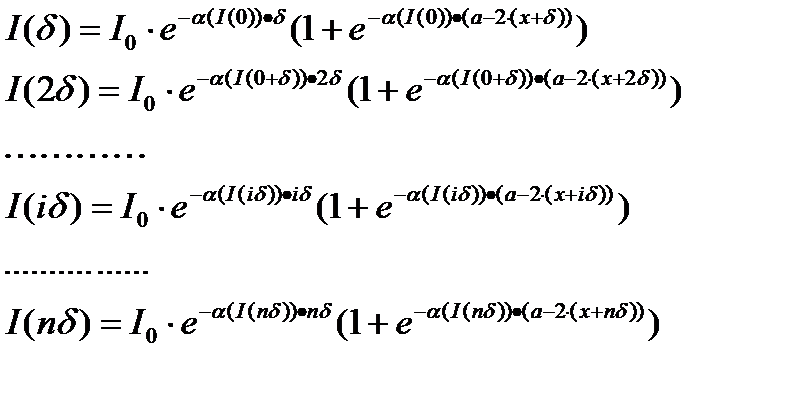 , (9)
, (9)


