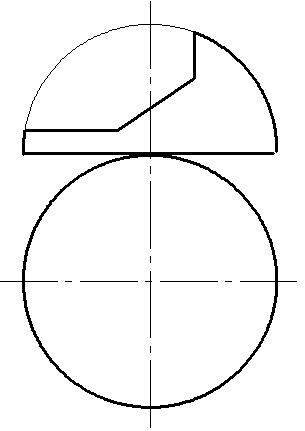Взаимное пересечение поверхностей

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ДВУХ МНОГОГРАННИКОВ

Линией пересечения двух многогранников является замкнутая ломаная линия при неполном пересечении или две замкнутые ломаные линии при полном пересечении, точками излома которых являются точки пересечения ребер одного многогранника с гранями другого, соединяемые отрезками прямых линий.

Т.е. вся задача на построение линии пересечения двух многогранников сводится к многократному решению задачи на определение точки пересечения прямой линии (ребра) с плоскостью (гранью).

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА С КРИВОЙ ПОВЕРХНОСТЬЮ

Линия пересечения многогранника с кривой поверхностью представляет собой замкнутую ломаную линию при неполном пересечении или две замкнутые ломаные линии при полном пересечении, точками излома которых являются точки пересечения ребер многогранника с кривой поверхностью, соединяемых дугами кривых или прямых линий в зависимости от взаимного положения кривой поверхности и грани многогранника.

Задача на построение линии пересечения многогранника с кривой поверхностью сводится к многократному решению двух задач:

• Построение точек пересечения ребер многогранника с кривой поверхностью (пересечение прямой линии с поверхностью).
• Построение линии пересечения грани многогранника с кривой поверхностью (пересечение поверхности плоскостью).

 

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ДВУХ КРИВЫХ ПОВЕРХНОСТЕЙ

Линией пересечения двух кривых поверхностей является одна или две пространственные (возможны и плоские) кривые при полном или неполном пересечении соответственно.

Для получения таких линий должны быть введены вспомогательные секущие поверхности-посредники как плоские, так и кривые.

Обязательные требования, предъявляемые к секущим поверхностям-посредникам:

• каждая из секущих поверхностей-посредников должна пересекать обе заданные поверхности;

• линии, получаемые в результате пересечения должны иметь наиболее простую геометрическую форму и попарно пересекаться между собой.

                                      

Общий алгоритм построения

     Φ ∩ Ω = l { K ¹, K ², K ³,… K ⁱ}

     S ⁱ - секущая поверхность-посредник

     S ⁱ ∩ Φ = m ⁱ; S ⁱ ∩ Ω = n ⁱ

              m ⁱ ∩ n ⁱ = К ⁱ

 

             

               

 

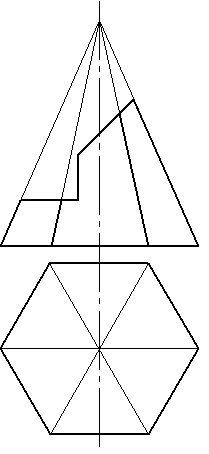
4.7 Достроить горизонтальную и построить профильную проекцию пирамиды, имеющей призматический вырез

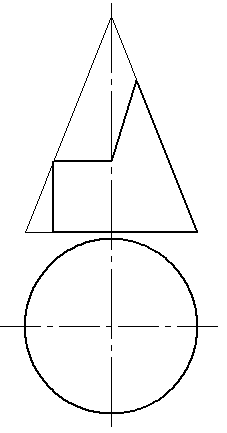
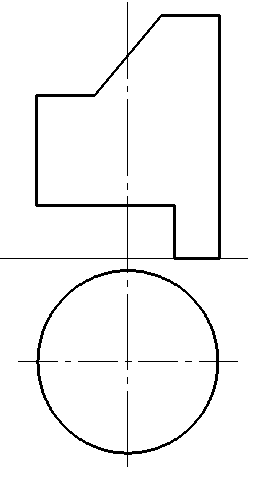
4.8 Достроить горизонтальную и построить профильную проекции конуса и цилиндра, имеющих призматический вырез

 

4.9 Достроить горизонтальную и построить профильную проекцию половины сферы имеющей сложный вырез.

 

Аксонометрические проекции

Аксонометрическая проекция – это наглядное изображение объекта, представляющее собой проекцию на одну плоскость объекта, отнесенного в пространстве к системе координат 0 xyz.

ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ

s – направление проецирования;

П ¢ – плоскость проекций (картина);

O ¢ x ¢, O ¢ y ¢, O ¢ z ¢ – аксонометрические оси координат;

Точка А ¢ xy – вторичная проекция точки А;

  Ð φ = s ^ П ¢ – угол между направлением проецирования и плоскостью проекций.

В зависимости от выбранного направления проецированияпараллельные аксонометрические проекции подразделяются на:

• прямоугольные (Ðφ = 90º)

• косоугольные (Ðφ ≠ 90º)