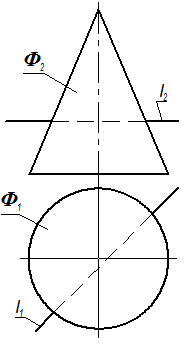Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
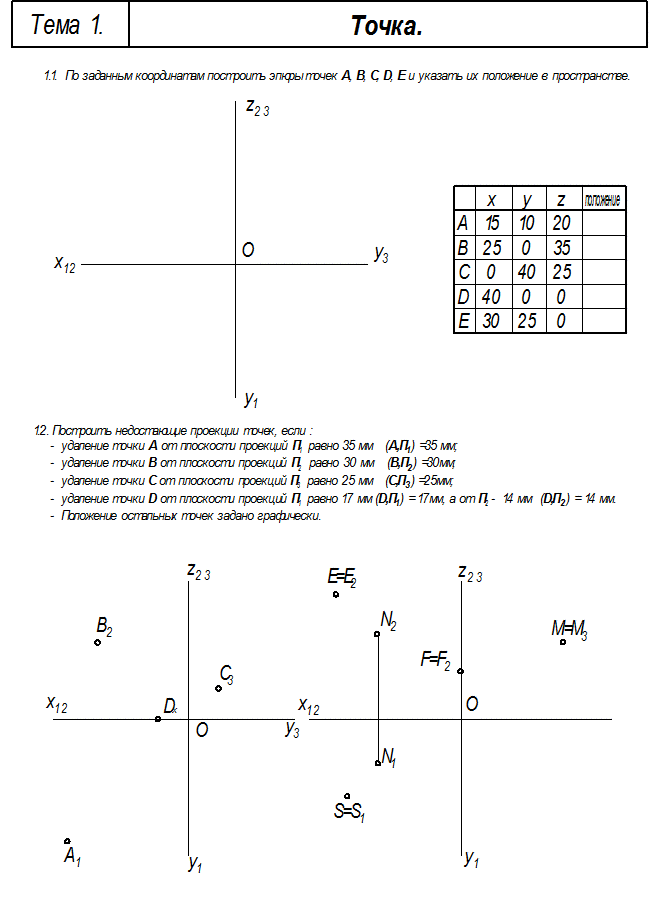
Символы, обозначающие отношения между геометрическими фигурамиСтр 1 из 7Следующая ⇒
Обозначения 1. Точки обозначают прописными буквами латинского алфавита или арабскими цифрам: A, B, C, D, …. 1, 2, 3, 4, …. 2. Линии, произвольно расположенные по отношению к плоскости проекций, обозначают строчными буквами латинского алфавита: a, b, c, d, …. Линии уровня обозначают: h - горизонталь, f - фронталь, p - профильная прямая. Для прямых используют также следующие обозначения: (АВ) - прямая, проходящая через точки А и В; IABI - длина отрезка АВ (расстояние между точками А и В). 3. Поверхности (плоскости) обозначают прописными буквами греческого алфавита (кроме буквы П): для кривых поверхностей - Ω, Φ, … для плоскостей - Γ, Δ, Λ, Τ,… 4. Углы обозначают строчными греческими буквами: α, β, γ, δ, φ, ψ,… 5. Прямой угол на эпюре отмечают дугой с точкой внутри сектора. 6. Плоскости проекций обозначают прописными буквами П (пи) греческого алфавита с добавлением подстрочного индекса: Основные: П1 - горизонтальная плоскость проекций, П2 - фронтальная плоскость проекций, П3 - профильная плоскость проекций Дополнительные: П4, П5, П6, … Для аксонометрических проекций: Пк. 7. Проекции точек, линий, произвольных поверхностей (плоскостей), поверхностей геометрических фигур обозначают теми же буквами (цифрами), что и оригинал, но с добавлением подстрочного индекса соответствующей плоскости проекций, на которой они получены: горизонтальные проекции: А1,В1,С1,…11,21,31,…a1,b1,c1,…Φ1,Ω1,…Δ1,Λ1,Σ1 … фронтальные проекции: А2,В2,С2,…12,22,32,…a2,b2,c2,…Φ2,Ω2,…Δ2,Λ2,Σ2 … профильные проекции: А3,В3,С3,…13,23,33,…a3,b3,c3,…Φ3,Ω3,…Δ3,Λ3,Σ3 … Символы, обозначающие отношения между геометрическими фигурами
Обозначения теоретико-множественные
БАЗОВЫЕ ГЕОМЕТРИЧЕСКИЕ ЭЛЕМЕНТЫ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Точка – абстрактное математическое понятие. Нульмерный объект (не имеет измерений).
Линия - непрерывное одномерное множество точек (цепочка точек). Измерение: только длина. Толщины нет.
Поверхность – непрерывное двумерное множество точек. Измерения: длина, ширина, площадь. Толщины и объема нет.
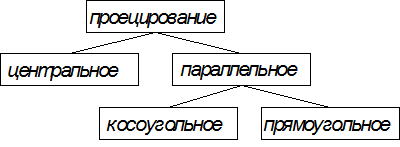
Метод проецирования
Все изображения, построенные на основе метода проецирования, называются проекционными. ВАРИАНТЫ МЕТОДА ПРОЕЦИРОВАНИЯ
ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ПРОЕКЦИОННОМУ ИЗОБРАЖЕНИЮ
1. Наглядность - свойство, которое дает возможность по изображению представить внешнюю форму заданного объекта. 2. Обратимость - свойство, на основе которого по изображению можно восстановить реальную форму объекта, его размеры и, если необходимо, положение заданного объекта в пространстве. 3. ЕДИНСТВО ПРАВИЛ построения изображения и правил его графического оформления.
Перспективная проекция Аксонометрическая проекция Ортогональные проекции Выводы • Выбор того или иного вида проекции определяется функциональным назначением получаемого изображения. • Для презентаций определяющим свойством является наглядность изображения (перспективная или аксонометрическая проекция). • Для разработки технологического процесса изготовления (строительства) объекта определяющим свойством является обратимость изображения (ортогональные проекции).
СВОЙСТВА ПРОЕЦИРОВАНИЯ Общие свойства
Инвариантные свойства параллельного проецирования
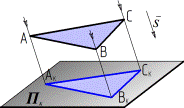
1. Если отрезок прямой делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией точки в том же отношении 2. Если прямые в пространстве параллельны, то их одноименные проекции также параллельны. (m 2 n) Þ (mk 2 nk). 3. Eсли плоская фигура параллельна плоскости проекций, то ее проекция на этой плоскости конгруэнтна самой фигуре. (Ф (АВС) 2 Пk) Þ (Фк (АкВкСк) @ Ф (АВС))
Получение обратимых изображений
Метод Монжа Точка в первом октанте
Условия, которым должен удовлетворять эпюр точки, расположенной в любой части пространства, в системе трех ортогональных плоскостей проекций: • А1А2 ^ Х1,2 ______________________________________________________________ • А2А3 ^ Z2,3 ______________________________________________________________ • (A1,Х1,2) = (A3,Z2,3) ________________________________________________________ _______________________________________________________________________________
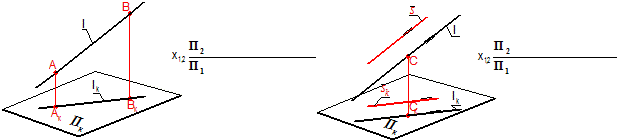
Прямая линия Способы задания прямой на эпюре
Через две точки Через точку параллельно заданному направлению Прямая общего положения
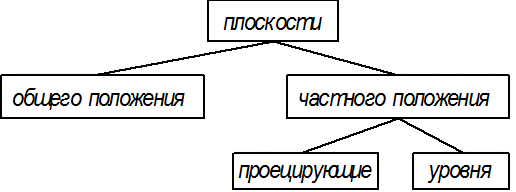
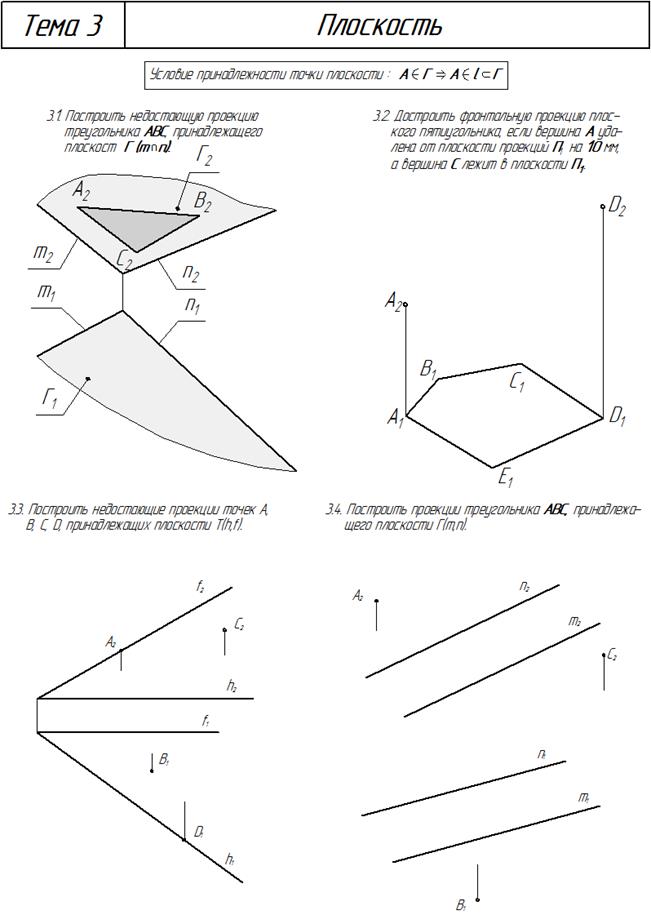
Прямые частного положения Плоскость П лоскость – плоская поверхность. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ
Т(А, В, С) S(А, b) D(a Ç b) W(m 2 n) F(ABC) Изображение плоскости на эпюре
Положение плоскости относительно плоскостей проекций
Плоскости общего положения - это плоскости не параллельные и не перпендикулярные плоскостям проекций. Вывод: Ни одна из проекций плоскости общего положения не имеет форму прямой линии (см. способы задания и изображение плоскостей).
Плоскости частного положения Проецирующие плоскости – это плоскости перпендикулярные одной из плоскостей проекций. Горизонтально проецирующая плоскость -________________________________________ Фронтально проецирующая плоскость -____________________________________________ Плоскости уровня – этоплоскости параллельные одной из плоскостей проекций. Горизонтальная плоскость уровня - _______________________________________________ Фронтальная плоскость уровня -__________________________________________________ Вывод: У плоскости частного положения одна из проекций обязательно имеет форму прямой линии. Прямая линия и плоскость Прямые в плоскости Прямая принадлежит плоскости, если две точки прямой принадлежат этой плоскости l (1,2)Ì Т Þ (1 Î m; m Ì T) Ù(2 Î n; n Ì T) или одна точка прямой принадлежит плоскости и она параллельна прямой лежащей в плоскости. l (А, d)Ì Т Þ (А ÎT;) Ù(l II d; d Ì T) В качестве примера плоскость Т задаем треугольником АВС. Требуется построить произвольную прямую l, принадлежащую плоскости Т. Первый вариант Второй вариант
ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ К главным линиям плоскости относятся прямые уровня - горизонталь, фронталь, профильная прямая, и линии наибольшего наклона плоскости. Прямые уровня плоскости 1) Горизонталь плоскости – прямая, принадлежащая плоскости, и параллельная горизонтальной плоскости проекций. 2) Фронталь плоскости – прямая, принадлежащая плоскости, и параллельная фронтальной плоскости проекций.
Точка на плоскости
Точка принадлежит плоскости, если она принадлежит прямой, принадлежащей этой плоскости. А Î Т Þ А Î l; l Ì T Построить проекции произвольной точки А, принадлежащей плоскости Т (m, n) Первый вариант Второй вариант
АÎ l; l(1, 2)Ì T; задаем (1Îm); (2În) AÎl; l(1, S) задаем (1În), (l||m) Взаимное положение двух плоскостей Параллельные плоскости
Через точку А провести плоскость Р параллельную плоскости Т.
T(aÇb); P(cÇd); провести: c || a Ù d || b Þ T || P
Пересекающиеся плоскости Частный случай: одна из двух пересекающихся – плоскостей плоскость частного положения. Т – фронтально-проецирующая плоскость. Р (D АВС) – плоскость общего положения
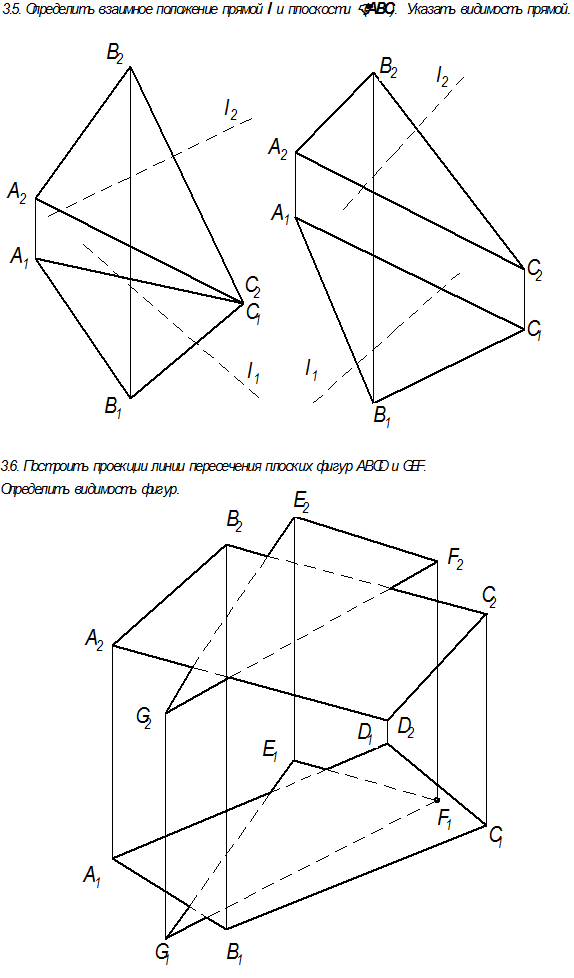
Взаимное положение прямой линии и плоскости Прямая по отношению к плоскости может занимать следующие положения:
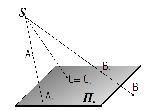
Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости. l ‖Ф Û l ‖ m; m ÌФ
l ∩Ф Û l ∩ m; m ÌФ
l ÌФ Û l ≡ m; m ÌФ
Так как во всех представленных вариантах определения взаимного положения прямой и плоскости прямая рассматривается не по отношению к самой плоскости, а по отношению какой-то прямой, принадлежащей этой плоскости, то необходимо сформулировать способ нахождения такой дополнительной прямой. Параллельность, пересечение и совпадение (тождественность) двух прямых возможно только при условии, что обе прямые лежат в одной общей плоскости.
Поверхности
Поверхность – это непрерывное множество последовательных положений линии, перемещающейся в пространстве по определенному закону g - образующая поверхности d - направляющая поверхности
Если образующая является прямой, то поверхность линейчатая Если образующая является кривой, то поверхность не линейчатая
ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ Образующая поверхности – прямая линия С одной направляющей и вершиной (S) - ТОРСОВЫЕ поверхности
Направляющая имеет форму кривой линии:
Направляющая имеет форму прямой линии. Поверхность плоская – ПЛОСКОСТЬ
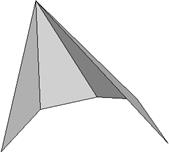
Направляющая имеет форму ломаной линии. ГРАННЫЕ поверхности. Каждая грань – это ПЛОСКОСТЬ Линии пересечения граней – это РЕБРО Точки пересечения ребер – это ВЕРШИНА
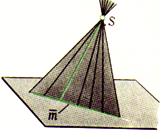
S- реальная точка. Ф{g(d,S)(g∩d, SÎ g)}- ПИРАМИДАЛЬНАЯ поверхность
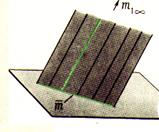
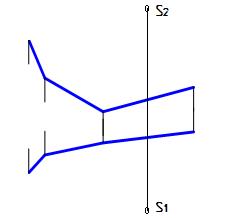
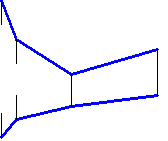
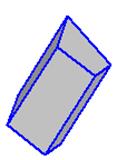
S - несобственная точка Þ s – направление проецирования. Ф{g(d,s)(g∩d, gIIs)}– ПРИЗМАТИЧЕСКАЯ поверхность
ПОВЕРХНОСТИ ВРАЩЕНИЯ
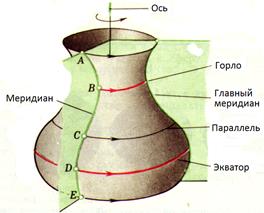
Основные элементы поверхности вращения
Поверхность вращения можно рассматривать как непрерывное множество точек, принадлежащих образующей при её вращении вокруг оси. НЕ ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ
Тор открытый Тор закрытый Сфера Глобоид
R < t - открытый тор R > t – закрытый тор t = 0 – сфера
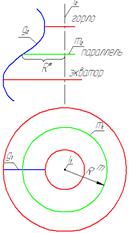
Линейчатая поверхность. На линейчатой поверхности вращения линия l, которой должна принадлежать точка, может иметь форму как прямой линии (образующая), так и окружности (параллель) Нелинейчатая поверхность. На нелинейчатой поверхности вращения линия l, которой должна принадлежать точка, должна иметь форму только окружности (параллели).
Пересечение поверхности плоскостью Форма линии пересечения поверхности плоскостью определяется формой заданной поверхности и положением плоскости относительно этой поверхности. Для кривой поверхности, в общем случае, линия пересечения - это плоская кривая линия. ПЕРЕСЕЧЕНИЕ ГРАННОЙ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
При пересечении гранной поверхности плоскостью линия пересечения – это ломаная линия, каждый участок которой – отрезок прямой, представляющий собой линию пересечения грани поверхности (отсека плоскости) с секущей плоскостью, а точки излома – точки пересечения ребер гранной поверхности (отрезков прямых) с той же секущей плоскостью. Следовательно, решение задачи на построение линии пересечения сводится к определению точек пересечения ребер гранной поверхности с принятой секущей плоскостью.
ПЕРЕСЕЧЕНИЕ КОНИЧЕСКОЙ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
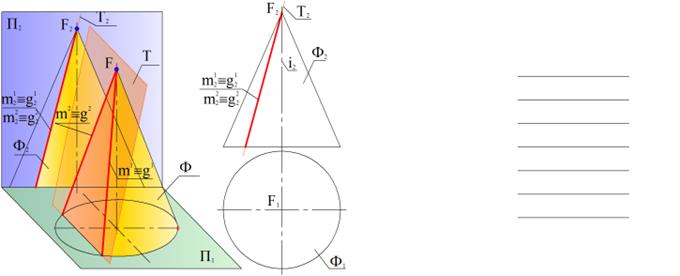
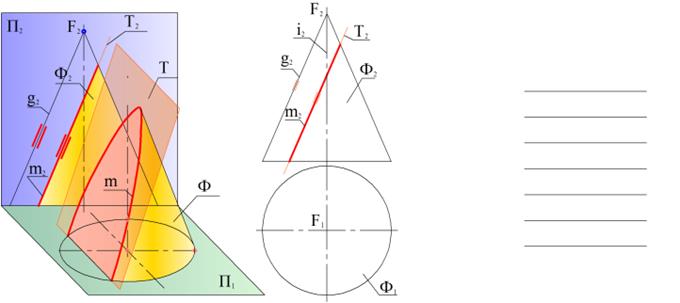
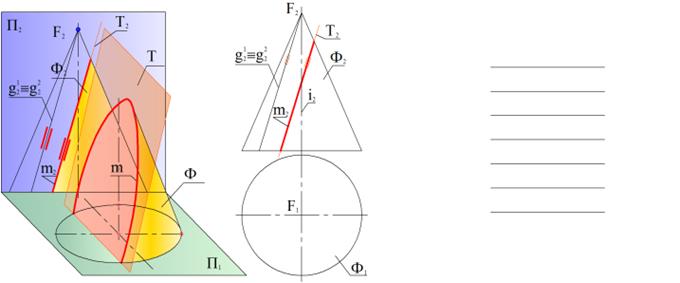
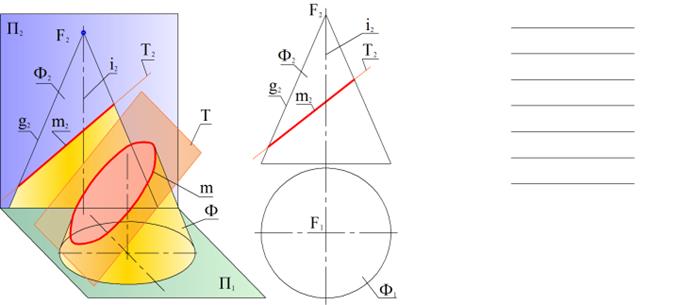
Форма линии пересечения прямой круговой конической поверхности плоскостью определяется положением секущей плоскости относительно отдельных элементов поверхности. Ф – прямая круговая коническая поверхность. Т – секущая плоскость. Ф ∩ Т = m – линия пересечения.
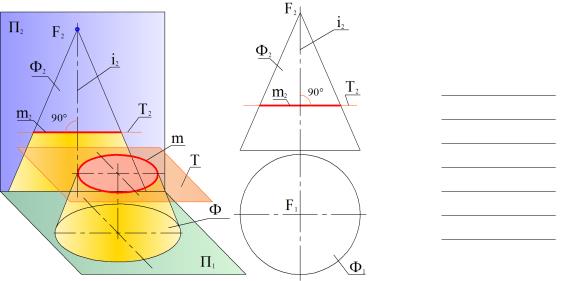
В общем случае решение задачи на построение линии пересечения конической поверхности плоскостью сводится к определению точек пересечения образующих поверхности с принятой секущей плоскостью. Положение точек на поверхности конуса определяется через образующие g(FA, FB) или по параллелям m (R). Радиус (R) параллели изменяется в зависимости от высоты положения точки на поверхности конуса (чем выше, тем меньше). ПЕРЕСЕЧЕНИЕ ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
Форма линии пересечения прямой круговой цилиндрической поверхности плоскостью определяется положением секущей плоскости относительно отдельных элементов поверхности. Ф – прямая круговая цилиндрическая поверхность; Т – секущая плоскость; Ф ∩ Т = m – линия пересечения.
ПЕРЕСЕЧЕНИЕ ШАРА ПЛОСКОСТЬЮ При пересечении сферической поверхности плоскостью фигура сечения всегда имеет форму окружности. На проекциях фигура сечения может иметь форму окружности, эллипса или прямой линии, в зависимости от положения секущей плоскости по отношению к той плоскости проекций, на которой строится проекция фигуры сечения. Окружность, по которой плоскость пересечет сферу, проецируется на П1 в виде эллипса. Для построения сечения используются не образующие, а параллели и меридианы. Две точки этого эллипса 1 и 2 – на главном меридиане. Точки 3 и 4 – на экваторе (они определяют видимость горизонтальной проекции сечения). Точки 5 и 6 определяют положение большой оси эллипса, длина которой равна диаметру окружности сечения, т.е. отрезок 51-61 равен отрезку 12-22. Остальные точки эллипса находятся на параллелях и берутся произвольно. Например, точки 7 и 8. Определим на фронтальной проекции радиус окружности параллели и построив её на горизонтальной плоскости проекций.
Пересечение прямой линии с поверхностью
l ∩ Φ ═ { K 1, K 2,… }; { K 1, K 2,… }= l ∩ m; m Ì Φ Последовательность действий при построении точек пересечения прямой с поверхностью аналогична действиям, выполняемым при построении точки пересечения прямой линии с плоскостью, так как плоскость является одной из разновидностей поверхности.
Последовательность действий при построении точек пересечения прямой линии с поверхностью 1. Определить вид заданной поверхности для выявления возможных простых форм сечений плоскостью (ломаная линия или окружность), и установить при каком положении секущей плоскости эти простые формы сечений могут быть получены. 2. Прямую l заключить в выбранную секущую плоскость, например, Т. l È Т Наиболее часто применяют проецирующие плоскости. Для этого на эпюре нужно одну из проекций прямой l совместить с одноименной проекцией плоскости Т. Т ^ П к Þ l кº Т к
Т ∩ Ф = m { 1,2,3,… }
l ∩ m = { K1, K2,… }
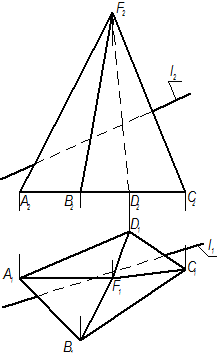
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ГРАННОЙ ПОВЕРХНОСТЬЮ
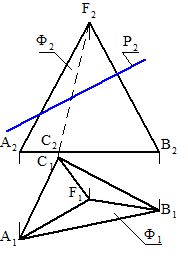
FABCD – четырехгранная пирамида. Определить точки К 1 и К 2 пересечения прямой l с поверхностью пирамиды. l ∩ Φ(FABCD) = { К 1, К 2} Заданная поверхность является гранной. При пересечении такой поверхности любой плоскостью фигурой сечения всегда будет многоугольник (ломаная линия). Поэтому применяем проецирующую вспомогательную секущую плоскость. Заключаем прямую во фронтально-проецирующую плоскость. Строим горизонтальную проекцию m1, при условии, что m Ì Φ (FABCD); m {1,2,3,4}; 1 = FA ∩ T; 2= FB ∩ T; 3= FC ∩ T; 4= FD ∩ T. Определяем точки К11 и К21 пересечения линии m1 с l1. m1 ∩ l1 ={ K11, К21}Строим фронтальные проекции К12 и К22 точек К1 и К2. Определяем видимость участков прямой l. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С КОНИЧЕСКОЙ ПОВЕРХНОСТЬЮ
Задан прямой круговой конус. Определить точки К1 и К2 пересечения прямой l с поверхностью конуса. l ∩ Φ = { К 1, К 2}
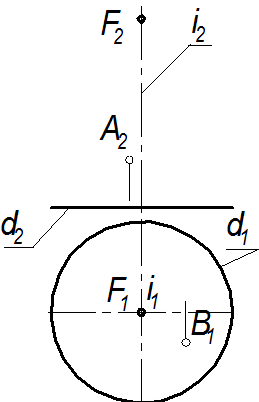
У круговой конической поверхности есть две простые формы сечения плоскостью – две прямые (образующие) и окружность. Заданная прямая – горизонталь. Следовательно, заключив прямую l в горизонтальную секущую плоскость перпендикулярную оси вращения конической поверхности, получим сечение в форме окружности. Заключаем прямую lв горизонтальную плоскость уровня Т. Строим проекции горизонтальную проекцию сечения. Определяем точки пересечения сечения с прямой l. Определяем видимость участков прямой l.
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ С КОНУСОМ.
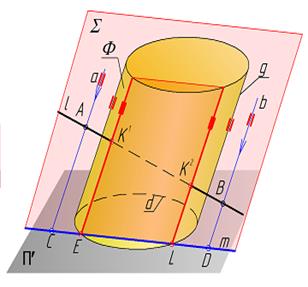
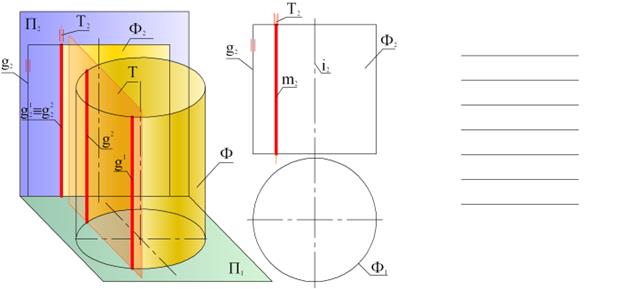
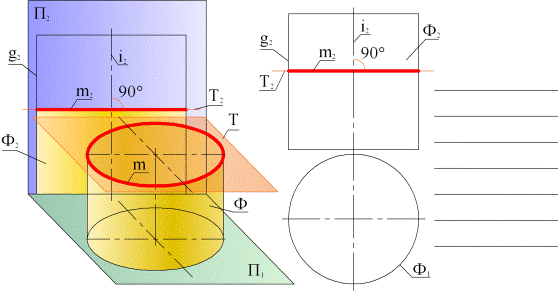
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТЬЮ 1.Заключить прямую l в секущую плоскость, идущую вдоль образующих цилиндра. l È S(l Ç а \\ g); прямая «a» проходит вдоль образующих цилиндра и пересекает прямую «l» в точке А.l È S(l Ç b \\ g) – «b» пересекает «l» в точка В. 2. с = S ÇФ – для построения сечения «с» определить положение горизонтальных следов прямых, образующих секущую плоскость (точки С и D). Прямая «m» пересекает основание цилиндра в точках Е, L. Построить сечение. 3. К1,К2 = l Ç с – определить точки пересечения прямой с цилиндром. Точки наложения прямой на сечение. 4. Показать видимость прямой относительно поверхности цилиндра.
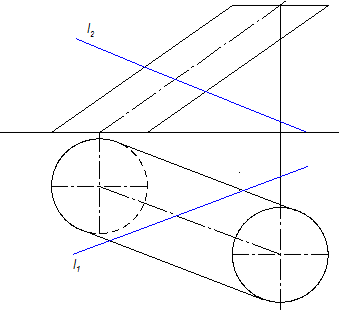
ПЕРЕСЕЧЕНИЕ ТОРА С ПРЯМОЙ ЛИНИЕЙ.
Аксонометрические проекции Аксонометрическая проекция – это наглядное изображение объекта, представляющее собой проекцию на одну плоскость объекта, отнесенного в пространстве к системе координат 0 xyz. ПАРАЛЛЕЛЬНАЯ АКСОНОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ
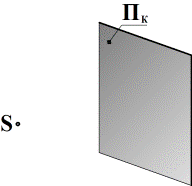
s – направление проецирования; П ¢ – плоскость проекций (картина); O ¢ x ¢, O ¢ y ¢, O ¢ z ¢ – аксонометрические оси координат; Точка А ¢ xy – вторичная проекция точки А; Ð φ = s ^ П ¢ – угол между направлением проецирования и плоскостью проекций. В зависимости от выбранного направления проецированияпараллельные аксонометрические проекции подразделяются на: • прямоугольные (Ðφ = 90º) • косоугольные (Ðφ ≠ 90º) О Г Л А В Л Е Н И Е
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.205.223 (0.258 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
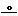


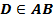




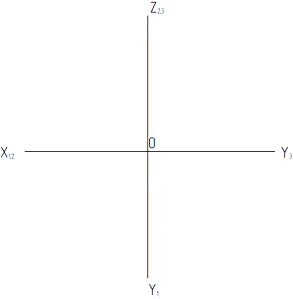


 ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
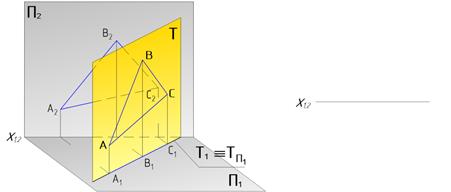
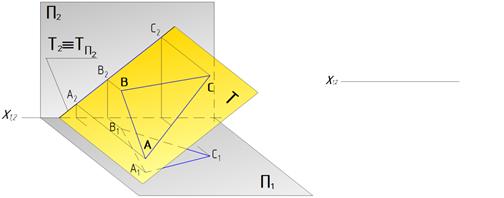
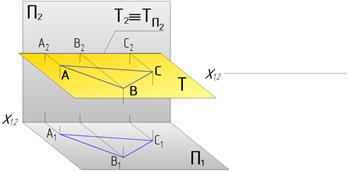
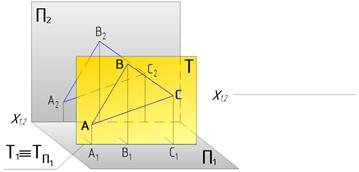
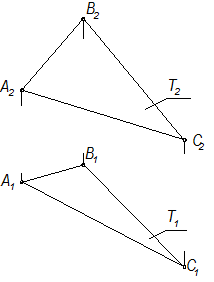

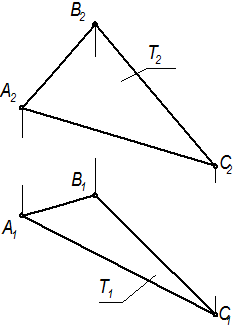
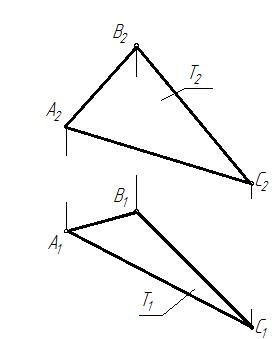

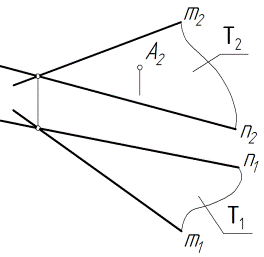
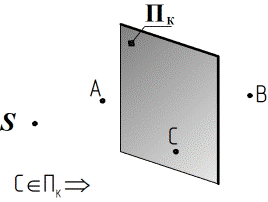
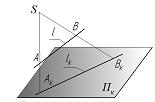
 Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.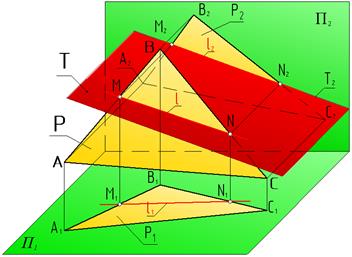


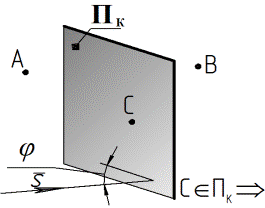
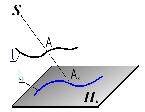
 Прямая пересекает плоскость, если она пересекает какую-либо прямую, принадлежащую этой плоскости.
Прямая пересекает плоскость, если она пересекает какую-либо прямую, принадлежащую этой плоскости. Прямая принадлежит плоскости, если она тождественна какой-либо прямой, принадлежащей этой плоскости.
Прямая принадлежит плоскости, если она тождественна какой-либо прямой, принадлежащей этой плоскости. 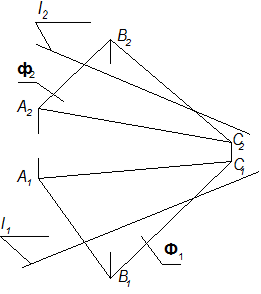


 В качестве основного метода формирования поверхности принят кинематический.
В качестве основного метода формирования поверхности принят кинематический.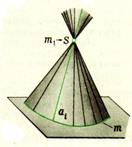 S- реальная точка
S- реальная точка
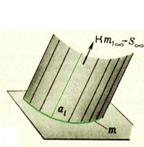 S - несобственная точка Þ
s – направление проецирования
S - несобственная точка Þ
s – направление проецирования






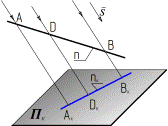
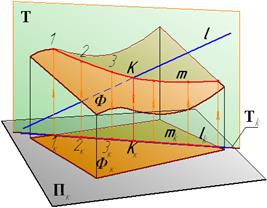 Прямая пересекает поверхность, если она пересекает какую-либо линию, принадлежащую этой поверхности
Прямая пересекает поверхность, если она пересекает какую-либо линию, принадлежащую этой поверхности