
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторное произведение векторов ⇐ ПредыдущаяСтр 8 из 8
Определение. Упорядоченнаятройка некомпланарных векторов называется «правой», если кратчайший поворот от вектора
Тройка правая Тройка левая
Происхождение названия: если векторы Смысл декартовой тройки Определение. Векторным произведением векторов 1) Обозначение Геометрический смысл векторного произведения
Тогда площадь треугольника Механический смысл векторного произведения 1)
 
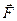 приложена к точке В. Тогда моментом силы приложена к точке В. Тогда моментом силы  относительно точки А называется вектор относительно точки А называется вектор  такой, что такой, что 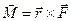 , где вектор , где вектор  - плечо АВ, - плечо АВ,  . .
2) Пусть материальная точка движется по окружности с центром в точке О,
  - линейная скорость движения точки, - линейная скорость движения точки,  - радиус-вектор точки М. Тогда угловой скоростью материальной точки называется вектор - радиус-вектор точки М. Тогда угловой скоростью материальной точки называется вектор  такой, что такой, что  . . 
Свойства векторного произведения. 1. Частный случай: 2. 3. Если (Пояснение: если одну из сторон параллелограмма увеличить в λ раз, не меняя ее направление, то и площадь увеличиться в λ раз). 4.
Таблица векторного умножения ортов
Векторное произведение векторов, заданных своими декартовыми координатами Два вектора Найдем векторное произведение данных векторов, перемножая их как многочлены (согласно свойств векторного произведения):
Выражения в скобках получаются при вычислении определителей 2-го порядка, поэтому можно записать: формула для нахождения векторного произведения векторов, заданных своими декартовыми координатами. Можем записать, что координаты вектора векторного произведения равны:
Примеры. Пример 1. Векторы Решение.
Пример 2. Даны Решение. Из свойства Из основного тригонометрического тождества следует, что Найдем Пример 3. Векторы Решение.
= Пример 4. Даны два вектора Решение. Найдем координаты векторов
Пример 5. Сила Решение. Найдем вектор
Пример 6. Даны три вершины параллелограмма ABCD: А (2, -1, 2), В (1, 2, -1), С (3, 2, 1). Найти его площадь. Решение. Найдем векторы, на которых построен параллелограмм:
§ 4. Смешанное произведение векторов Определение. Смешанным произведением трех векторов называется число, равное
 
 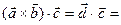 по определению = по определению =  пр пр  . .
 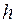 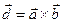 , где , где  - площадь параллелограмма, построенного - площадь параллелограмма, построенного
на векторах Свойства смешанного произведения. 1. При циклической перестановке множителей смешанное произведение не изменяется. Данное свойство позволяет ввести новое обозначение смешанного произведения: 2. Условие компланарности трех векторов:
Т.е. параллелепипед вырождается в часть плоскости с нулевым объемом. 3.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 73; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.15.248 (0.034 с.) |
 к вектору
к вектору  , когда смотрим с конца вектора
, когда смотрим с конца вектора  , происходит против часовой стрелки. Если же этот поворот кажется происходящим по часовой стрелке, то тройка векторов называется «левой».
, происходит против часовой стрелки. Если же этот поворот кажется происходящим по часовой стрелке, то тройка векторов называется «левой».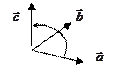
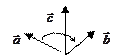
 совпадают соответственно с большим, указательным и средним пальцами правой руки – тройка правая, если левой руки – тройка левая.
совпадают соответственно с большим, указательным и средним пальцами правой руки – тройка правая, если левой руки – тройка левая.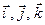 всегда должен соответствовать правилу винта: правый винт (раскручиваем вправо, вкручиваем влево)) – тройка правая, левый винт – тройка левая.
всегда должен соответствовать правилу винта: правый винт (раскручиваем вправо, вкручиваем влево)) – тройка правая, левый винт – тройка левая.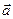 и
и  называется вектор
называется вектор 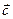 , удовлетворяющий условиям:
, удовлетворяющий условиям: , 2)
, 2) 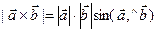 , 3)
, 3)  образуют правую тройку. (1)
образуют правую тройку. (1) или
или  .
. 
 Модуль векторного произведения
Модуль векторного произведения  равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах  и
и  .
.  . (2)
. (2) 
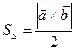 .
.



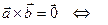
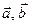 – коллинеарные векторы. (3)
– коллинеарные векторы. (3)
 (Пояснение: из-за смены троек) (антиперестановочное)
(Пояснение: из-за смены троек) (антиперестановочное) – действительное число, то
– действительное число, то 
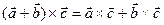 ,
,  Перемножаем, строго соблюдая порядок.
Перемножаем, строго соблюдая порядок.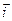
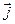


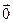



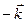




 и
и 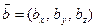 заданы своими декартовыми координатами. Разложим их по ортам
заданы своими декартовыми координатами. Разложим их по ортам  :
:  ,
, 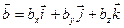 .
.


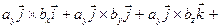
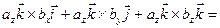 =
= 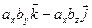

 =
= 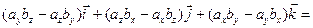
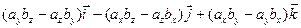 .
. – разложение по первой строке определителя 3-го порядка:
– разложение по первой строке определителя 3-го порядка: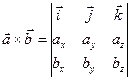 – (4)
– (4)  .
. и
и 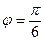 . Зная
. Зная 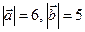 , вычислить
, вычислить  .
. =
=  . Ответ: 15.
. Ответ: 15. ,
, 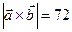 . Вычислить скалярное произведение векторов
. Вычислить скалярное произведение векторов 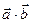 .
.  .
.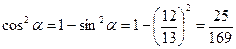 .
. :
:  . По определению найдем скалярное произведение векторов:
. По определению найдем скалярное произведение векторов:  =
= 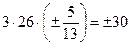
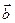 образуют угол
образуют угол 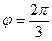 . Зная
. Зная 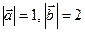 , вычислить
, вычислить  .
. 

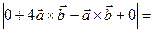
 3
3 
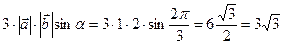 .
.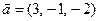 и
и 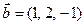 . Найти координаты векторного произведения векторов
. Найти координаты векторного произведения векторов 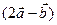 и
и 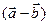 .
. 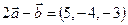 ,
,  .
.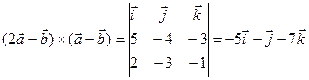 . Ответ:
. Ответ: 
 приложена к точке В (4, -2, 3). Определить момент этой силы относительно точки А (3, 2, -1) и его величину.
приложена к точке В (4, -2, 3). Определить момент этой силы относительно точки А (3, 2, -1) и его величину.  .
.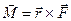 =
= 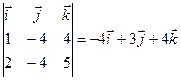 .
.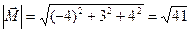 . Ответ:
. Ответ: 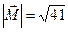
 ,
,  (векторы должны выходить из одной точки).
(векторы должны выходить из одной точки).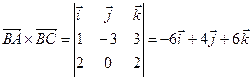 . Тогда
. Тогда  ед.кв..
ед.кв.. , обозначается
, обозначается 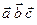 .
.



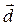









 . Вектор
. Вектор 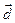 поопределению векторного произведенияперпендикулярен векторам
поопределению векторного произведенияперпендикулярен векторам  , следовательно, перпендикулярен плоскости параллелограмма. Построим на векторах
, следовательно, перпендикулярен плоскости параллелограмма. Построим на векторах 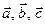 параллелепипед. Тогда пр
параллелепипед. Тогда пр 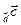 = h – это высота данного параллелепипеда для правой тройки векторов, пр
= h – это высота данного параллелепипеда для правой тройки векторов, пр  – для левой. Отсюда, т.е.
– для левой. Отсюда, т.е.  , где V – объем параллелепипеда, построенного на векторах
, где V – объем параллелепипеда, построенного на векторах  . Итак,
. Итак,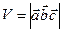 . (1)
. (1)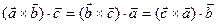 .
. , так как результат не зависит, как расставляются скобки.
, так как результат не зависит, как расставляются скобки.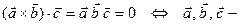 компланарные векторы. (2)
компланарные векторы. (2)
 образуют базис во множестве векторов. (3)
образуют базис во множестве векторов. (3)


