Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П. 2. Действия над матрицамиСтр 1 из 8Следующая ⇒
Матрицы П. 1. Основные определения Определение 1. Матрицей размера m Обозначают матрицу так:
Числа Например, матрица размерности Определение 2. Матрица называется квадратной порядка n, если m = n, и прямоугольной размерности m на n, если m В квадратной матрице
элементы Определение 3. Две матрицы называются равными, если их размеры совпадают и соответствующие элементы равны.
Определение 4. Транспонированной матрицей к матрице Например, Определение 5. Квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной.
Определение 6. Диагональная матрица, у которой элементы главной диагонали единицы, называется единичной, обозначается буквой Е: Определение 7. Квадратная матрица называется треугольной, лежащие по одну сторону одной из ее главных диагоналей – нули.
Определение 8. Матрица, состоящая из одной строки, называется матрицей-строкой. Матрица, состоящая из одного столбца, называется матрицей-столбцом:
Определение 9. Матрица, все элементы которой равны 0, называется 0-матрицей (нуль-матрицей) и обозначается буквой О
Определители Определение 12. Определителем (детерминантом) квадратной матрицы А называется число, которое обозначается символом
Правила вычисления определителей 1. Определитель квадратной матрицы порядка n = 1:
2. Определитель квадратной матрицы порядка n = 2:
Пример. 3. Определитель квадратной матрицы порядка n = 3:
(+) (-)
Пример.
4. Определитель квадратной матрицы порядка n вычисляется либо разложением по строке или столбцу (методом понижения порядка), либо методом приведения к треугольному виду. Рассмотрим вычисление определителя разложением по строке или столбцу (методом понижения порядка). Прежде, чем его рассмотреть, отметим ряд свойств определителя и дадим несколько определений. Свойства определителя 1. Определитель не изменяется при транспонировании.
2. При перестановке двух строк (столбцов) определитель меняет знак.
3. Если две строки (столбца) определителя совпадают, то он равен нулю.
4. Если все элементы какой-нибудь строки (столбца) определителя имеют общий множитель, то его можно вынести за знак определителя.
5. Если все элементы какой-нибудь строки (столбца) определителя есть нули, то det А = 0.
6. Если элементы двух строк (столбцов) взаимно пропорциональны, то det А = 0. 7. Если каждый элемент некоторой строки определителя представляет собой сумму двух слагаемых, то определитель представляется в виде суммы двух определителей, у которых элементы рассматриваемой строки в первом определителе равны первым слагаемым, во втором – вторым. (Аналогично со столбцами). Например,
8. Определитель не изменится, если к элементам одной строки (столбца) прибавить другую строку (столбец), умноженную на действительное число. Например, умножим первую строку на 2 и сложим с соответствующими элементами второй строки, результат поставим на место второй строки, а первую оставим без изменения:
9. Определитель треугольной матрицы равен произведению элементов, стоящих на ее главной диагонали.
Определение 13. Минором элемента
Определение 14. Алгебраическим дополнением элемента Пример. Найти Решение. Вычеркнем в определителе вторую строку и третий столбец, тогда минор
Понятие о ранге матрицы.
Пусть дана матрица А размером
Выберем произвольно в этой матрице k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу k -го порядка
Определение 17. Наивысший порядок отличных от нуля миноров называется рангом матрицы. Обозначается ранг матрицы Пример. Найти ранг матрицы
При вычислении ранга матрицы переходят от вычисления миноров меньших порядков к минорам больших порядков. Если Второй способ основывается на элементарных преобразованиях матрицы. Элементарными преобразованиями называются следующие: 1. перестановка строк (столбцов), 2. умножение строки (столбца) на число, не равное нулю, 3. прибавление к строке (столбцу) другой строки (столбца), умноженной на число, 4. вычеркивание нулевых строк (столбцов), 5. вычеркивание строки (столбца), являющегося линейной комбинацией других строк (столбцов). Элементарные преобразования не изменяют ранга матрицы. Если удастся путем элементарных преобразований привести матрицу к трапециевидной форме, то ее ранг будет равен числу ее ненулевых строк.
При приведении матрицы к трапециевидной форме удобно пользоваться численным методом Гаусса: 1) переставляя строки, добиваемся, чтобы 2) умножаем первую строку на числа ( 3) не трогая первой строки, добиваемся, чтобы 4) умножаем вторую строку на числа ( 5) и т.д. Пример. Найти ранг матрицы
в матрице две ненулевые строки, следовательно, Системы линейных уравнений. П. 1. Основные понятия.
Определение 18. Система уравнений вида
называется системой m линейных уравнений с n неизвестными Если все bi = 0 (i = 1, 2, 3,…, m), то система называется однородной, в противном случае неоднородной. Матрица, состоящая из коэффициентов при неизвестных, называется матрицей системы. Матрица, состоящая из коэффициентов при неизвестных и столбца свободных членов, называется расширенной матрицей системы.
Матричная запись системы линейных уравнений имеет вид:
Определение 19. Система уравнений, имеющая хотя бы одно решение, называется совместной и несовместной, если она не имеет ни одного решения. Определение 20. Система называется определенной, если имеет одно решение, и неопределенной, если решений более одного.
Определение 21. Решением системы (*) называется всякая совокупность чисел Элементарные преобразования системы (только над строками): 1. перестановка уравнений, 2. умножение уравнения на число, отличное от нуля, 3. прибавление к уравнению другого уравнения, умноженного на число. Выполняют элементарные преобразования над расширенной матрицей системы и лишь над строками, так как перестановка столбцов соответствует переобозначению неизвестных. Пп. 1. Метод Крамера (для решения неоднородных систем, когда
Теорема Крамера. Рассмотрим неоднородную систему n линейных уравнений с n неизвестными:
Или в матричной форме Умножим обе части уравнения
– матричный способ решения системы. Формулы Крамера. Если определитель матрицы системы отличен от нуля, то система имеет единственное решение, которое находится по формулам:
где
– определитель матрицы системы,
– определитель, полученный из определителя Пример 1. Решить систему уравнений: Решение. а) Решим систему по формулам Крамера. Найдем определитель матрицы системы: Найдем определители
Найдем решение системы по формулам Крамера:
Ответ: (1, 3, 5). б) Решим систему матричным способом. Найдем обратную матрицу по формуле
Решение неоднородных систем, когда Пп. 2. Метод Гаусса Решение неоднородных систем Одним из наиболее универсальных и эффективных методов решения линейных алгебраических систем является метод Гаусса, который состоит в последовательном исключении неизвестных. Пусть дана система неоднородных уравнений
Процесс решения состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
где На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Прямой ход: Будем считать, что элемент Преобразуем систему, исключив неизвестное
Здесь Аналогичным образом, считая главным элементом Если в процессе решения появляются нулевые уравнения, т.е. уравнения вида Обратный ход заключается в решении ступенчатой системы уравнений, которая, вообще говоря, имеет бесконечное множество решений. В последнем уравнении выражаем первое неизвестное Замечание 1. Если ступенчатая система оказывается треугольной, т.е. Замечание 2. На практике удобнее работать не с системой, а с расширенной матрицей системы (пример см. в методичке Парыгина и др. ч.2, стр. 13).
Примеры. Пример 1. Решить систему линейных уравнений Решение. 1. Метод Гаусса.
~ Система имеет единственное решение. Найдем его, для этого запишем полученную матрицу в виде системы линейных уравнений:
Отсюда Ответ: 2) Формулы Крамера. Найдем определитель матрицы системы:
По формулам Крамера решение системы имеет вид:
Ответ:
Глава 2. Векторная алгебра. Векторы. П.1. Основные определения. Существуют скалярные и векторные величины. Скалярные характеризуются своим численным значением (например, температура, работа, плотность,…), а векторные, кроме численного значения, обладают также направлением в пространстве (например, сила, скорость,…). Определение 1. Вектором называется направленный отрезок

Определение 2. Длиной или модулем вектора Задать вектор – это значит задать его модуль и направление в пространстве. Определение 3. Вектор Определение 4. Векторы
Определение 5. Векторы Определение 6. Единичный вектор, имеющий одинаковое направление с вектором
Определение 7. Вектор, выходящий из начала координат, называется радиус-вектором. Определение 8. Векторы, лежащие в одной плоскости (параллельные одной плоскости), называются компланарными. Определение 9. Если
С помощью параллельного переноса векторы можно перемещать в любое место пространства. Вычитание векторов. Определение 10. Противоположным вектором к вектору Вычесть вектор, значит прибавить противоположный.
а) Правило параллелограмма.
б) Правило треугольника
Вывод из 1 и 2: векторы суммы и разности векторов направлены по диагоналям параллелограмма, построенного на векторах
Таблица скалярного умножения ортов
Пользуясь определением скалярного произведения, составим таблицу скалярного произведения векторов
Примеры. Пример 1. Найти скалярное произведение векторов Решение.
Пример 2. Даны вершины треугольника АВС, где А (–1, –2, 4), В (–4, –2, 0), С (3, –2, 1). Определить его внутренний угол α при вершине В. Решение. Угол при вершине В образуют векторы Пример 3. Проверить перпендикулярность векторов Решение.
Таблица векторного умножения ортов
Примеры. Пример 1. Векторы Решение.
Пример 2. Даны Решение. Из свойства Из основного тригонометрического тождества следует, что Найдем Пример 3. Векторы Решение.
= Пример 4. Даны два вектора Решение. Найдем координаты векторов
Пример 5. Сила Решение. Найдем вектор
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.107.191 (0.205 с.) |
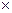 n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов.
n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов.
 , из которых составлена матрица, называются ее элементами, где i – номер строки (
, из которых составлена матрица, называются ее элементами, где i – номер строки ( ), j – номер столбца
), j – номер столбца  , на пересечении которых стоит элемент aij .
, на пересечении которых стоит элемент aij . :
: 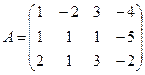 ,
,  ,
,  ,
,  .
. n.
n.
 ,
,  , …,
, …,  образуют главную диагональ, а элементы
образуют главную диагональ, а элементы 
 …,
…,  – побочную диагональ.
– побочную диагональ. , если aij = bij.
, если aij = bij. называется матрица
называется матрица  размерности n
размерности n  ,
, 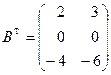 .
.
 .
.
 - матрица-строка,
- матрица-строка, 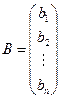 – матрица-столбец.
– матрица-столбец. .
. или
или  или
или 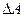 или
или 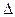 и вычисляется по некоторым правилам, в зависимости от размерности матрицы.
и вычисляется по некоторым правилам, в зависимости от размерности матрицы. .
. Пример.
Пример. 

 .
.
 +
+  +
+  –
–  –
–  –
–  – правило треугольников (правило Саррюса), которое символически можно записать так:
– правило треугольников (правило Саррюса), которое символически можно записать так:












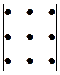 =
= 
 +
+  +
+  –
–  –
–  –
–  = – 10.
= – 10. ;
;  .
. ;
;  .
. .
. 2
2  .
.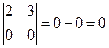 .
.
 .
. .
. .
.
 определителя n- го порядка называется, определитель (n -1) порядка, получаемый вычеркиванием i- ой строки и j -го столбца, на пересечении которых элемент
определителя n- го порядка называется, определитель (n -1) порядка, получаемый вычеркиванием i- ой строки и j -го столбца, на пересечении которых элемент  или
или  .
. .
.  , А 13,
, А 13, 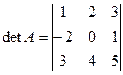 .
.
 .
.  .
.  .
. :
:




 .
. . Определитель матрицы будем называть минором k -го порядка матрицы А.
. Определитель матрицы будем называть минором k -го порядка матрицы А. или
или  .
. ;
; ;
;  ;
; 
 .
. , то всякий отличный от нуля минор порядка
, то всякий отличный от нуля минор порядка  называется базисным минором. Этот метод вычисления ранга матрицы называется методом окаймляющих миноров.
называется базисным минором. Этот метод вычисления ранга матрицы называется методом окаймляющих миноров. и
и  , последнее можно достичь (если в первом столбце нет единиц) путем деления всей строки на
, последнее можно достичь (если в первом столбце нет единиц) путем деления всей строки на  . Первую строку называют рабочей, а элемент
. Первую строку называют рабочей, а элемент  – ведущим.
– ведущим. ), где
), где  , прибавляем ее соответственно ко второй и т.д. m-ой строке, получаем в 1-ом столбце под
, прибавляем ее соответственно ко второй и т.д. m-ой строке, получаем в 1-ом столбце под  и
и  путем деления всей строки на
путем деления всей строки на  или путем перестановки строк. Теперь вторая строка стала рабочей, а элемент
или путем перестановки строк. Теперь вторая строка стала рабочей, а элемент  – ведущим.
– ведущим. ), где
), где  , прибавляем ее соответственно к третей и т.д. m-ой строке, получаем во 2-ом столбце под
, прибавляем ее соответственно к третей и т.д. m-ой строке, получаем во 2-ом столбце под  . Решение.
. Решение. ~ (меняем строки местами)
~ (меняем строки местами) 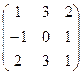 ~ (первую строку прибавляем ко второй)
~ (первую строку прибавляем ко второй)  ~ (первую строку умножаем на (-2) и прибавляем к третьей)
~ (первую строку умножаем на (-2) и прибавляем к третьей)  ~ (прибавляем ко второй строке третью)
~ (прибавляем ко второй строке третью)  ~
~  ,
, .
. (*)
(*) ,
,  , …,
, …,  .
. – матрица системы,
– матрица системы,  – расширенная матрица системы,
– расширенная матрица системы, – столбец свободных членов,
– столбец свободных членов,  – столбец неизвестных.
– столбец неизвестных. .
. ,
,  , …,
, …,  , которая, будучи подставлена в систему (8) вместо неизвестных
, которая, будучи подставлена в систему (8) вместо неизвестных 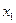 ,
,  , …,
, …, 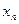 , обращает все уравнения системы в тождества.
, обращает все уравнения системы в тождества. )
)
 .
. , получим
, получим  , поскольку
, поскольку  и
и  , то
, то –
– ,
,  , …,
, …,  ,
,
 –
– –
– заменой j -го столбца столбцом свободных членов,
заменой j -го столбца столбцом свободных членов, 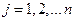 .
.  .
.
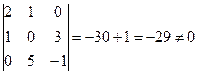 , следовательно, система имеет единственное решение.
, следовательно, система имеет единственное решение. :
:
 ,
, 
 ,
, 
 .
. ,
,  ,
,  .
. .
.








 ;
;



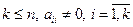 . Коэффициенты
. Коэффициенты  называют главными коэффициентами системы.
называют главными коэффициентами системы. ; (если
; (если  , то первым в системе запишем то уравнение, в котором коэффициент при
, то первым в системе запишем то уравнение, в котором коэффициент при 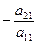 и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на
и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на 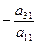 и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
 ,
, 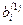
 – новые значения коэффициентов и правых частей, которые получаются после первого шага.
– новые значения коэффициентов и правых частей, которые получаются после первого шага. , исключим неизвестное
, исключим неизвестное  из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока возможно.
из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока возможно. , их отбрасывают. Если же появляются уравнения
, их отбрасывают. Если же появляются уравнения  , а
, а 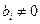 , то это говорит о том, что система несовместна.
, то это говорит о том, что система несовместна.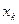 через остальные неизвестные
через остальные неизвестные  . Затем подставляем значение
. Затем подставляем значение 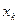 в предпоследнее уравнение системы и выражаем
в предпоследнее уравнение системы и выражаем  через
через  , то система имеет единственное решение.
, то система имеет единственное решение. двумя способами.
двумя способами. ~
~  ~
~  ~
~  ~
~ 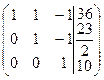
 .
.  .
. .
.
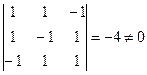 , следовательно, существует единственное решение. Найдем определители
, следовательно, существует единственное решение. Найдем определители  :
: ,
,  ,
, 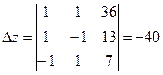 .
. ,
, 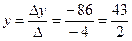 ,
,  .
. с начальной точкой А и конечной В.
с начальной точкой А и конечной В. 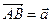
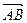 называется длина отрезка
называется длина отрезка 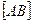 . Обозначается
. Обозначается 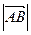 .
.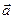 называется единичным, если
называется единичным, если 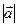 =1. Вектор
=1. Вектор  . Нулевой вектор
. Нулевой вектор 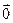 имеет любое направление.
имеет любое направление.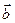 называются коллинеарными, если они параллельны одной прямой, обозначаются
называются коллинеарными, если они параллельны одной прямой, обозначаются 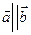 . Векторы
. Векторы 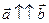 – сонаправлены.
– сонаправлены. 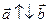 – противоположно направлены.
– противоположно направлены.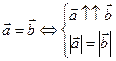 .
.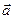 , называется ортом вектора
, называется ортом вектора  , если
, если  .
.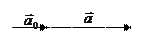
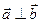 , векторы называются ортогональными.
, векторы называются ортогональными. называется вектор
называется вектор  , причем
, причем 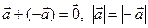 .
.
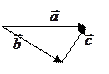


 Углы
Углы  ,
,  ,
, 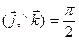 ,
, 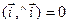 ,
, 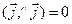 ,
, ; тогда
; тогда  ; длины ортов равны
; длины ортов равны 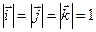 .
. :
:



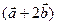 и
и  , если известно, что
, если известно, что 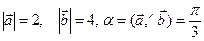 .
. 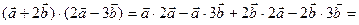



 –84.
–84. и
и  ,
, 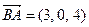 ,
, 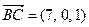 . Длины векторов равны
. Длины векторов равны 
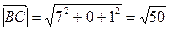 , тогда по формуле (6):
, тогда по формуле (6): 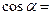
 =
= 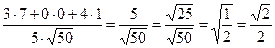 , то есть α = 450.
, то есть α = 450.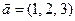 и
и  .
.
 . Найдем
. Найдем  , то есть векторы не перпендикулярны.
, то есть векторы не перпендикулярны. 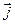

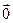



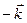



 и
и  образуют угол
образуют угол 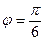 . Зная
. Зная 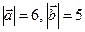 , вычислить
, вычислить  .
. =
=  . Ответ: 15.
. Ответ: 15. ,
, 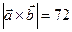 . Вычислить скалярное произведение векторов
. Вычислить скалярное произведение векторов 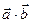 .
.  .
.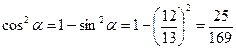 .
. :
:  . По определению найдем скалярное произведение векторов:
. По определению найдем скалярное произведение векторов:  =
= 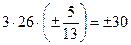
 и
и 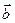 образуют угол
образуют угол 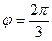 . Зная
. Зная 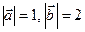 , вычислить
, вычислить  .
. 

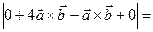
 3
3 
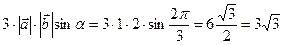 .
.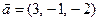 и
и 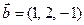 . Найти координаты векторного произведения векторов
. Найти координаты векторного произведения векторов 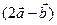 и
и 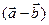 .
. 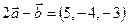 ,
,  .
.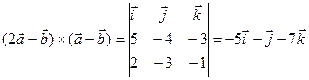 . Ответ:
. Ответ: 
 приложена к точке В (4, -2, 3). Определить момент этой силы относительно точки А (3, 2, -1) и его величину.
приложена к точке В (4, -2, 3). Определить момент этой силы относительно точки А (3, 2, -1) и его величину.  .
.