
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение однородных систем методом Гаусса
Однородная система линейных уравнений
всегда совместна, так как она всегда имеет нулевое решение
Теорема Кронекера - Капелли для однородной системы: 1) если 2) если Пример. Решить систему линейных уравнений: Решение. Запишемматрицу системы: ~ отсюда
Система имеет три базисные неизвестные: Выразим базисные неизвестные через свободную переменную, начиная с последнего уравнения:
Ответ: Общее решение системы: Решение неоднородных систем методом Гаусса Пример 1. Решить систему уравнений: Решение. ~ Проверим условия теоремы Кронекера-Капелли:
Ответ: {(1, 3, 5)}. Пример 2. Решить систему уравнений: Решение. ~ Ответ: Примеры. Пример 1. Решить систему линейных уравнений Решение. 1. Метод Гаусса.
~ Система имеет единственное решение. Найдем его, для этого запишем полученную матрицу в виде системы линейных уравнений:
Отсюда Ответ: 2) Формулы Крамера. Найдем определитель матрицы системы:
По формулам Крамера решение системы имеет вид:
Ответ:
Глава 2. Векторная алгебра. Векторы. П.1. Основные определения. Существуют скалярные и векторные величины. Скалярные характеризуются своим численным значением (например, температура, работа, плотность,…), а векторные, кроме численного значения, обладают также направлением в пространстве (например, сила, скорость,…).
Определение 1. Вектором называется направленный отрезок

Определение 2. Длиной или модулем вектора Задать вектор – это значит задать его модуль и направление в пространстве. Определение 3. Вектор Определение 4. Векторы
Определение 5. Векторы Определение 6. Единичный вектор, имеющий одинаковое направление с вектором
Определение 7. Вектор, выходящий из начала координат, называется радиус-вектором. Определение 8. Векторы, лежащие в одной плоскости (параллельные одной плоскости), называются компланарными. Определение 9. Если
С помощью параллельного переноса векторы можно перемещать в любое место пространства.
|
|||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 62; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.144.197 (0.008 с.) |

 =
=  = …=
= …= 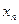 = 0, которое называется тривиальным. Для этой системы справедливо, что
= 0, которое называется тривиальным. Для этой системы справедливо, что  .
.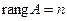 , то система имеет единственное решение – нулевое
, то система имеет единственное решение – нулевое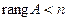 , то система имеет бесконечное множество решений, среди которых есть и ненулевые.
, то система имеет бесконечное множество решений, среди которых есть и ненулевые.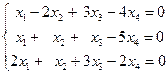 .
. ~
~ 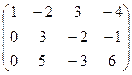 ~
~ 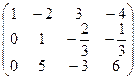 ~
~  ~
~  ,
, т.к. три ненулевые строки. Количество неизвестных n = 4, т.е.
т.к. три ненулевые строки. Количество неизвестных n = 4, т.е.  , следовательно, по теореме Кронекера - Капелли система имеет бесконечное множество решений. Найдем его. Запишем полученную матрицу в виде системы уравнений:
, следовательно, по теореме Кронекера - Капелли система имеет бесконечное множество решений. Найдем его. Запишем полученную матрицу в виде системы уравнений: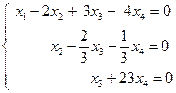 .
.  и одну свободную
и одну свободную 
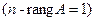 .
. ,
,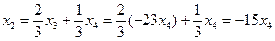 ,
, 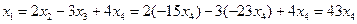 .
. . Частное решение системы при
. Частное решение системы при  :
:  .
.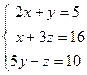 .
.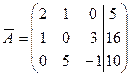 ~
~ 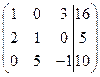 ~
~ 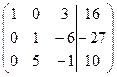 ~
~ ~
~ 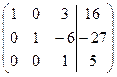 .
.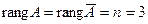 , следовательно, система имеет единственное решение. Найдем его. Запишем полученную матрицу в виде системы уравнений:
, следовательно, система имеет единственное решение. Найдем его. Запишем полученную матрицу в виде системы уравнений: . Отсюда
. Отсюда 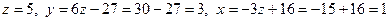 .
.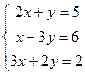 .
. ~
~ 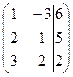 ~
~ 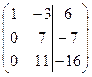 ~
~ 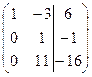 ~
~ . Проверим условия теоремы Кронекера-Капелли:
. Проверим условия теоремы Кронекера-Капелли:  то есть,
то есть, 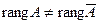 , следовательно, система не имеет решений.
, следовательно, система не имеет решений.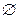 .
. двумя способами.
двумя способами. ~
~  ~
~  ~
~  ~
~ 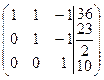
 .
.  .
. .
.
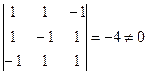 , следовательно, существует единственное решение. Найдем определители
, следовательно, существует единственное решение. Найдем определители  :
: ,
,  ,
, 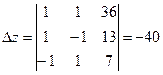 .
. ,
, 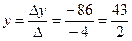 ,
,  .
.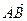 с начальной точкой А и конечной В.
с начальной точкой А и конечной В. 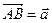
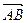 называется длина отрезка
называется длина отрезка 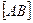 . Обозначается
. Обозначается 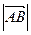 .
.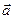 называется единичным, если
называется единичным, если 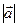 =1. Вектор
=1. Вектор  . Нулевой вектор
. Нулевой вектор 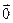 имеет любое направление.
имеет любое направление.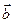 называются коллинеарными, если они параллельны одной прямой, обозначаются
называются коллинеарными, если они параллельны одной прямой, обозначаются 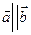 . Векторы
. Векторы 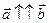 – сонаправлены.
– сонаправлены. 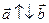 – противоположно направлены.
– противоположно направлены.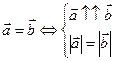 .
.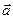 , называется ортом вектора
, называется ортом вектора  , если
, если  .
.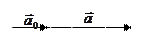
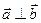 , векторы называются ортогональными.
, векторы называются ортогональными.


