Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 9. Множественная регрессия
Пусть теперь имеется случайный вектор Z = [ x 1,…, xk, y 1,…, yr ] T, который подчиняется (k+ r) – мерному нормальному закону Nk+r (a, Σ) с известными вектором средних a и ковариационной матрицей Σ. Рассмотрим случай, когда первые k компонент x 1,…, xk вектора Z наблюдаются в эксперименте, а оставшиеся компоненты y 1,…, yr являются ненаблюдаемыми. Требуется получить оценки ненаблюдаемых компонент. Пример 9.1. В лабораторных условиях текущее состояние смазочных материалов контролируется по 16 параметрам и имеется достаточная база данных для оценки их средних и их ковариационной матрицы. В полевых условиях экспресс-анализ позволяет проконтролировать только 7 параметров. На основе знания значений этих 7 параметров требуется оценить оставшиеся 9 показателей. Пример 9.2. Для технологической установки имеется база данных, содержащая значения выходных параметров (продукта) при различных комбинациях входных и управляющих параметров. Предположим, что эта база достаточна для оценивания средних и ковариационной матрицы всего вектора контролируемых показателей. а) Заданы текущие значения входных (сырья) и управляющих параметров. Требуется получить прогноз вектора выходных параметров установки (продукта). б) Заданы требуемые значения выходных параметров и используемые в настоящий момент значения управляющих параметров. Требуется сформировать требования к входным параметрам (сырью). в) Заданы текущие значения входных параметров (свойства сырья). Требуется найти комбинацию управляющих параметров, оптимизирующих целевую функцию, которая отражает свойства выходных показателей (например, в единицах стоимости).
Согласно поставленным условиям, средние и ковариационная матрица вектора Z имеют блочную структуру:
Будем сразу рассматривать центрированные величины:
Требуется определить матрицу C размерности
В проведенных преобразованиях использован тот факт, что если оба матричных произведения AB и BA имеют смысл, то tr (AB) = tr (BA). Функция матричного аргумента G (C) является выпуклой и имеет единственный экстремум – минимум. Вычислим ее производную по матрице С и приравняем ее нулю, используя очевидное соотношение
Возвращаясь к исходным величинам X, Y, получаем уравнение множественной линейной регрессии Y на X:
(сравни с формулой (8.5)). Ковариационную матрицу ошибок прогноза в компактной форме представить не удается, но можно вычислить ее след (упрощение достигается за счет того, что tr (AB) = tr (BA)):
(сравни с формулой (6)). На формуле (9.3) основаны различные определения множественного коэффициента корреляции. Аналогичная техника позволяет решить, например, такую задачу. Имеется одна ненаблюдаемая компонента. Требуется построить линейную комбинацию наблюдаемых компонент, в максимальной степени коррелированную с данной ненаблюдаемой. Пример 9.5. Требуется спрогнозировать биржевой курс акций данной компании по курсам ряда других компаний с некоторым отставанием во времени.
Задачи
Пример выполнения работы
Рис.9.1. Прогноз третьей (ненаблюдаемой) компоненты по первым двум (наблюдаемым)
|
|||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 87; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.81.166 (0.009 с.) |
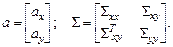
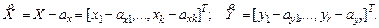
 , доставляющую минимум функции потерь G (C), которая представляет собой сумму дисперсий погрешностей прогноза:
, доставляющую минимум функции потерь G (C), которая представляет собой сумму дисперсий погрешностей прогноза: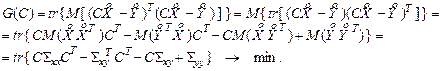 (9.1)
(9.1) При дифференцировании нужно все время иметь в виду, что производная матричной функции по матрице С размерности
При дифференцировании нужно все время иметь в виду, что производная матричной функции по матрице С размерности 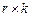 .
.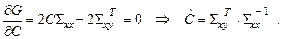
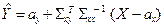 (9.2)
(9.2)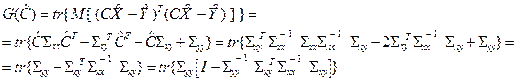 (9.3)
(9.3)