Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И их оценок по схеме Пирсона
Таблица 1
Всякий математический результат, предназначенный для непосредственного практического применения, должен обладать свойством устойчивости по отношению к небольшим отклонениям от исходных предположений. Для обозначения этого свойства в настоящее время принято использовать термин «робастность». В математической статистике понятию робастности придают точный смысл, рассматривая ее как непрерывность распределения статистик решающих правил при введении той или иной топологии в окрестности исходной модели. Другой подход состоит в использовании широко распространенного в общей теории статистических решений и в теории игр принципа минимакса. Из сказанного неизбежно вытекает, что традиционно используемые методы обработки экспериментальных данных, в частности, методы, основанные на предположении нормальности рассматриваемых процессов, уже в силу исторического «естественного отбора» должны обладать ярко выраженными свойствами робастности. Это действительно так, и далее будет показано, что при применении к очень широким классам моделей, т.е. при работе в условиях очень большой априорной неопределенности робастные решения часто сводятся к известным процедурам нормальной теории. При этом любая дополнительная информация о модели, снижающая уровень априорной неопределенности, позволяет повысить точность и достоверность принимаемого решения. Эти соображения приводят к построению иерархической системы решающих правил, отражающих иерархию уровней неопределенности, которая позволяет в самых разных ситуациях найти оптимальное соотношение между предположениями, закладываемыми в исходную модель, и статистической информацией, извлекаемой из данных на основе этой модели. В то же время, существуют области, в которых традиционная теория работает плохо или даже полностью отказывает. К ним прежде всего относятся задачи обработки измерений, содержащих аномальные выбросы или помехи (выпадающие измерения). Обсуждение таких проблем будет проведено ниже на примере простейшей модельной задачи оценивания центра симметричного распределения. В широком плане такие постановки приводят к формированию различных комплексов условий априорной неопределенности, по отношению к которым исследователю и приходится находить оптимальные статистические решения.
Оценка любого параметра теоретического распределения на практике выступает как конкретное число, а в теории – как случайная величина, функция от выборочных значений x 1,…, xn. Любая такая функция называется статистикой. Какими свойствами должна обладать статистика, чтобы ее можно было использовать в качестве оценки некоего параметра c теоретического распределения? Любая статистика является случайной величиной с каким-то своим законом распределения, поэтому можно изучать этот закон, а также ее среднее, дисперсию и т.д. Ясно, что она должна быть близка к истинному значению оцениваемого параметра и возможное отклонение должно уменьшаться при
(сходимость по вероятности, но можно рассматривать и другие типы сходимости). В частности, доказывается, что предложенная К.Пирсоном оценка для F (x) состоятельна, а его оценки для моментов α k теоретического распределения являются состоятельными при условии конечности моментов удвоенного порядка α2 k. · Несмещенность. Статистика g=g(x 1,…, xn) называется несмещенной оценкой параметра c, если математическое ожидание M g(x 1,…, xn)= c. Часто рассматривают асимптотическую несмещенность:
которая является несмещенной. Как правило, все нелинейные статистики дают смещенные оценки, которые исправляются с помощью специально подобранных множителей.
Пусть g n и gn – две несмещенные оценки одного и того же параметра c. Относительной эффективностью g n относительно gn называется отношение их дисперсий:
Обычно рассматривают асимптотическую эффективность при Важным понятием теории оценок является понятие доверительной оценки параметра c. Доверительным интервалом [g1, g2] с коэффициентом доверия (надежности) α называется пара статистик g1=g1(x 1,…, xn) и g2=g2(x 1,…, xn) таких, что
Практическая схема применения введенных понятий обычно такова. Имеется набор измерений x 1,…, xn. Принимаются предположения, что этот набор можно рассматривать как выборку и из тех или иных теоретических или экспериментальных соображений подбирается семейство функций, к которому может принадлежать теоретический закон F (x). Если это семейство параметрическое, то нужно найти оценки его параметров и, тем самым, найти оценку F (x). Если семейство слишком обширно, приходится пользоваться эмпирической функцией распределения F* (x), стараясь модернизировать ее с учетом всей доступной априорной информации. Зная оценку F (x) и контролируя ее точность, можно делать на ее основе различные статистические выводы, в частности, решать задачи управления и прогнозирования.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.63.114 (0.009 с.) |
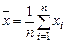
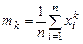

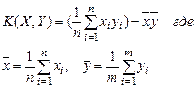
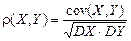
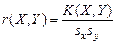

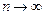 . Сформулируем эти свойства более точно.
. Сформулируем эти свойства более точно.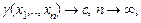
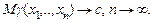
 Доказывается, что введенные К.Пирсоном оценки для начальных моментов и для центральных моментов при известном математическом ожидании a являются несмещенными. В то же время, если в оценке, например, для дисперсии математическое ожидание заменено на его оценку по той же выборке, то такая оценка имеет смещение, которое стремится к нулю при
Доказывается, что введенные К.Пирсоном оценки для начальных моментов и для центральных моментов при известном математическом ожидании a являются несмещенными. В то же время, если в оценке, например, для дисперсии математическое ожидание заменено на его оценку по той же выборке, то такая оценка имеет смещение, которое стремится к нулю при 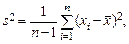
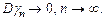 Как правило, для любого параметра теоретического распределения существует оценка максимального правдоподобия, у которой дисперсия убывает быстрее всего, хотя и встречаются особо сложные ситуации, когда оценка максимального правдоподобия не существует. В то же время, часто приходится использовать упрощенные оценки с худшими свойствами.
Как правило, для любого параметра теоретического распределения существует оценка максимального правдоподобия, у которой дисперсия убывает быстрее всего, хотя и встречаются особо сложные ситуации, когда оценка максимального правдоподобия не существует. В то же время, часто приходится использовать упрощенные оценки с худшими свойствами.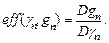
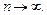 Чаще всего в качестве второй оценки gn берут теоретически оптимальную оценку максимального правдоподобия и сравнивают с ней другие возможные оценки g n. При этом эффективность меняется от 0 до 1. Если, например, эффективность g n равна 80%, это значит, что при ее использовании вместо gn теряется 20% информации, для достижения заданной точности придется получить на 20% измерений больше.
Чаще всего в качестве второй оценки gn берут теоретически оптимальную оценку максимального правдоподобия и сравнивают с ней другие возможные оценки g n. При этом эффективность меняется от 0 до 1. Если, например, эффективность g n равна 80%, это значит, что при ее использовании вместо gn теряется 20% информации, для достижения заданной точности придется получить на 20% измерений больше.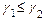 ;
;