Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 8. Оптимальный линейный прогноз
Пусть имеется случайная величина ηс известным законом распределения. Рассмотрим задачу о построении прогноза Основной довод в пользу этого принципа состоит в простоте вычислений, к которым он приводит. Получающийся на его основе результат предсказания называют оптимальным среднеквадратным прогнозом. Решая уравнение получаем Пусть теперь имеется двумерный случайный вектор определив коэффициенты Получающийся на его основе результат предсказания называют оптимальным в среднем квадратическом линейным прогнозом. Определение оптимальных значений коэффициентов
т.е. Первое уравнение показывает, что математическое ожидание ошибки прогноза равно нулю, так что условие (2) автоматически обеспечивает несмещенность прогноза. Подставляя значение Коэффициент при Таким образом,
Процедуру построения прогноза Ее называют прямой среднеквадратической регрессии (СКР) Заметим, что прямая среднеквадратической регрессии ξ на η, с помощью которой можно строить прогноз и совпадает с
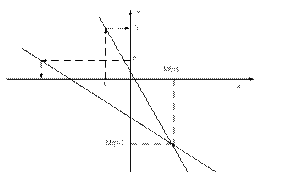
Рис.8.1. Прямая среднеквадратической регрессии η на ξ
Подставив найденные значения
находим:
Это выражение, равное (в силу несмещенности) дисперсии ошибки прогноза
Рис.8.2. Прямые среднеквадратической регрессии η на ξ и ξ на η Задачи
Пример выполнения работы
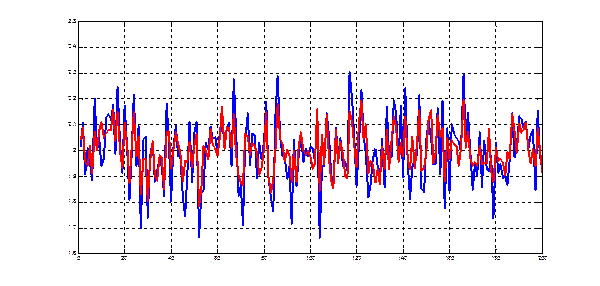
Рис.8.1. Прогноз второй (ненаблюдаемой) компоненты по первой (наблюдаемой)
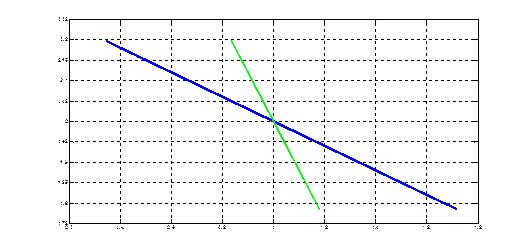
Рис.8.2. Прямые среднеквадратической регрессии компонент друг на друга
|
||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.6.75 (0.008 с.) |
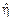 значения, которое величина η может принять в эксперименте. Это прогнозируемое значение должно быть определено на основе некоторого критерия оптимальности, состоящего в том, что распределение случайной величины
значения, которое величина η может принять в эксперименте. Это прогнозируемое значение должно быть определено на основе некоторого критерия оптимальности, состоящего в том, что распределение случайной величины 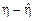 , представляющей собой ошибку прогноза, должно быть как можно сильнее сконцентрировано вблизи нуля. Вообще говоря, для каждого закона распределения существует своя, ему внутренне присущая мера рассеяния, однако можно рассматривать и универсальные меры, применимые к широким классам распределений. Выбирая в качестве такой универсальной меры рассеяния среднее значение (математическое ожидание) квадрата ошибки прогноза, получаем в качестве условия оптимальности принцип наименьших квадратов:
, представляющей собой ошибку прогноза, должно быть как можно сильнее сконцентрировано вблизи нуля. Вообще говоря, для каждого закона распределения существует своя, ему внутренне присущая мера рассеяния, однако можно рассматривать и универсальные меры, применимые к широким классам распределений. Выбирая в качестве такой универсальной меры рассеяния среднее значение (математическое ожидание) квадрата ошибки прогноза, получаем в качестве условия оптимальности принцип наименьших квадратов: 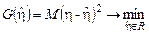 .
.  (8.1)
(8.1)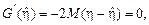
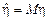 , так что математическое ожидание ошибки прогноза
, так что математическое ожидание ошибки прогноза 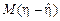 равно нулю. Такой прогноз называют несмещенным. Подставляя найденное значение
равно нулю. Такой прогноз называют несмещенным. Подставляя найденное значение 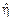 в (8.1), видим, что
в (8.1), видим, что 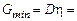
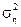 .
.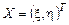 с заданным двумерным законом распределения. Предположим, что компонента
с заданным двумерным законом распределения. Предположим, что компонента 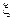 вектора X наблюдается в эксперименте, а компонента η ненаблюдаема. Требуется построить процедуру предсказания (оценивания) η в виде линейной функции ξ
вектора X наблюдается в эксперименте, а компонента η ненаблюдаема. Требуется построить процедуру предсказания (оценивания) η в виде линейной функции ξ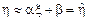 ,
,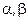 на основе некоторого критерия оптимальности. Принцип наименьших квадратов приводит в этом случае к критериальной функции
на основе некоторого критерия оптимальности. Принцип наименьших квадратов приводит в этом случае к критериальной функции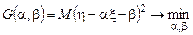 . (8.2)
. (8.2)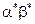 из условия (8.2) сводится к решению системы уравнений
из условия (8.2) сводится к решению системы уравнений
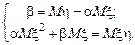


 из первого уравнения во второе, получаем
из первого уравнения во второе, получаем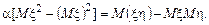
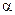 в этом выражении равен, очевидно, дисперсии
в этом выражении равен, очевидно, дисперсии 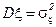 , свободный член – ковариации
, свободный член – ковариации 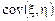 , которую удобно выразить через коэффициент корреляции
, которую удобно выразить через коэффициент корреляции 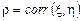 :
: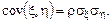

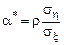 ;
; 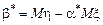 ; (8.3)
; (8.3) 
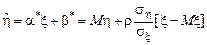 .
.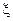 удобно рассматривать в геометрической форме. Построим на плоскости хОу прямую
удобно рассматривать в геометрической форме. Построим на плоскости хОу прямую
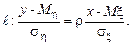 (8.4)
(8.4)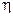 на
на 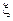 . Откладывая на оси Ох значение
. Откладывая на оси Ох значение 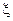 и перенося его с помощью прямой
и перенося его с помощью прямой 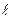 на ось О у, получаем прогноз
на ось О у, получаем прогноз 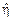 (рис.8.1).
(рис.8.1).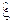 по данному значению η, имеет уравнение
по данному значению η, имеет уравнение 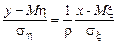 (8.5)
(8.5) только в вырожденном случае
только в вырожденном случае  Эти две прямые пересекаются в точке с координатами
Эти две прямые пересекаются в точке с координатами 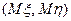 - рис.8.2.
- рис.8.2.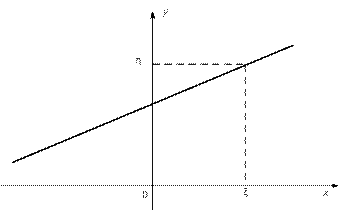
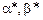 из (8.3) в выражение для G и используя обозначения
из (8.3) в выражение для G и используя обозначения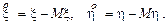
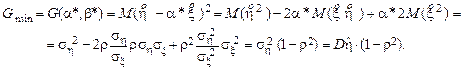 (8.6)
(8.6)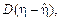 называют остаточной дисперсией величины η. Из него следует, что если ρ=0, т.е. величины ξ и η некоррелированы, то никакая линейная функция от ξ не дает возможности уменьшить дисперсию ошибки прогноза, она остается такой же, как и в отсутствии информации о ξ. Если же
называют остаточной дисперсией величины η. Из него следует, что если ρ=0, т.е. величины ξ и η некоррелированы, то никакая линейная функция от ξ не дает возможности уменьшить дисперсию ошибки прогноза, она остается такой же, как и в отсутствии информации о ξ. Если же 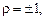 то остаточная дисперсия равна нулю, т.е. между величинами величины ξ и η существует точная линейная связь. В этом смысле коэффициент корреляции ρ можно рассматривать как меру, определяющую тесноту линейной связи между ξ и η.
то остаточная дисперсия равна нулю, т.е. между величинами величины ξ и η существует точная линейная связь. В этом смысле коэффициент корреляции ρ можно рассматривать как меру, определяющую тесноту линейной связи между ξ и η.