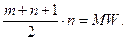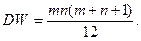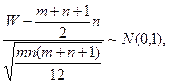Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 7. Непараметрические методы
Непараметрическая статистика – это собрание статистических приемов, которые не используют предположение о том, что теоретическое распределение принадлежит к известному параметрическому семейству. Обычно делаются только самые общие предположения типа непрерывности и, возможно, симметричности. Непараметрическая статистика включает два основных раздела:
Рангом числа Результаты наблюдений Имеется несколько серьёзных аргументов в пользу рассмотрения вместо самих величин xi их рангов ri. При замене численных значений xi их рангами неизбежно происходит потеря информации. Тем не менее, прежде всего необходимо разобраться, что могут представлять собой величины Шкалы измерений
В математическом смысле шкалой называют правило, по которому состояния системы характеризуются числами. Итак, шкала — это переход от физического (или другого) объекта к числу. В данном смысле шкалой будет любая календарная система - моменту времени приписывается определенная дата. Шкалу представляет собой и принятая в школе система оценок, выставляемых ученикам в зависимости отих успехов. Упомянутые шкалы - длин, температур, времени, успехов — различаются не только по содержанию. Между ними есть и важные формальные различия. Результатом измерения в любой шкале является число. С числами можно проводить арифметические и другие операции. Результаты некоторых операций имеют содержательный смысл и истолковываются в рамках данной шкалы. Допустим, чтомы измеряем длины предметов. Если х и у - длины отрезков а и b, то х + у - длина отрезка, полученного приставлением а к b,
Если же х и у — две календарные даты, причем х > у, то х – у имеет смысл - это время, прошедшее от одного события до другого. Однако х + у, ху, х/у и т. п. содержательного смысла лишены. Для показателей по шкале успехов еще меньше осмысленных соотношений: осмысленно их можно лишь сравнивать по величине, т. е. из соотношения отметок х < у для учеников а и b можно лишь заключить, что а учится хуже, чем b. Если же у - х = 1, то утверждение «успехи b на 1 выше, чем успехи а» не объясняет, каково различие между ними. Шкала успехов служит примером порядковой (ранговой) шкалы. Выделяют еще номинальную шкалу, где числа служат всего лишь для различения отдельных возможностей, как бы для их названия. Никаких содержательных соотношений, кроме х = у и х Если x 1,…, xn – действительно числа, результаты измерений, то среди них могут содержаться грубые промахи, аномальные измерения. Даже одно такое аномальное значение может увести далеко в сторону большинство статистик – как оценок, так и статистик критериев (критериальных функций). В то же время, на ранговую структуру выборки оно окажет минимальное воздействие. Ранговые методы всегда ориентируются на основное ядро выборки и мало чувствительны к далеко выпадающим значениям. Если Ранговые методы. Критерий Вилкоксона и медиана Ходжеса-Леман а
Пусть
Для проверки гипотезы однородности наиболее известен критерий Стьюдента, основанный на сравнении средних значений обеих выборок. Для того, чтобы получаемые на его основе выводы были справедливы, нужно, чтобы обе выборки имели близкое к гауссовому распределение с одной и той же дисперсией. Можно применять для проверки Н и критерий Смирнова, основанный на разности эмпирических функций распределения, построенных по каждой выборке отдельно. Критерий Смирнова - чисто непараметрический. Для того, чтобы он был применим, необходима лишь непрерывность истинных функций распределения F и G. Более того, вероятность того, что различие между F и G будет замечено, если оно вообще существует, растет и приближается к 1 при неограниченном увеличении объемов выборок т и п. К сожалению, скорость роста этой вероятности невелика, так что при умеренных значениях т и п мощность критерия Смирнова мала. Мы хотим применить критерии, основанные на рангах. Для этого объединяем обе выборки в одну группу и ранжируем наблюдения. Достаточно знать ранги только игреков, поскольку ранги иксов можно по ним восстановить - это оставшиеся числа из последовательности 1, 2,..., m + n. Обозначим ранги игреков через Легко понять, что при справедливости гипотезы Н в качестве рангов Остается выбрать подходящую функцию рангов, на которой основывать проверку H. Для этого, как всегда, надо подумать о конкурирующих гипотезах, т.е. о том, каким образом может нарушаться H. Рассмотрим наиболее удобную для ранговых методов возможность: нарушение равенства F= G в пользу F< G. Таким соотношение между F и G будет, в частности, в том случае, когда G является «сдвигом» F, т. е. при Пример. Сравниваются длительности плавки в мартеновской печи при работе по стандартной и усовершенствованной технологиям. Естественно считать, что Мы надеемся, что сокращение длительности плавки действительно происходит. Используем обычный логический прием - рассуждение от противного. Предположим, что θ=0, т. е. F = G. Если статистический материал заставит нас отвергнуть это предложение, придется признать, что θ в самом деле положительно. Надо, следовательно, проверить гипотезу H против альтернативы F< G. Если G действительно превосходит F, т. е. если P (xi < x) < P (yi < x), то элементы выборки
{1, 2,..., т + п }. Поэтому статистика Это правило было предложено в 1945 году и послужило отправной точкой для всей обширной области ранговых процедур. По имени ее автора статистика W = r1+…+ rn называется статистикой Вилкоксона, а основанный на W критерий - критерием Вилкоксона. Мы выяснили, каково должно быть поведение W при F< G . Поэтому мы отвергнем H, если W окажется меньше критического значения Wкрит или равным ему. Это критическое значение выбираем так, чтобы Если конкурентом однородности служит возможность F> G, признаком нарушения Н служит слишком большая величина W. Часто применяют двусторонний критерий Вилкоксона, по которому гипотеза Н отвергается, если наблюденное значение выходит за критические значения Значение α подбирают так, чтобы Исследования показали, что мощность критерия Вилкоксона против рассмотренных здесь альтернатив намного превосходит мощность критерия Смирнова. Однако против многих других альтернатив критерий W бессилен, в то время как критерий Смирнова обнаруживает (при неограниченных объемах выборок) любое различие. Легко увидеть, что в объединенной выборке сумма всех рангов равна
так что на каждое из (m + n) измерений приходится «средний ранг» (m + n+ 1)/2. Мы следим за положением
Дисперсия статистики W вычисляется несколько сложнее:
При достаточно больших m, n (больше 20) распределение W хорошо аппроксимируется нормальным законом:
при меньших m, n есть специальные таблицы. Составить представление о возможностях W можно, рассмотрев какие-либо конкретные F и G. Пусть
Задачи
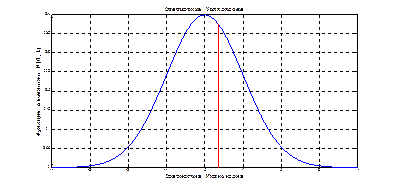
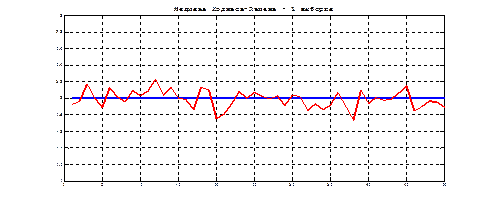
Пример выполнения работы
Рис.7.1. Статистика критерия Уилкоксона и её гауссова аппроксимация
Рис.7.2. Медиана Ходжеса-Лемана – 50 имитаций
|
||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.39.32 (0.029 с.) |
 в группе
в группе 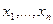 называют тот номер, который оно получает при упорядочении всей группы по возрастанию. Так, ранг 1 получает наименьшее из наблюдений, ранг 2 - наименьшее из оставшихся, и т. д. Ранг п достается самому большому из чисел
называют тот номер, который оно получает при упорядочении всей группы по возрастанию. Так, ранг 1 получает наименьшее из наблюдений, ранг 2 - наименьшее из оставшихся, и т. д. Ранг п достается самому большому из чисел 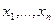 .
.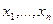 обычно предполагаются распределенными непрерывно, поэтому совпадения среди чисел
обычно предполагаются распределенными непрерывно, поэтому совпадения среди чисел 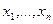 есть одинаковые, они получают общий ранг, обычно средний.
есть одинаковые, они получают общий ранг, обычно средний.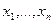 , которые обычно трактуются как результаты некоторых измерений.
, которые обычно трактуются как результаты некоторых измерений. 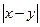 — разница длин отрезков, ху — площадь прямоугольника, образованного этими отрезками, и т. п. Однако ху или, например, log(x)для нас не имеют содержательного толкования.
— разница длин отрезков, ху — площадь прямоугольника, образованного этими отрезками, и т. п. Однако ху или, например, log(x)для нас не имеют содержательного толкования.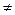 у, между такими числами нет. Конечно, выбор чисел (т. е. номинальной шкалы) вместо реальных имен или других способов идентификации не обязателен, более того, может привести к недоразумениям.
у, между такими числами нет. Конечно, выбор чисел (т. е. номинальной шкалы) вместо реальных имен или других способов идентификации не обязателен, более того, может привести к недоразумениям.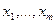 и
и 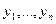 - две независимые выборки. Неизвестные законы распределения случайных величин
- две независимые выборки. Неизвестные законы распределения случайных величин 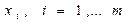 и
и 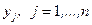 обозначим через
обозначим через 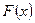 и
и 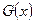 соответственно. По данным наблюдениям хотим проверить гипотезу однородности H:
соответственно. По данным наблюдениям хотим проверить гипотезу однородности H: 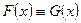 .
.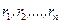 . Статистика для проверки Н должна быть функцией этих чисел.
. Статистика для проверки Н должна быть функцией этих чисел.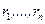 с равными вероятностями могут появляться любые п чисел из 1, 2,..., т + п. Это дает возможность рассчитать при выполнении H закон распределения любой статистики, основанной на рангах. Это обстоятельство — основная причина перехода к рангам, причина универсальности и простоты ранговых методов.
с равными вероятностями могут появляться любые п чисел из 1, 2,..., т + п. Это дает возможность рассчитать при выполнении H закон распределения любой статистики, основанной на рангах. Это обстоятельство — основная причина перехода к рангам, причина универсальности и простоты ранговых методов.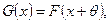
 . Такие альтернативы реально возникают в некоторых задачах, например, при измерении какой-то величину, обладающей естественной изменчивостью, при различных управляющих воздействиях.
. Такие альтернативы реально возникают в некоторых задачах, например, при измерении какой-то величину, обладающей естественной изменчивостью, при различных управляющих воздействиях.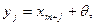 где
где 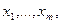
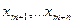 последовательность независимых одинаково распределенных случайных величин, θ - закономерное изменение (сокращение, если θ<0) длительности плавки. Конечно, величина θ не наблюдается. Наблюдаются выборки
последовательность независимых одинаково распределенных случайных величин, θ - закономерное изменение (сокращение, если θ<0) длительности плавки. Конечно, величина θ не наблюдается. Наблюдаются выборки 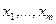 и
и  (Если θ>0, альтернативой к H служит F> G).
(Если θ>0, альтернативой к H служит F> G).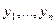 имеют тенденцию располагаться левее элементов выборки
имеют тенденцию располагаться левее элементов выборки 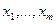 . Это значит, что ранги игреков имеют тенденцию располагаться в левой части последовательности
. Это значит, что ранги игреков имеют тенденцию располагаться в левой части последовательности в случае F< G склонна к меньшим значениям, нежели в случае F= G. Из этого следует статистическое правило: отвергать гипотезу F= G (в пользу F < G), если r1 + … rn слишком мала.
в случае F< G склонна к меньшим значениям, нежели в случае F= G. Из этого следует статистическое правило: отвергать гипотезу F= G (в пользу F < G), если r1 + … rn слишком мала.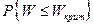 при H была малой.
при H была малой.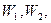 т. е. если не происходит событие
т. е. если не происходит событие 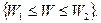 Критические значения
Критические значения  находят по таблицам из условия
находят по таблицам из условия
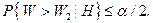
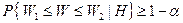 была достаточно близка к 1.
была достаточно близка к 1.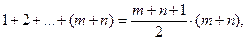
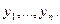 Если гипотеза H верна, то они распределены в объединенной выборке приблизительно равномерно, так что на их сумму приходится в среднем величина
Если гипотеза H верна, то они распределены в объединенной выборке приблизительно равномерно, так что на их сумму приходится в среднем величина