Метод максимального правдоподобия Р.Фишера

        Английский биолог Рональд Фишер в начале XX века предложил метод статистического оценивания неизвестных параметров, который, как выяснилось при развитии теории статистических выводов, в большинстве ситуаций является оптимальным, по крайней мере асимптотически. Пусть L (x ₁,…, x_n) - n -мерная плотность выборки, рассматриваемой как один случайный вектор. Для принятой схемы независимых одинаково распределенных наблюдений

.

Если f (x) определена, но содержит неизвестный параметр c (возможно - векторный), то для получения его оценки максимального правдоподобия  предлагается:

1. Подставить в функцию L вместо ее аргументов имеющиеся выборочные значения x ₁,…, x_n, при этом получится функция L (c);
2. Найти значение , при котором L (c) достигает максимума.

Эту процедуру можно применять в самых разнообразных ситуациях, причем (при незначительных добавочных условиях) если при конечных n эффективная оценка существует, то она дается методом максимального правдоподобия.

 

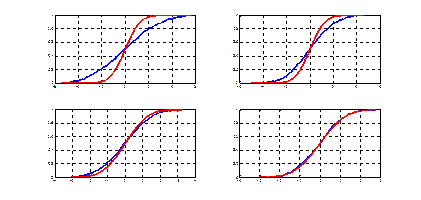
ЛАБОРАТОРНАЯ РАБОТА 1. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА

1. Сформировать матрицу Х < n x m > равномерно-распределённых случайных чисел, n =1000, m =12.
2. Сформировать выборки, представляющие собой суммы 2, 4, 8, 12 столбцов матрицы Х, центрировать и нормировать эти выборки.
3. Построить по этим выборкам эмпирические оценки их функций распределения и привести для сравнения функцию распределения стандартного нормального закона.
4. Построить по этим выборкам эмпирические оценки их плотностей распределения (гистограммы) и привести для сравнения плотность распределения стандартного нормального закона.
5. Прокомментировать полученные результаты с точки зрения центральной предельной теоремы.

 

 

Пример выполнения работы

 

Лабораторная работа 1.

clear; clc; n=1000; m=12; X=rand(m,n)-0.5; M=[2 4 8 12]; F=linspace(0,1,n); for k=1:4; x=sum(X(1:M(k),:)); y=sort(x)*12/M(k); subplot(2,2,k); plot(y,F, 'LineWidth',2); grid; FF=normcdf(y,0,1); hold on; plot(y,FF, 'r', 'LineWidth',2); end; figure; for k=1:4; x=sum(X(1:M(k),:)); y=sort(x)*12/M(k); subplot(2,2,k); q=20; [N,xx]=hist(y,q); del=(y(n)-y(1))/q; N1=N/del/n; bar(xx,N1); grid; FF=normpdf(y,0,1); hold on; plot(y,FF, 'r', 'LineWidth',2); end;

 

Рис. 1.1. Сходимость по распределению к нормальному закону

 

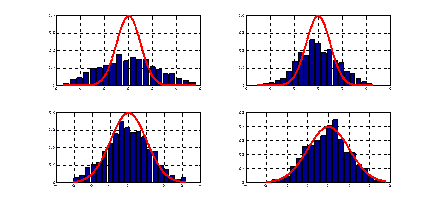
Рис. 1.2. Сходимость оценок плотности к плотности нормального закона

 

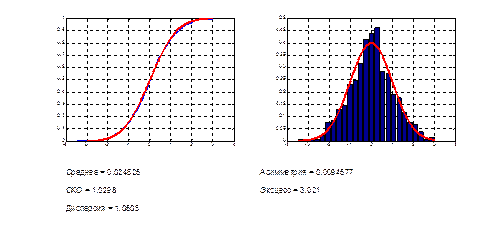
ЛАБОРАТОРНАЯ РАБОТА 2. ТОЧЕЧНОЕ ОЦЕНИВАНИЕ

 

1. Сформировать выборку объёма n из нормального закона N (a, s ²), n =500, оценить среднее, дисперсию, асимметрию, эксцесс.
2. Построить непараметрические оценки функции распределения и плотности, сравнить с теоретическими значениями.
3. Представить все оценки в одном графическом окне.

Пример выполнения работы

 

Лабораторная работа 2.

clear;clc; n=500; a=0; s=1; X=a+s*randn(1,n); F=linspace(0,1,n); X1=sort(X); x=linspace(-3,3,100); a1=mean(X); s1=std(X); D=s1^2; XX=X-a1; AS=mean(XX.^3)/(s1^3); EX=mean(XX.^4)/(s1^4);   q1=[ ' Среднее = ',num2str(a1)]; q2=[ ' СКО = ',num2str(s1)]; q3=[ 'Дисперсия = ',num2str(D)]; q4=[ ' Асимметрия = ',num2str(AS)]; q5=[ ' Эксцесс = ',num2str(EX)];   subplot(3,2,[1 3]); plot(X1,F, 'LineWidth',3); grid; hold on; plot(x,normcdf(x,a,s), 'r', 'LineWidth',3);   subplot(3,2,[2 4]); [N,Z]=hist(X,25); bar(Z,N/(sum(N)*(Z(2)-Z(1)))); grid; hold on; plot(X1,normpdf(X1), 'r', 'LineWidth',3);   subplot(3,2,[5 6]); axis off; text(0,0.8,q1); text(0,0.45,q2); text(0,0.1,q3); text(0.5,0.8,q4); text(0.5,0.45,q5);   %plot(X)

 

 

Рис. 2.1. Оценивание основных характеристик случайной выборки