
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эпсилон-энтропия случайной величиныСодержание книги
Поиск на нашем сайте
Ранее было показано, что неопределенность реализации непрерывным источником информации состояния в конкретный момент времени (отсчёта) равна бесконечности. Тем более равна бесконечности неопределенность реализации непрерывным источником конкретного сигнала длительности Однако такой результата получен в предположении возможности фиксировать любые сколь угодно малые различия между реализациями. На практике такая возможность отсутствует. Это объяснятся тем, что воспринимающие информацию датчики, включая человека, обладают ограниченной чувствительностью и конечной разрешающей способностью, а также тем, что процесс восприятия сопровождается помехами. Если учесть, что нас интересует приближенное восприятие реализации, то количество информации, приходящееся на отсчёт или на единицу времени, можно вычислить. Ограничимся рассмотрением простейшего случая, когда отдельные состояния источника информации представляют собой независимые реализации случайной величины Ансамбль реализаций случайной величины Для количественной оценки степени сходства сигналов целесообразно ввести какую-либо функцию
где Наиболее широко используется среднеквадратический критерий, при котором Требование к верности в данном случае задается с использованием критерия
где Так как плотность
Если случайная величина
может быть записано в форме
где Желательно обеспечить заданную верность воспроизведения при минимальном количестве получаемой информации. Поэтому среди множества функций Минимальное количество информации в одной случайной величине
при
Используя безусловную
где
ИНФОРМАЦИОННЫЕ ХАРАКТЕРИСТИКИ ИСТОЧНИКА СООБЩЕНИЙ И КАНАЛА СВЯЗИ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ Опираясь на формализованное описание сигналов и введенную меру количества информации, рассмотрим информационные характеристики источников сообщений и каналов связи, которые позволяют установить пути повышения эффективности информационных систем, и, в частности, определить условия, при которых можно достигнуть максимальной скорости передачи сообщения по каналу связи как в отсутствие, так и при наличии помех. Источники сообщений и каналы связи в системах передачи отличаются большим разнообразием по своей структуре и физической природе. Используются механические, акустические, оптические, акустические, оптические, электрические и радиоканалы. Для выяснения общих закономерностей необходимо абстрагироваться от их конкретного физического воплощения и оперировать формализованными понятиями источника сообщения и канала связи. Источник дискретных сообщений формирует дискретные последовательности из ограниченного числа элементарных сообщений. На выходе источника непрерывных сообщений образуются непрерывные сообщения. Источник сообщений в теории информации полностью определяется статистическими данными о формируемых им сообщениях.
Под каналом связи подразумевает совокупность устройств и физических сред, которые обеспечивают передачу сообщений из одного места в другое (или от одного момента времени до другого). Если канал используется для передачи дискретных сообщений, он называется дискретным каналом. Непрерывным будем называть канал, предназначенный для передачи непрерывных сообщений. Так как в процессе передачи дискретных сообщений модулятором в соответствии с поступающей последовательностью символов осуществляется изменение информативного параметра непрерывного (чаще всего высокочастотного) сигнала, генерируемого передатчиком в линию связи, то часть дискретного канала от выхода модулятора до входа демодулятора (рис. 43.1) является непрерывным каналом связи. Включив в состав этого канала на передающей стороне модулятор, а на приёмной - демодулятор, получим дискретный канал, характеризуемый на входе, множеством символов Для достижения определенных целей в указанный дискретный канал могут быть введены кодирующие и декодирующие устройства. При этом получаем дискретный канал связи, на вход которого поступают сообщения Рис. 43.1 Если вредным действием помех в канале можно пренебречь, то для анализа используется модель в виде идеализированного канала, называемого каналом без помех. В идеальном канале каждому сообщению на входе однозначно соответствует определенное сообщение на выходе и наоборот. Когда требования к достоверности велики и пренебрежение неоднозначностью связи между сообщениями Канал считается заданным, если известны статистические данные о сообщениях на его входе и выходе и ограничения, накладываемые на входные сообщения физическими характеристиками канала. Канал прямой передачи (от источника сообщений к их получателю), дополненный обратным каналом, например, для запроса повторной передачи в случае обнаружения ошибки, называют каналом с обратной связью.
|
||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.140.96 (0.011 с.) |

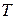 .
.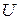 . (Эпсилон-энтропия случайного процесса рассмотрена ниже).
. (Эпсилон-энтропия случайного процесса рассмотрена ниже).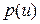 . О значениях случайной величины
. О значениях случайной величины 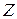 , если мера их различия не превышает заданной верности воспроизведения. В этом случае говорят, что
, если мера их различия не превышает заданной верности воспроизведения. В этом случае говорят, что 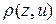 , которая имеет природу "расстояния". Тогда удобным критерием верности
, которая имеет природу "расстояния". Тогда удобным критерием верности 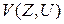 является среднее значение функции
является среднее значение функции 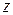 и
и 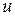 :
: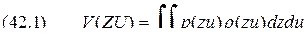 ,
,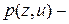 плотность совместного распределения вероятностей величин
плотность совместного распределения вероятностей величин  :
: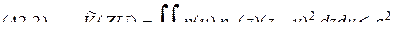 ,
,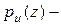 условная плотность распределения – функция правдоподобия того, что конкретный сигнал
условная плотность распределения – функция правдоподобия того, что конкретный сигнал 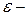 заданное значение верности.
заданное значение верности.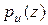 .
.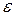 , то количество информации, которое содержится в воспроизводящей величине
, то количество информации, которое содержится в воспроизводящей величине 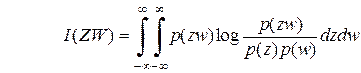 ,
,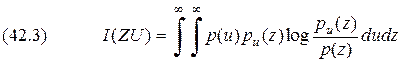 ,
,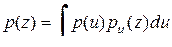 - плотность воспроизводящей величины
- плотность воспроизводящей величины 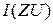 .
.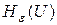 :
: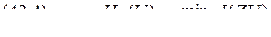
 .
.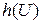 и условную
и условную 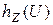 дифференциальные энтропии величины
дифференциальные энтропии величины 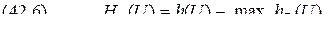 ,
,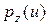 - условная плотность вероятности того, что в тех случаях, когда был принят сигнал
- условная плотность вероятности того, что в тех случаях, когда был принят сигнал  .
.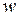 , направляемые адресату. Отметим, что непрерывные сообщения
, направляемые адресату. Отметим, что непрерывные сообщения 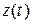 путём дискретизации и квантования всегда можно преобразовать в дискретные и, таким образом, перейти от непрерывно
путём дискретизации и квантования всегда можно преобразовать в дискретные и, таким образом, перейти от непрерывно  го канала к дискретному.
го канала к дискретному.


