
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дискретизация по критерию наибольшего отклонения
В процессе дискретизации непрерывная функция Погрешность восстановления
Следовательно, шаг дискретизации должен быть выбран из условия
Выбор аппроксимирующего многочлена более высокой степени при малой допустимой погрешности В качестве интерполирующего многочлена чаще других используются многочлены Лагранжа, в качестве экстраполирующих – многочлены Тейлора. Дискретизация с использованием интерполирующих многочленов Лагранжа. Интерполирующий многочлен Лагранжа при равномерной дискретизации может быть записан в виде
где Значение остаточного члена
где Дискретизация с использованием экстраполирующих многочленов Тейлора. Экстраполирующий многочлен Тейлора определяется выражением
где Оценка снизу для остаточного члена имеет вид
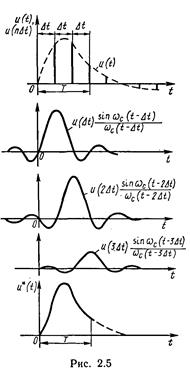
АДАПТИВНАЯ ДИСКРЕТИЗАЦИЯ Если ранее рассмотренные методы и алгоритмы дискретизации были рассчитаны на все множества возможных реализаций сигнала и потому опирались на предельные значений его динамических характеристик, то при адаптивной дискретизации мы ориентируемся на динамические характеристики конкретной реализации, что позволяет получить минимальное число выборок, обеспечивающих восстановление этой реализации с заданной точностью. В основе принципа адаптивной дискретизации лежит непосредственное слежение за текущей погрешностью восстановления сигнала Наиболее широкое применение на практике получили алгоритмы дискретизации с адаптацией по длине интервала аппроксимации. В процессе последовательного наращивания интервала аппроксимации производится сравнение сигнала
В качестве воспроизводящих функций наиболее часто используются степенные алгебраические полиномы нулевой и первой степеней
или где При этом возможны как интерполяционные, так и экстраполяционные способы адаптивной дискретизации. Интерполяционные способы не нашли широкого применения, поскольку их реализация связана с запоминанием сигнала на интервале аппроксимации м выполнением большого числа вычислительных операций. КВАНТОВАНИЕ СИГНАЛА Так как математической моделью непрерывного сигнала является случайный процесс сигнала разбивают на постоянна на всём протяжении непрерывной шкалы мгновенных значений сигнала
В результате замены мгновенного значений сигнала которую называют ошибкой квантования. Эта погрешность является случайной величиной. Но чаще всего интересует её максимальное значение и среднеквадратическое отклонение
С позиций минимизации наибольшей возможной ошибки квантования непрерывную шкалу мгновенных значений сигнала целесообразно разбить на
и уровни квантования разместить в середине каждого шага. при этом максимальная ошибка квантования не превышает
Рис. Среднеквадратическое отклонение ошибки квантования для
где Считая шаги квантования малыми по сравнению с диапазоном изменения сигнала, плотности
Преобразовав подкоренное выражение к виду
отметим, что дисперсия ошибки квантования на
При одинаковых шагах квантования
Так как принимаем
то
Таким образом, при квантовании с постоянным шагом и размещением уровней квантования в середине шага (равномерное квантование) среднеквадратическая ошибка квантования как для равномерного, так и произвольного распределения мгновенных значений сигнала одинакова:
Шум квантования. При квантовании сигнала по уровню случайный процесс заменяется ступенчатой зависимостью
Сохраняя ранее введенные предположения (о малости шага квантования и равномерности распределения в нём мгновенных значений сигнала) и считая случайные процессы
Так как
При заданной допустимой среднеквадратической ошибке квантовании и отсутствии помех число уровней квантования находим из соотношения
Однако при неравномерном законе распределение мгновенных значений сигнала квантование с постоянным шагом не является оптимальным по критерию минимума среднеквадратической ошибки
|
||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.103.202 (0.023 с.) |
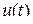 , которая имеет
, которая имеет 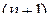 ограниченных производных, аппроксимируется многочленом
ограниченных производных, аппроксимируется многочленом 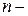 й степени. В зависимости от выбранного способа восстановления он может быть аппроксимирующим или экстраполирующим. Задача обеспечения минимальной погрешности при восстановлении сигнала на практике не ставится. Обычно указывается её допустимое значение
й степени. В зависимости от выбранного способа восстановления он может быть аппроксимирующим или экстраполирующим. Задача обеспечения минимальной погрешности при восстановлении сигнала на практике не ставится. Обычно указывается её допустимое значение 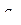 .
.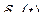 функции
функции  на каждом участке аппроксимации определяется остаточным членом
на каждом участке аппроксимации определяется остаточным членом 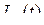
 .
.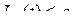 .
.

 ,
, ,
,  ,
, 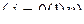 .
.
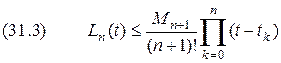 ,
,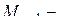 максимальный во всём интервале преобразования модуль
максимальный во всём интервале преобразования модуль 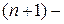 производной сигнала
производной сигнала  ,
,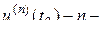 я производная сигнала
я производная сигнала 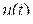 в момент времени
в момент времени  .
.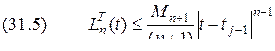 ,
, 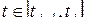 .
.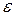 .
.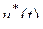 , формируемой с учётом текущих значений динамических характеристик сигнала. Когда погрешность воспроизведения достигает заданного значения
, формируемой с учётом текущих значений динамических характеристик сигнала. Когда погрешность воспроизведения достигает заданного значения 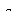 , наращивание интервала прекращается и производится отсчёт. Интервалы времени между отсчётами при этом оказываются произвольными.
, наращивание интервала прекращается и производится отсчёт. Интервалы времени между отсчётами при этом оказываются произвольными.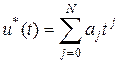
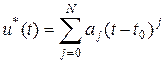 ,
,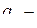 действительные коэффициенты.
действительные коэффициенты.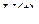 , мгновенное значение сигнала
, мгновенное значение сигнала 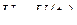 представляет собой случайную величину. Диапазон её изменения, называемый непрерывной шкалой мгновенных значений сигнала ограничен значениями
представляет собой случайную величину. Диапазон её изменения, называемый непрерывной шкалой мгновенных значений сигнала ограничен значениями 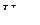 и
и 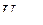 , что отражает условие физической реализуемости сигнала. Непрерывную шкалу мгновенных значений
, что отражает условие физической реализуемости сигнала. Непрерывную шкалу мгновенных значений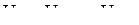
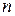 интервалов, которые называют шагами квантования. Границами шагов квантования являются значения
интервалов, которые называют шагами квантования. Границами шагов квантования являются значения 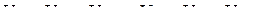 . Из множества мгновенных значений, которые принадлежат
. Из множества мгновенных значений, которые принадлежат  му шагу квантования
му шагу квантования 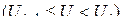 , только одно значение
, только одно значение 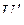 является разрешенным (
является разрешенным (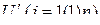 образует дискретную шкалу уровней квантования. Если эта шкала равномерная, т.е. разности значений
образует дискретную шкалу уровней квантования. Если эта шкала равномерная, т.е. разности значений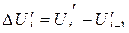
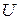 , квантование называют равномерным. Если постоянство значений
, квантование называют равномерным. Если постоянство значений 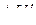 не выдерживается – квантование неравномерное. Благодаря простоте технической реализации равномерное квантование получило наиболее широкое распространение.
не выдерживается – квантование неравномерное. Благодаря простоте технической реализации равномерное квантование получило наиболее широкое распространение.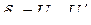 ,
,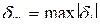
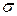 от всего диапазона изменения мгновенных значений сигнала. Используются также приведенные значения этих величин
от всего диапазона изменения мгновенных значений сигнала. Используются также приведенные значения этих величин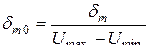 ,
,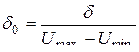 .
.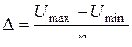
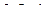 . Если каждый уровень квантования выбран равным нижней (верхней) границе шага квантования, максимальная ошибка квантования возрастает до величины
. Если каждый уровень квантования выбран равным нижней (верхней) границе шага квантования, максимальная ошибка квантования возрастает до величины 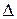 .
.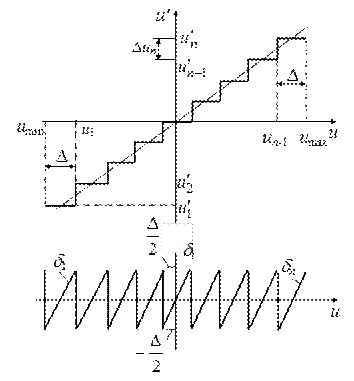
 зависит не только от шага
зависит не только от шага 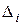 и расположения в нём
и расположения в нём 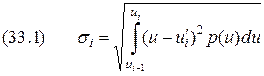 ,
,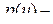 функция плотности вероятности мгновенных значений сигнала
функция плотности вероятности мгновенных значений сигнала 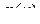 в пределах каждого
в пределах каждого 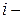 го шага можно принять постоянной и равной некоторому среднему значению, например
го шага можно принять постоянной и равной некоторому среднему значению, например 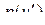 . При таких предположениях минимальная среднеквадратическая ошибка
. При таких предположениях минимальная среднеквадратическая ошибка 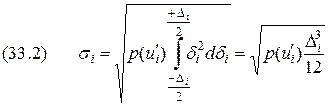 .
.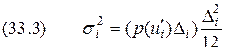 ,
,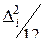 равномерно распределенного на этом шаге сигнала, умноженной на вероятность
равномерно распределенного на этом шаге сигнала, умноженной на вероятность 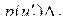 попадания мгновенного значений сигнала в пределы данного шага. Дисперсия полной ошибки квантования
попадания мгновенного значений сигнала в пределы данного шага. Дисперсия полной ошибки квантования 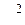 для всей непрерывной шкалы мгновенных значений сигнала определяется как математическое ожидание дисперсий
для всей непрерывной шкалы мгновенных значений сигнала определяется как математическое ожидание дисперсий 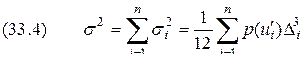 .
.
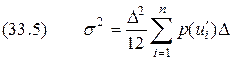 .
.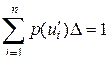 ,
,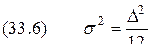 .
.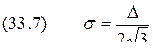 .
. . Ошибку квантования
. Ошибку квантования  , которая изменяется во времени и также представляет собой случайный процесс, называют шумом квантования:
, которая изменяется во времени и также представляет собой случайный процесс, называют шумом квантования: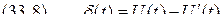 .
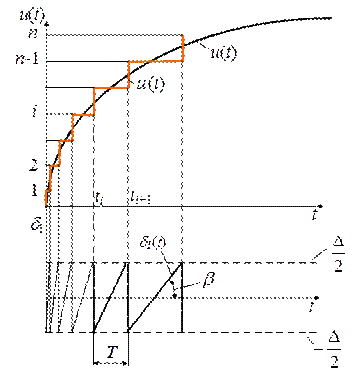
.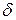 можно определить по реализации
можно определить по реализации 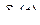 (рис.). В пределах каждого квантования
(рис.). В пределах каждого квантования 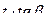 , где
, где 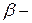 переменный угол наклона прямой. При размещении уровней квантования в середине каждого шага математическое ожидание ошибки равно нулю, а её среднеквадратическое значение определяется выражением
переменный угол наклона прямой. При размещении уровней квантования в середине каждого шага математическое ожидание ошибки равно нулю, а её среднеквадратическое значение определяется выражением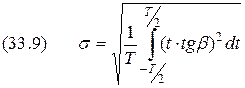 .
.
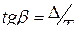 , то
, то 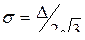 , что соответствует ранее полученному значению (см. выражение (33.7)).
, что соответствует ранее полученному значению (см. выражение (33.7)).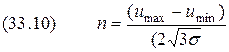 .
.


