Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотная форма представления сигнала. Спектры непериодических сигналов
Любой физически реализуемый сигнал ограничен во времени и обладает конечной энергией. Функции, которые отображают реальные сигналы, удовлетворяют условиям Дирихле и абсолютно интегрируемы, т.е.
где Модели таких сигналов также могут представлены совокупностью гармонических составляющих в соответствии с выражением (8.2) Конкретный вид спектрального преобразования для непериодического сигнала получим, проследив изменения, которые происходят в спектре периодической последовательности Приведём без вывода выражение, которое определяет спектр амплитуд периодической последовательности импульсов
Здесь
при увеличении периода уменьшаются. Так как частоты составляющих спектра кратны основной частоте, то при её уменьшении линии на спектральной диаграмме сближаются. Спектральные представления для одиночного импульса Пару преобразований Фурье для периодической функции
При
Обозначив интеграл в скобках как
Величину
и (13.3), находим, что бесконечно малому интервалу частоты
Сравнение выражение (13.2) для спектральной характеристики функции показывает, что они различаются только множителем
Поэтому по известной спектральной характеристике одиночного импульса можно построить линейчатый спектр в их периодической последовательности. Соотношением (13.5) объясняется и тот факт, что для различных представлений спектральной характеристики имеют место формулы, весьма похожие на (11.5) - (11.11). Как комплексная величина спектральная характеристика может быть записана в виде
где Так как составляющие расположены на всех частотах, то спектр непериодического сигнала является непрерывным или сплошным. Представим спектральную характеристику состоящей из действительной и мнимой частей
где
Модуль спектральной характеристики
и представляет собой четную функцию частоты. Для спектральной характеристики
Так как из (13.7) и (13.8) следует, что Комплексная форма интегрального преобразования Фурье приводится к тригонометрической
Второй член в связи с нечетностью подынтегрального выражения равен нулю. Окончательно имеем
Преимущество тригонометрической формы записи Фурье-преобразования заключается в возможности некоторого физического толкования с использованием идеализаций, не очень далеких от реальности.
|
|||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.22.169 (0.011 с.) |

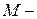 конечная величина.
конечная величина.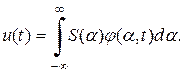
 при увеличении периода их повторения.
при увеличении периода их повторения.
 - амплитуда импульсов;
- амплитуда импульсов;  - период повторения импульсов;
- период повторения импульсов;  - длительность импульсов;
- длительность импульсов; 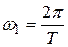 - частота повторения импульсов. Абсолютные значения амплитуд спектральных составляющих в (11.4), т.е.
- частота повторения импульсов. Абсолютные значения амплитуд спектральных составляющих в (11.4), т.е.
 получим как следствие увеличения периода сигнала
получим как следствие увеличения периода сигнала  запишем в форме
запишем в форме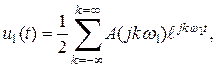

 импульс
импульс 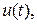 частота
частота  уменьшается до
уменьшается до 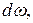 а
а 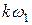 превращается в текущую частоту
превращается в текущую частоту 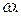 Заменяя суммирование интегрированием, находим
Заменяя суммирование интегрированием, находим
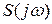 , получим формулы для прямого и обратного преобразования Фурье
, получим формулы для прямого и обратного преобразования Фурье
 (13.3)
(13.3)
 соответствует составляющая с бесконечно малой комплексной амплитудой
соответствует составляющая с бесконечно малой комплексной амплитудой 
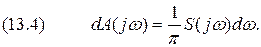
 заданной на интервале времени
заданной на интервале времени  с формулой (11.4) для огибающей комплексного спектра такой же функции, периодически продолжающейся во времени, т.е.
с формулой (11.4) для огибающей комплексного спектра такой же функции, периодически продолжающейся во времени, т.е. ,
,

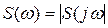 - называется спектральной плотностью амплитуд или спектром непериодического сигнала, аргумент спектральной характеристики, взятый с обратным знаком, называется фазовым спектром. С учётом последнего запишем
- называется спектральной плотностью амплитуд или спектром непериодического сигнала, аргумент спектральной характеристики, взятый с обратным знаком, называется фазовым спектром. С учётом последнего запишем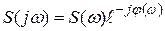 .
.

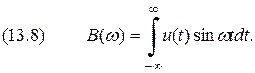
 определяется выражением
определяется выражением
 соответственно получаем
соответственно получаем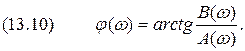
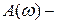 четная функция частоты, а
четная функция частоты, а  нечетная, то функция
нечетная, то функция  относительно частоты нечетна.
относительно частоты нечетна.