
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уровни проблем передачи информацииСодержание книги
Поиск на нашем сайте
ЭТАПЫ ОБРАЩЕНИЯ ИНФОРМАЦИИ Отметим роль (цель) информации - неопределенное эмоциональное воздействие на человека. В автоматических и автоматизированных системах информация чаще всего используется для выработки управляющих воздействий. При обращении (циркуляции, обороте) информации в таких системах можно выделить следующие этапы, и так как материальным носителем информации является сигнал, то реально это будут этапы обращения и преобразования сигналов. На этапе восприятия информации осуществляется целенаправленное извлечение и анализ информации о каком-либо объекте (процессе), в результате чего формируется образ объекта, проводятся его распознавание (опознавание) и оценка. При этом необходимо отделить ту информацию (полезная информация), которая интересует нас в данном случае, от информации, которая мешает нам правильно воспринимать необходимую. Мешающая информация - это помехи, шумы, сбои и т. п. Отметим, что в ряде случаев выделение полезной информации на фоне помех представляет не простую задачу. Простейшим видом восприятия является определение двух противоположных состояний: наличие ("да") и отсутствие ("нет"), более сложным - измерение. На этапе подготовки информации проводятся такие операции, как нормализация, аналого-цифровое преобразование, шифрование. Иногда этот этап рассматривается как вспомогательный на этапе восприятия. В результате восприятия и подготовки получается сигнал в форме, удобной для передачи и обработки. На этапах передачи и хранения информация пересылается либо из одного места в другое, либо от одного момента времени до другого. Поскольку теоретические задачи, возникающие на этих этапах близки друг к другу, этап хранения информации обычно в самостоятельный этап не выделяется. При этом термин передача информации получает более широкое толкование. Для передачи на расстояние используются каналы различной физической природы, самыми распространенными из которых являются электрические и электромагнитные. Для хранения информации используются в основном полупроводниковые и магнитные носители. Извлечение сигнала на выходе канала, подверженного действию шумов, носит характер вторичного восприятия.
На этапах обработки информации выявляются её общие и существенные взаимозависимости, которые представляют интерес для системы. Преобразование информации на этапе обработки (как и на других этапах) осуществляется либо техническими средствами, либо человеком. В настоящее время технические средства это в большинстве своём средства вычислительной техники, которые применимы в тех случаях, если процесс обработки информации формализован. Если же процесс обработки не поддается формализации и требует творческого подхода, обработка информации осуществляется человеком. В системах управления важнейшей целью обработки является решение задачи выбора управляющих воздействий (этап принятия решения). Этап отображения информации должен предшествовать этапу, связанным с участием человека. Цель этапа отображения - предоставить человеку нужную ему информацию с помощью устройств, которые способны воздействовать на его органы чувств. На этапе воздействия информация используется для осуществления необходимых изменений в системе.
ИНФОРМАЦИОННЫЕ СИСТЕМЫ Совокупность средств информационной техники и людей, объединенных для достижения определенных целей, образует автоматизированную информационную систему, к которой по мере надобности подключаются абоненты (люди или устройства), которые поставляют и используют информацию. Информационные системы, которые действуют без участия человека, называются автоматическими. За человеком в таких системах остаются функции контроля и обслуживания. Автоматизированная информационная система становится автоматизированной системой управления (АСУ), если поставляемая информация извлекается из какого-либо объекта (процесса), а выходная используется для целенаправленного изменения состояния того же объекта (процесса), причем абонентом, использующим информацию для выбора основных управляющих воздействий (принятия решения), является человек. Объектом могут быть техническая система, экологическая среда, коллектив людей. Известны и такие АСУ, в которых отдельные функции управления возлагаются на технические средства, в основном на ЭВМ и микропроцессоры. Автоматизированные информационные системы и АСУ нашли широкое применение во всех отраслях экономики в первую очередь как информационно-справочные и информационно-советующие системы, системы управления технологическими процессами и коллективами людей. До недавнего времени большинство из них являлись локальными системами и функционировали на уровне предприятий и учреждений. В настоящее время происходит интенсивный процесс интеграции таких систем.
Системы более высокого уровня становятся территориально рассредоточенными, иерархичными как по функциональному принципу, так и по реализации их техническими средствами. Обеспечение взаимодействия территориально рассредоточенных систем требует протяженных высокоскоростных и надежных каналов связи, а увеличение объема обрабатываемой информации – средств вычислительной техники высокой производительности. Это привело к необходимости коллективного использования дорогостоящих средств автоматизации (средств вычислительной техники и линий связи) и обрабатываемой информации (банков и баз данных). Централизация различных видов информации в одной сети дает возможность использовать её для решения широкого спектра задач, связанных с административным управлением, планированием, научными исследованиями, конструкторскими разработками, технологией производства, снабжением, учетом и отчетностью. Наиболее распространенными информационными системами являются системы, которые обеспечивают передачу информации из одного места в другое (системы связи) и от одного момента времени до другого (системы хранения информации). Обе разновидности систем передачи информации имеют много общего в принципиальных вопросах обеспечения эффективности функционирования. Их применяют как самостоятельные системы и как подсистемы в составе любых более сложных информационных систем. Совокупность таких подсистем в информационно-вычислительной сети образует её основное ядро - сеть передачи данных.
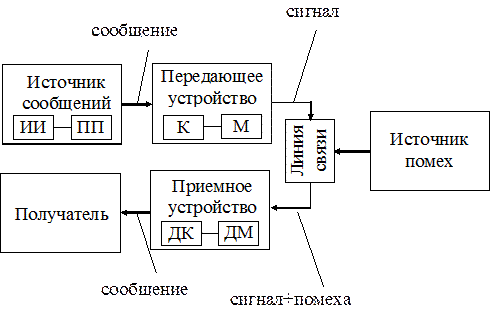
4. СИСТЕМА ПЕРЕДАЧИ ИНФОРМАЦИИ: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ Функциональная схема одноканальной системы передачи информации приведена на рис. 4.1. Информация поступает в систему в форме сообщений. Под сообщением понимают совокупность знаков или первичных сигналов, которые содержат информацию. Источник сообщений в общем случае образует совокупность источника информации ИИ (исследуемого или наблюдаемого объекта) и первичного преобразователя ПП (датчика, человека-оператора и т. п.), который воспринимает информацию о его состояниях или протекающем в нем процессе. Различают дискретные и непрерывные сообщения. Дискретные сообщения формируются в результате последовательной выдачи источником отдельных элементов - знаков. Множество различных знаков называют алфавитом источника сообщений, а число знаков - объемом алфавита. В частности, знаками могут быть буквы естественного или искусственного языка, которые удовлетворяют определенным правилам взаимосвязи. Распространенной разновидностью дискретных сообщений являются данные. Непрерывные сообщения не разделимы на элементы. Они описываются функциями времени, принимающими непрерывное множество значений. Типичными примерами непрерывных сообщений могут служить речь, телевизионные изображения. В ряде информационных систем непрерывные сообщения с целью повышения качества передачи преобразуются в дискретные.
Рис. 4.1
Для передачи по каналу связи сообщения ему необходимо поставить в соответствие определенный сигнал. В информационных системах под сигналом понимают физический процесс, отображающий (несущий) сообщение. Преобразование сообщения в сигнал, удобный для передачи по данному каналу связи, называют кодированием в широком смысле слова. Операцию восстановления сообщения по принятому сигналу называют декодированием. Так как число возможных дискретных сообщений при неограниченном увеличении времени стремится к бесконечности, а за достаточно большой промежуток времени весьма велико, то ясно, что создать для каждого сообщения свой сигнал практически невозможно. Однако, поскольку дискретные сообщения складываются из знаков, имеется возможность обойтись конечным числом образцовых сигналов, которые соответствуют отдельным знакам алфавита источника. Для обеспечения простоты и надежности распознавания образцовых сигналов их число целесообразно сократить до минимума. Поэтому, как правило, прибегают к операции представления исходных знаков в другом алфавите с меньшим числом знаков, называемых символами. При обозначении этой операции используется тот же термин "кодирование", который рассматривается в узком смысле. Устройство, которое выполняет такую операцию, называют кодирующим или кодером К. Так как алфавит символов меньше алфавита знаков, то каждому знаку соответствует некоторая последовательность символов, которую назовем кодовой комбинацией. Число символов в кодовой комбинации называют её значностью, число ненулевых символов - весом. Аналогично, для операции сопоставления символов со знаками исходного алфавита используется термин "декодирование". Техническая реализация её осуществляется декодирующим устройством или декодером ДК. В простейшей системе связи кодирующее, а следовательно, и декодирующее устройство может отсутствовать. Передающее устройство осуществляет преобразование непрерывных сообщений или знаков в сигналы, удобные для прохождения по конкретной линии связи (либо для хранения в некотором запоминающем устройстве). При этом один или несколько параметров выбранного носителя изменяют в соответствии с передаваемой информацией. Такой процесс называют модуляцией. Он осуществляется модулятором М. Обратное преобразование сигналов в символы производится демодулятором ДМ. Под линией связи понимают любую физическую среду (воздух, металл, магнитную ленту, магнитный диск и т. п.), которая обеспечивает поступление сигналов от передающего устройства к приемному. Сигналы на выходе линии связи могут отличаться от переданных вследствие затухания, искажения и воздействия помех. Помехами называют любые мешающие возмущения, как внешние (атмосферные помехи, промышленные помехи), так и внутренние (источником которых являются сами аппаратные средства информационных систем), вызывающие случайные отклонения принятых сигналов от переданных. Эффект воздействия помех на различные блоки системы стараются учесть эквивалентным изменением характеристик линии связи. Поэтому источник помех условно относят к линии связи.
Из смеси сигнала и помехи приемное устройство выделяет сигнал и посредством декодера восстанавливает сообщение, которое в общем случае может отличаться от посланного. Меру соответствия принятого сообщения посланному называют верностью передачи. Обеспечение заданной верности передачи сообщений - важнейшая цель системы связи. Принятое сообщение с выхода системы связи поступает к абоненту-получателю, которому была адресована исходная информация. Совокупность средств, предназначенных для передачи сообщений, называют каналом связи. Для передачи информации от группы источников, которые сосредоточены в одном пункте, к группе получателей, расположенных в другом пункте, часто целесообразно использовать только одну линию связи, организовав на ней требуемое число каналов. Такие системы называют многоканальными.
ТЕОРИЯ ИНФОРМАЦИИ Как уже отмечалось выше для того, чтобы проанализировать смысл высказываний, или оценить эффект, ими произведенный, необходима некоторая система знаков, составляющая например, естественный или искусственный язык. Данная система знаков имеет свои внутренние свойства, которые составляют синтаксическую часть информации. Именно эта часть информации изучается в математической дисциплине, которая и именуется как "Теория информации". Здесь полностью абстрагируются от смысла и эффекта информации и основное внимание уделяют вопросам измерения её количества, фундаментальных границах для её сжатия и надёжной передачи. Если в физике давно научились измерять количество материи и энергии, то о том же, как измерить количество информации, мы знаем только с 1948 г., когда появилась статья Клода Шеннона "A Mathematical Theory of Communication", название которой при переиздании в виде книги год спустя было изменено на "The Mathematical Theory of Communication". То есть Шеннон к этому времени понял, что его результаты в теории информации имеют фундаментальное значение для передачи сообщений (коммуникации). Однако в научном мире эти результаты были крайне новыми, а идеи необычными, поэтому потребовались годы для их осознания. И только через 35-40 лет фундаментальные достижения теории информации, в которую органически вошли и результаты, полученные другими учеными, например Р. Хартли, который впервые предложил в 1928 году количественную меру информации были включены в повседневное использование.
К теории информации в её узкой классической постановке относят результаты решения ряда фундаментальных теоретических вопросов, которые касаются повышения эффективности функционирования систем связи. Это в первую очередь: анализ сигналов как средства передачи сообщений, который включает вопросы оценки переносимого ими "количества информации"; анализ информационных характеристик источников сообщений и каналов связи и обоснование принципиальной возможности кодирования и декодирования сообщения, которые обеспечивают предельно допустимую скорость передачи сообщений по каналу связи как при отсутствии, так и при наличии помех. Прикладные результаты приводятся здесь только для пояснения основ теории. При более широкой трактовке теории информации результаты рассмотрения указанных вопросов составляют её основу, при этом расширяя и углубляя их. Так если, рассмотрение связано с приложением теории информации в технике связи - рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации. Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации информационных систем в целом. В этом случае к ней относят все локальные проблемы информационных систем, включая, например, проблему оптимального приема и др. В соответствии с третьей крайней точкой зрения к компетенции теории информации относят все проблемы и задачи, в формулировку которых входит понятие информации. Её предметом считают изучение процессов, связанных с получением, передачей, хранением, обработкой и использованием информации. В такой постановке она затрагивает проблемы многих наук (в частности, кибернетики, биологии, психологии, лингвистики, педагогики) на всех трех уровнях: синтаксическом, семантическом и прагматическом. Попытки широкого использования идей теории информации в различных областях науки связаны с тем, что в основе своей эта теория математическая. Основные её понятия (энтропия, количество информации, пропускная способность) определяются только через вероятности событий, которым может быть приписано самое различное физическое содержание. Подход к исследованиям в других областях науки с позиции использования основных идей теории информации получил название теоретико-информационного подхода. Его применение в ряде случаев позволило получить новые теоретические результаты и ценные практические рекомендации. Однако нередко такой подход приводит к созданию моделей процессов, далеко не адекватных реальной действительности. Поэтому в любых исследованиях, выходящих за рамки чисто технических проблем передачи и хранения сообщений, теорией информации следует пользоваться с большой осторожностью. Особенно это касается моделирования умственной деятельности человека, процессов восприятия и обработки им информации.
И ШИРИНОЙ ИХ СПЕКТРА Анализируя спектр одиночного прямоугольного импульса, можно установить, что при увеличении его длительности Рассмотрим функцию
где Следовательно, спектр укороченного в Другой важный вывод, который также является прямым следствием Фурье-преобразования, заключается в том, что длительность сигнала и ширина его спектра не могут быть одновременно ограничены конечными интервалами, и, наоборот, сигнал с ограниченным спектром длится бесконечно долго. Справедливо соотношение
где Реальные сигналы ограничены во времени, генерируются и передаются устройствами, которые содержат инерционные элементы (например, емкости и индуктивности в электрических цепях), и поэтому не могут содержать гармонические составляющие сколь угодно высоких частот. В связи с этим возникает необходимость ввести в рассмотрение модели сигналов, которые обладают как конечной длительностью, так и ограниченным спектром. При этом в соответствии с каким-либо критерием дополнительно ограничивается либо ширина спектра, либо длительность сигнала, либо оба параметра одновременно. В качестве такого критерия используется энергетический критерий, согласно которому практическую длительность Для сигналов, которые начинаются в момент времени
где Принимая во внимание равенство Парсеваля при практической ширине спектра сигнала соответственно имеем
СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ АДАПТИВНАЯ ДИСКРЕТИЗАЦИЯ Если ранее рассмотренные методы и алгоритмы дискретизации были рассчитаны на все множества возможных реализаций сигнала и потому опирались на предельные значений его динамических характеристик, то при адаптивной дискретизации мы ориентируемся на динамические характеристики конкретной реализации, что позволяет получить минимальное число выборок, обеспечивающих восстановление этой реализации с заданной точностью. В основе принципа адаптивной дискретизации лежит непосредственное слежение за текущей погрешностью восстановления сигнала Наиболее широкое применение на практике получили алгоритмы дискретизации с адаптацией по длине интервала аппроксимации. В процессе последовательного наращивания интервала аппроксимации производится сравнение сигнала В качестве воспроизводящих функций наиболее часто используются степенные алгебраические полиномы нулевой и первой степеней
или где При этом возможны как интерполяционные, так и экстраполяционные способы адаптивной дискретизации. Интерполяционные способы не нашли широкого применения, поскольку их реализация связана с запоминанием сигнала на интервале аппроксимации м выполнением большого числа вычислительных операций. КВАНТОВАНИЕ СИГНАЛА Так как математической моделью непрерывного сигнала является случайный процесс сигнала разбивают на постоянна на всём протяжении непрерывной шкалы мгновенных значений сигнала В результате замены мгновенного значений сигнала которую называют ошибкой квантования. Эта погрешность является случайной величиной. Но чаще всего интересует её максимальное значение и среднеквадратическое отклонение
С позиций минимизации наибольшей возможной ошибки квантования непрерывную шкалу мгновенных значений сигнала целесообразно разбить на
и уровни квантования разместить в середине каждого шага. при этом максимальная ошибка квантования не превышает
Рис. Среднеквадратическое отклонение ошибки квантования для
где Считая шаги квантования малыми по сравнению с диапазоном изменения сигнала, плотности
Преобразовав подкоренное выражение к виду
отметим, что дисперсия ошибки квантования на
При одинаковых шагах квантования
Так как принимаем
то
Таким образом, при квантовании с постоянным шагом и размещением уровней квантования в середине шага (равномерное квантование) среднеквадратическая ошибка квантования как для равномерного, так и произвольного распределения мгновенных значений сигнала одинакова:
Шум квантования. При квантовании сигнала по уровню случайный процесс заменяется ступенчатой зависимостью
Сохраняя ранее введенные предположения (о малости шага квантования и равномерности распределения в нём мгновенных значений сигнала) и считая случайные процессы
Так как При заданной допустимой среднеквадратической ошибке квантовании и отсутствии помех число уровней квантования находим из соотношения
Однако при неравномерном законе распределение мгновенных значений сигнала квантование с постоянным шагом не является оптимальным по критерию минимума среднеквадратической ошибки СВОЙСТВА ЭНТРОПИИ Рассмотрим основные свойства энтропии, обратив внимание на то, что сформулированные условия для меры неопределенности выполняются. 1.Энтропия является вещественной и неотрицательной величиной, так как для любого 2.Энтропия – величина ограниченная. Для слагаемых
Обозначив
3.Энтропия обращается в нуль лишь в том случае, если вероятность одного из состояний равна единице; тогда вероятности всех остальных состояний, естественно равны нулю. Это положение соответствует случаю, когда состояние источника полностью определенно. 4.Энтропия максимальна, когда все состояния равновероятны, что можно доказать методом неопределенных множителей Лагранжа:
5.Энтропия источника
График зависимости
Отметим, что энтропия непрерывно зависит от вероятностей отдельных состояний, что непосредственно вытекает из непрерывности функции 6.Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропий исходных источников. Не теряя общности, ограничимся рассмотрением объединения, которое включает два источника информации В соответствии с определением энтропия объединения
Здесь В случае статистической независимости источников информации Тогда
Учитывая, что
получим
Соответственно для энтропии объединения нескольких независимых источников
В дальнейшем для придания общности получаемым результатам о неопределенности выбора б
|
|||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.170.80 (0.016 с.) |

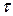 от
от 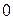 до
до 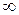 спектр сокращается от безграничного (дельта-функция) до одной спектральной линии в начале координат, которая соответствует постоянному значению сигнала. Это свойство сокращения ширины спектра сигнала при увеличении его длительности и наоборот справедливо для сигналов любой формы. Оно вытекает непосредственно из особенностей прямого и обратного интегрального преобразования Фурье, у которых показатель степени экспоненциальной функции в подынтегральных выражениях имеет переменные
спектр сокращается от безграничного (дельта-функция) до одной спектральной линии в начале координат, которая соответствует постоянному значению сигнала. Это свойство сокращения ширины спектра сигнала при увеличении его длительности и наоборот справедливо для сигналов любой формы. Оно вытекает непосредственно из особенностей прямого и обратного интегрального преобразования Фурье, у которых показатель степени экспоненциальной функции в подынтегральных выражениях имеет переменные 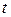 и
и 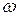 в виде произведения.
в виде произведения.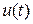 определённой длительности и функцию
определённой длительности и функцию 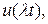 длительность которой при
длительность которой при 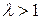 будет в
будет в 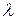 раз меньше. Считая, что
раз меньше. Считая, что 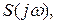 найдем соответствующую характеристику
найдем соответствующую характеристику 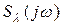 для
для 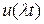 :
: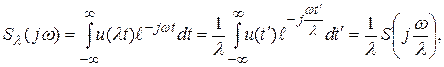 (15.1)
(15.1)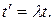
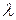 раз шире. Коэффициент
раз шире. Коэффициент 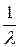 перед
перед 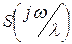 изменяет только амплитуду гармонических составляющих и на ширину спектра не влияет.
изменяет только амплитуду гармонических составляющих и на ширину спектра не влияет.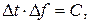 (15.2)
(15.2)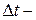 длительность импульса;
длительность импульса; 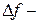 ширина спектра импульса;
ширина спектра импульса; 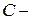 постоянная величина, зависящая от формы импульса (при ориентировочных оценках обычно принимают
постоянная величина, зависящая от формы импульса (при ориентировочных оценках обычно принимают 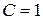 ).
).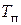 и практическую ширину спектра
и практическую ширину спектра 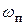 выбирают так, чтобы в них была сосредоточена подавляющая часть энергии сигнала.
выбирают так, чтобы в них была сосредоточена подавляющая часть энергии сигнала.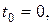 практическая длительность определяется из соотношения
практическая длительность определяется из соотношения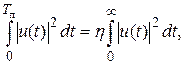 (15.3)
(15.3)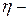 коэффициент, достаточно близкий к 1 (от 0,9 до 0,99 в зависимости от требований к качеству воспроизведения сигнала).
коэффициент, достаточно близкий к 1 (от 0,9 до 0,99 в зависимости от требований к качеству воспроизведения сигнала).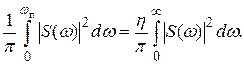 (15.4)
(15.4)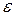 .
.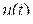 с воспроизводящей функцией
с воспроизводящей функцией 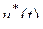 , формируемой с учётом текущих значений динамических характеристик сигнала. Когда погрешность воспроизведения достигает заданного значения
, формируемой с учётом текущих значений динамических характеристик сигнала. Когда погрешность воспроизведения достигает заданного значения 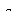 , наращивание интервала прекращается и производится отсчёт. Интервалы времени между отсчётами при этом оказываются произвольными.
, наращивание интервала прекращается и производится отсчёт. Интервалы времени между отсчётами при этом оказываются произвольными.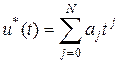
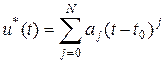 ,
,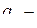 действительные коэффициенты.
действительные коэффициенты.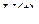 , мгновенное значение сигнала
, мгновенное значение сигнала 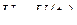 представляет собой случайную величину. Диапазон её изменения, называемый непрерывной шкалой мгновенных значений сигнала ограничен значениями
представляет собой случайную величину. Диапазон её изменения, называемый непрерывной шкалой мгновенных значений сигнала ограничен значениями 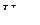 и
и 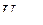 , что отражает условие физической реализуемости сигнала. Непрерывную шкалу мгновенных значений
, что отражает условие физической реализуемости сигнала. Непрерывную шкалу мгновенных значений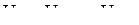
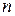 интервалов, которые называют шагами квантования. Границами шагов квантования являются значения
интервалов, которые называют шагами квантования. Границами шагов квантования являются значения 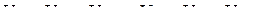 . Из множества мгновенных значений, которые принадлежат
. Из множества мгновенных значений, которые принадлежат  му шагу квантования
му шагу квантования 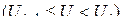 , только одно значение
, только одно значение 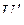 является разрешенным (
является разрешенным (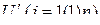 образует дискретную шкалу уровней квантования. Если эта шкала равномерная, т.е. разности значений
образует дискретную шкалу уровней квантования. Если эта шкала равномерная, т.е. разности значений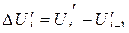
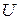 , квантование называют равномерным. Если постоянство значений
, квантование называют равномерным. Если постоянство значений 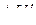 не выдерживается – квантование неравномерное. Благодаря простоте технической реализации равномерное квантование получило наиболее широкое распространение.
не выдерживается – квантование неравномерное. Благодаря простоте технической реализации равномерное квантование получило наиболее широкое распространение.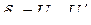 ,
,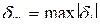
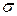 от всего диапазона изменения мгновенных значений сигнала. Используются также приведенные значения этих величин
от всего диапазона изменения мгновенных значений сигнала. Используются также приведенные значения этих величин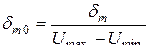 ,
,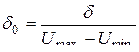 .
.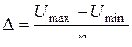
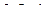 . Если каждый уровень квантования выбран равным нижней (верхней) границе шага квантования, максимальная ошибка квантования возрастает до величины
. Если каждый уровень квантования выбран равным нижней (верхней) границе шага квантования, максимальная ошибка квантования возрастает до величины 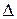 .
.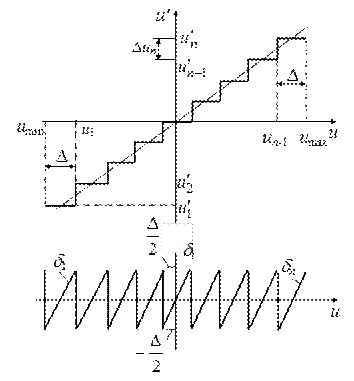
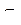 зависит не только от шага
зависит не только от шага 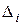 и расположения в нём
и расположения в нём 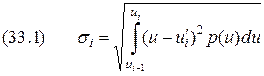 ,
,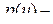 функция плотности вероятности мгновенных значений сигнала
функция плотности вероятности мгновенных значений сигнала 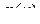 в пределах каждого
в пределах каждого 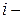 го шага можно принять постоянной и равной некоторому среднему значению, например
го шага можно принять постоянной и равной некоторому среднему значению, например 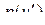 . При таких предположениях минимальная среднеквадратическая ошибка
. При таких предположениях минимальная среднеквадратическая ошибка 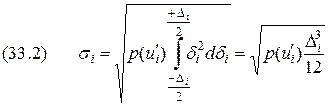 .
.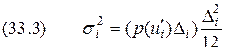 ,
,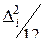 равномерно распределенного на этом шаге сигнала, умноженной на вероятность
равномерно распределенного на этом шаге сигнала, умноженной на вероятность 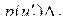 попадания мгновенного значений сигнала в пределы данного шага. Дисперсия полной ошибки квантования
попадания мгновенного значений сигнала в пределы данного шага. Дисперсия полной ошибки квантования 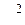 для всей непрерывной шкалы мгновенных значений сигнала определяется как математическое ожидание дисперсий
для всей непрерывной шкалы мгновенных значений сигнала определяется как математическое ожидание дисперсий 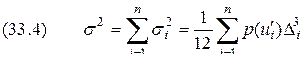 .
.
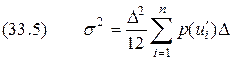 .
.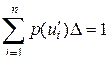 ,
,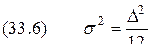 .
.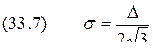 .
.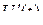 . Ошибку квантования
. Ошибку квантования 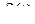 , которая изменяется во времени и также представляет собой случайный процесс, называют шумом квантования:
, которая изменяется во времени и также представляет собой случайный процесс, называют шумом квантования: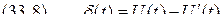 .
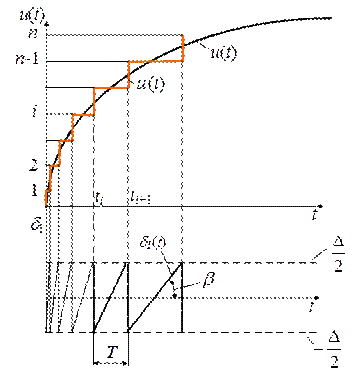
.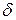 можно определить по реализации
можно определить по реализации 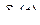 (рис.). В пределах каждого квантования
(рис.). В пределах каждого квантования 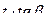 , где
, где 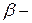 переменный угол наклона прямой. При размещении уровней квантования в середине каждого шага математическое ожидание ошибки равно нулю, а её среднеквадратическое значение определяется выражением
переменный угол наклона прямой. При размещении уровней квантования в середине каждого шага математическое ожидание ошибки равно нулю, а её среднеквадратическое значение определяется выражением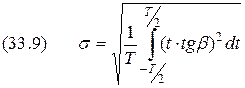 .
.
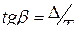 , то
, то 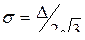 , что соответствует ранее полученному значению (см. выражение (33.7)).
, что соответствует ранее полученному значению (см. выражение (33.7)).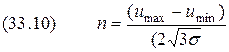 .
.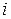
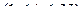
 изменяется в интервале от 0 до 1,
изменяется в интервале от 0 до 1, 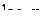 отрицателен и, следовательно,
отрицателен и, следовательно,  положительна.
положительна. ограниченность очевидна. Остаётся определить предел, к которому стремится слагаемое
ограниченность очевидна. Остаётся определить предел, к которому стремится слагаемое 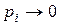 . Так как
. Так как 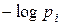 при этом неограниченно возрастает:
при этом неограниченно возрастает: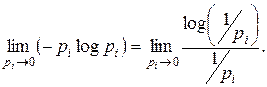
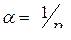 и воспользовавшись правилом Лопиталя, получим
и воспользовавшись правилом Лопиталя, получим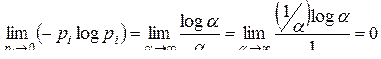 .
.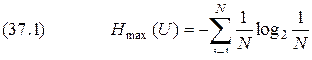 .
.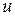 с двумя состояниями
с двумя состояниями  и
и 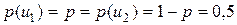 .
.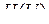 в функции
в функции 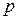
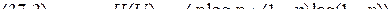
 приведен на рис.... При
приведен на рис.... При 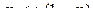 частная неопределенность, которая приходится на состояние
частная неопределенность, которая приходится на состояние  .
. . Под объединением двух источников
. Под объединением двух источников  , который характеризуется вероятностями
, который характеризуется вероятностями 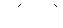 всех возможных состояний
всех возможных состояний 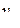 источника
источника 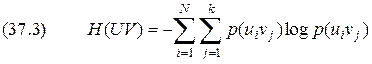 .
.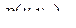 вероятность совместной реализации состояний
вероятность совместной реализации состояний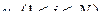 и
и  .
.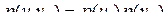 .
.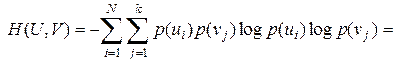
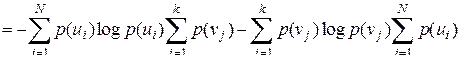 .
.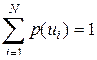 и
и 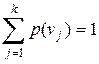 ,
,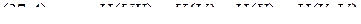 .
.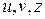 имеем
имеем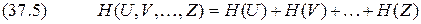 .
.


