
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Laboratory-practical classes onСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
фГБоу во «КАЗАНСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ имени Н.Э. БАУМАНА»
кафедра биологической и неорганической химии
Manual Laboratory-practical classes on Chemistry course
FOR ENGLISH-SPEAKING STUDENTS OF VETERINARY MEDICINE FACULTY
PART 1
Казань 2017 ББК 24я73 УДК 621.357:941 Печатается по решению Ученого совета факультета биотехнологии и стандартизации ФГБОУ ВО «Казанская государственная академия ветеринарной медицины им. Н.Э. Баумана» От июня 2017 года, протокол №
Рецензенты: Доцент кафедры ХТОСА ИХТИ ФГБОУ ВО КНИТУ, к.х.н. З.Л. Ахтямова; Заведующий кафедрой фармакологии и токсикологии ФГБОУ ВО КГАВМ, д.в.н., Ф.А. Медетханов
Микрюкова, Е.Ю. УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ Manual Laboratory-practical classes on chemistry course FOR ENGLISH-SPEAKING STUDENTS OF veterinary MEDICINE FACULTY. PART 1 / Е.Ю. Микрюкова, А.В. Жарехина, А.М. Галиева – Казань: КГАВМ, 2017. – 66 с.
Учебно-методическое пособие по неорганической химии предназначено для иностранных студентов первого курса факультета ветеринарной медицины. По каждой теме приводится необходимый теоретический материал, а также примеры решения типовых задач, задания для подготовки к промежуточному и итоговому контролю, образцы тестов и указания к выполнению лабораторных работ. В конце приведены экзаменационные вопросы и необходимый справочный материал
ã МикрюковаЕ.Ю., Жарехина А.В., Галиева А.М. ã федеральное государственное бюджетное образовательное учреждение высшего образования «Казанская государственная академия ветеринарной медицины Н.Э. Баумана», 2017 Class 1. Topic: Concentration units.
The relative content of a substance is known as it’s concentration, that on other hand means the content of solute (in g or Mol) in unit of mass or volume of solution or solvent. We use approximate and exact ways of concentration expressions. To characterize the concentration approximately we usually use following definitions: dilute, concentrated, unsaturated, saturated, supersaturated. The exact ways of concentration expression are the following: 1.Mass fraction or percentage of solute ω(x) is the ratio of solute mass(m(x)) and the solution mass (m(solution)), this value is dimensionless and is expressed in fractions from unit or in percent (%) and likewise in thousandth fractions (‰) or in millionth fractions (mln-1). For instance ω(x) = 0,005 = 0,5% =5‰ = 5000 mln-1. In medical literature mass fraction is often expressed in gram-percent (g%) (equally percentage), milligram-percent (mg% or 10-3 g%) and mikrogram-percent (mkg % or 10-6 g%). Therefore ω(x)= 0,005 = 0,5 g% = 500 mg% = 500000 mkg%. For example 5% solution is 5-percent solution or solution with mass fraction of solute equal to 5% or 0,05. 2. Mole fraction χ(x) – is the relation of number of moles of solute ν(x) to the total number of moles of all components of solution Σν(xi). This is dimensionless value, expressed in fractions of unit or in percent. 3.Volume fraction: φ(x) –is the relation of volume of the solution component (liquid) V(x) to the total volume of solution (liquids mixter) V(solution). It is likewise expressed in fractions of unit or in percent. 4.Molar concentration or molarity C(x) is the relation of number of moles of solute ν(x) to the volume of solution V(solution), whose dimension is mol/l. For instance, 0,1M solution means decimolar solution or solution with molarity of solute equal to 0,1 mol/l. 5. Molar concentration of equivalent (normality) C(1/z x) is the relation of number of moles of equivalent of solute ν(1/z x) to the volume of solution; its dimension is mol/l. The term “equivalent” is connected with some definite reaction in which this substance takes part. Equivalent (1/z x) is the conventional or real particle of X which in given acid-base reaction is equivalent to one proton or to one electron in given oxidation-reduction reaction. Equivalent of one-basic acids or one-acidic bases is always real particle that is the molecule X. As for polyprotic acids and multi acidic bases their equivalent can be equal to the real molecule X or some it’s fraction- 1/z x. Number, that point to fraction of real particle, which is equivalent to one proton in acid-base reactions or to one electron in ox-red reactions is named factor of equivalence (feq(x) or 1/z x). Examples of determinations of equivalents are given below. If two substances take part in chemical reaction such as X1 and X2,according to the “law of equivalents” number of moles of equivalent of the first consumed substance ν(1/z x1) is equal to number of moles of equivalent of the second: ν(1/z x2) or: ν(1/z x1) = ν(1/z x2). If acid-base reaction proceeds completely we mast take into account that Z is the basicity of the acid or acidity of the base and as for salts is the product of number of metal atoms, forming this salt, and metal’s valency. One mole of equivalents of X contains Avogadro’s number of particles (6,02∙1023 of X equivalents). Molar mass of equivalent 1/z∙x is determined as product of equivalent’s factor and molar mass of the substance: M(1/z∙x) = 1/z∙M(x) Solutions with definite normality C(1/z∙x) are used for absolutely concrete reactions. For instance: 0,01N solution whose normality is equal to 0,01 Mol/l. 6. Molality (molal concentration) of the solution b(X) is determined as relation of number of moles of solute ν(x) to the mass of solvent m(solvent); dimension - Mol/kg. May be assumed the following symbolizes: for normality: N(X) instead of C(1/z∙x); for molality Cm(X) instead of b(X). Titre (or mass concentration) t(X) is the relation of solute mass to the volume of solution; dimension – g/ml. Formulas used to calculate all concentration mentioned above are given in the table 3 placed in appendix. According to the “law of equivalents” if solutions of two substances with volume of V(sol-n X1) and V(sol-n X2) and normalities of C(1/z∙x1) and C(1/z∙x2) and titres of t(X1) and t(X2) correspondingly react, we can write the equations V(s-n X1) C(1/z∙X1) m(X1) V(s-n X1)∙t(X1) M(1/z∙X1) ———— = ————; ——— = —————— = ———— V(s-n X2) C(1/z∙X2) m(X2) V(s-n X2)∙t(X2) M(1/z∙X2) Tasks with their solutions
Normality
8. How many grammes of Na2CO3 are required to prepare 1,5 L of solution with molar concentration of equivalent equal to 0,15 mol/l. This solution is prepared for complete reacting.
V(s-n) = 1,5 L The reaction proceeds according to:
m(Na2CO3) =? Na2CO3+ H2SO4 =Na2SO4 + H2O + CO2 feq = 1/2. M(1/2 Na2CO3)=1/2 M(Na2CO3) =106/2 = 53 g/mol m(Na2CO3)=C(1/2Na2CO3)∙V(s-n)∙M(1/2 Na2CO3)= =0,15∙1,5∙53 = 11,925 g The answer: 11,925 g.
9. How many ml of CaCl2 solution with mass fraction of 10% (ρ= 1,04 g/ml) are required to prepare 2 L of solution with molarity of equivalent 0,05 mol/l. This solution is prepared for the reaction proceeding completely.
ω1%(CaCl2) = 10%= 0,1 CaCl2 + 2AgNO3= 2 AgCl + Ca(NO3)2 ρ(s-n 1)=1,04 g/ml feq = ½; M(1/2 CaCl2)= 1/2·111= 55,5(g/mol) V(s-n 2) = 2L m(CaCl2) = V(s-n 1)·ρ(s-n 1)·ω1(CaCl2)= C2(1/zCaCl2) = 0,05 mol/l =C2(1/2 CaCl2)·M(1/2 CaCl2)·V(s-n2) =>
V(s-n 1) =? V(s-n1) = —————————————— = ρ(s-n 1) ∙ ω1(CaCl2) 0,05∙2∙55,5 = ————— = 53,35(ml) 1,04 ∙ 0,1 The answer: 53,35 ml.
10. Determine the normality of 50,1% H2SO4 solution with density 1,4 g/ml. Solution is applied for reaction, proceeding completely.
ω1% (H2SO4) =50,1% Reaction equation: ρ(s-n 1)=1,4 g/ml H2SO4 + 2KOH = K2SO4 + 2 H2O feq(H2SO4) = ½; M(1/2 H2SO4)= 98/2= 49(g/mol) C(1/Z H2SO4)=? Assume that V(s-n) = 1000 ml =1L
Then m(s-n) = ρ(s-n)· V(s-n) =1,4·1000 = 1400 (g) ν(1/z H2SO4) m (H2SO4) C(1/Z H2SO4)= —————— = ——————— V(s-n) M(1/2H2SO4)∙V(s-n)
m(s-n)∙ ω1(H2SO4) 1400 ∙ 0,501 = —————————— = ————— = 14,2 mol/l M(1/2 H2SO4))· V(s-n) 49·1
The second version: using the formula from table 3 of appendix:
10∙ ρ · ω1(H2SO4) 10∙1,4∙50,1 C(1/Z H2SO4) = ——————— = ————— =14,2 mol/l M (1/2H2SO4) 49
The answer: 14,2 mol/l
11. Determine the normality of 0,5 M Al2(SO4)3 solution destined for reaction of alluminium hydroxide formation.
Data: Solution: C(Al2(SO4)3) =0,5 M Reaction equation:
C(1/Z Al2(SO4)3) =? feq (Al2(SO4)3) = 1/6 C(1/6Al2(SO4)3) = 6•C(Al2(SO4)3)= 6∙0,5=3 Mol/l
The answer:3 mol/l (3N)
12. Determine the titre of 0,15 N Na2CO3 solution destined for full ion-exchange reaction.(look at task №8)
C(1/2 Na2CO3) = 0,15 mol/l feq (Na2CO3) =1/2;
C(1/2 Na2CO3)∙ M(1/2 Na2CO3) t(Na2CO3)=? t(Na2CO3)= ————————————— = 1000 0,15∙53 = ———— = 0,007950 g/ml 1000 The answer: 0,007950 g/ml
Molality
13. Calculate the molality of 40% HNO3- solution.
ω (HNO3) = 40% Assume that m(s-n) = 100g, then m(HNO3) = m(s-n)∙ ω (HNO3) = 100·0,4 =40 g.
υ(HNO3) m(HNO3) 40 b(HNO3) = ———— = ——————— = ——— = 10,6 (H2O) M(HNO3)•m(H2O) 63•0,06 The answer:10,6 Mol/kg
Laboratory work
Concentrated solution
Fulfillment of the work Take the task from your teacher - to prepare from concentrated solution the certain volume of solution with less concentration. Calculate, how many (ml) of initial solution are required to prepare solution with given concentration. Then find the water volume required to obtain this solution. Find the solution density using the table. Show your calculations to teacher. After check prepare given solution by mixing obtained volumes of initial solution and water. To prepare solution with certain concentration use: measured flask, measured cilinder, pipette with help of which carry the determined volume of liquid over into the measured flask to our solution till the mark and mix. Addition of the water is carried on quickly at the beginning and closer to mark, below 1-2 sm from the mark, by drops. Estimation of liquid level in measured flask and measured cilinder is carried on by low meniscus. Mixing of the solution in the flask is carried on by shake and rotation. Prepared solution have to be given out to the labassistent.
Example of calculation: It is required to prepare 50 ml of 0,05 N Na2CO3 solution from 0,2 M Na2CO3 solution if feq(Na2CO3) = ½. Calculation: ν2(1/2 Na2CO3)= C2(1/2 Na2CO3)·V(s-n 2) =0,05·0,05 = 0,0025 (Mol) ν(Na2CO3)=1/2ν2(1/2 Na2CO3)=1/2 ·0,0025 = 0,0012(mol) ν(Na2CO3) 0,00125 V(s-n 1) = ————— = ———— =0,00625L or 6,25 ml of 0,2 M solution. C(Na2CO3) 0,2
Class 2
Questions for self-control 1. What substances are called electrolytes? Tell the differences between aqueous electrolyte solutions and nonelectrolyte solutions. 2. How can you explain the electrolytic dissociation (ionization). 3. What values are the quantitative characteristics of electrolytic dissociation process (ionization). 4. What groups are all electrolytes conventionly divided by in dependence on their dissociation degrees. Give the examples. 5. What is the activity? How does it depend on the analytical concentration. 6. What is the activity coefficient, how is its value changing if the solution is being deluted. 7. What values define the activity factor for each ion and what formula can express this dependence. 8. What does it mean the ionic strength of solution and how is it determined. 9. Write down the relationship between ionic strength and molarity of diluted solutions for a) binary electrolytes of one charged and bi-charged ions (as KCl and ZnSO4; b) three – and fore-ionic electrolytes such as Na2SO4 and FeCl3. 10. How and why does the degree of dissociation of weak electrolyte depend on the introduction into its solution of the same name ion or on the dilution of the solution. 11. Why is the constant of dissociation (ionization) a more convenient characteristic of electrolyte than the degree of dissociation 12. What formula expresses the law of dilution? Define the bounds of this law application. 13. What factors does the constant of dissociation depend on? 14. In what cases Kdis = C(electrolyte) · α2. Prove the answer. 15. If the electrolyte is strong, we have [Kt+] = C(KtAn), and if the electrolyte is weak: [Kt+] = C(KtAn)· α. Why is it so? 16. How can we calculate the concentration of cation of weak electrolyte KtAn, if we know: a) dissociation constant and molarity of electrolyte b) the constant and degree of dissociation of electrolyte?
Tasks for self-solution
1. Calculate the ionic strength of K2SO4 solution whose molarity is equal to 0,02 M/L. The answer: 0,06 M/L. 2. Determine the ionic strength of the solution, containing 1,62g Ca(HCO3)2 in 250 ml of the solution. The answer: 0,28. 3. Calculate the ionic strength of solution, containing 2,08 g of BaCl2 and 5,85 g of NaCl in 500 ml of solution. The answer: 0,26. 4. Calculate the ionic strength and activity of ions in solution, containing 0,01 M of Ca(NO3)2 and 0,01 M of CaCl2 in 1L of solution. 5. Dissociation degree of acetic acid in 1N; 0,1 N; 0,01N solutions is equal to o,42%, 1,34%, and 4,25% respectively. Calculate Ka for these solutions. Prove that the constant of dissociation doesn’t depend on the concentration of the solution. 6. The dissociation constant of HNO2 equals 5,1·10-4. Calculate the degree of dissociation of its 0,01 M solution and concentration of H+ ions. The answer: 22,6%; 2,26·10-3 M/L. 7. The first dissociation constant of H3PO4 equals 7,11·10-3. Calculate the concentration of H+ -ions in 0,5 M solution if other steps of dissociation are neglected. The answer: 5,5·10-2 M/L. 8. What is the concentration of H+-ions in 1N solution of HCN if its Ka =4,9·10-10? How many grams of ions are contained in 1,5L of acid solution? The answer: 2,21·10-5 M/L; 5,75·10-4 g. 9. Determine the dissociation degree and concentration of OH- -ions in 0,1N solution of NH4OH, if Kb = 1,77·10-5. The answer:1,33%, 1,33 ·10-3 M/L. 10. How many times is the concentration of H+- ions in 1N HNO3 (α = 0,82) as high as the concentration of H+-ions in 1N H2SO4 solution (α = 0,51)? The answer: 1,6 times. 11. How much water should we add to 300 ml of 0,2 M solution of CH3COOH to double the dissociation degree of its acid?The answer: 50 ml. 12. 6,82·1018 molecules and ions are contained in 1L of 0,001M HCOOH-solution. Determine dissociation degree of formic acid. The answer: 13,3%.
Example of a test card on the topic: “The properties of electrolyte solution”
1. What is the molarity of HNO2 solution,if its dissociation degree equals 0,2? Ka= 4·10-4. a) 0,01 b) 0,01 c) 0,02 2. Choose the right formula for the calculation of Ka for acid with α<<0,03. a) α2· C b) α2· C c) α· C ——— 1 – α 3. What is the ionic strength of C-molarity solution of NaCl equal to? a) 0,5 C b) 1C c) 2C
4. What factors does the dissociation constant depend on? a) temperature b)concentration c) solubility in water.
Calculate Ka of acetic acid, if dissociation degree of 0,01 M solution equals 2% at 250C. a) 1,35·10-4 b) 1,75·10-5 c) 9·10-6 The answers to the tasks on the topic “The properties of electrolyte solutions”
Number of question 1 2 3 4 5 Code of answer b b b a c Class 3. Tasks with solutions
1. Solve for pH and pOH of 0,01 M HCl solution if α = 80%
Data: Solution:
α = 80% = 0,8 [H+] = C(HCl)∙ α; pH =-lg [H+]; pOH= 14- pH
2) pH= -lg=8∙10-3 =3 – lg8 = 3-0,9 = 2,1 3) pOH = 14 –2,1 = 11,9 Тhe answer: pH =2,1 pOH = 11,9.
2. Solve for pH of 0,001 M CH3COOH solution if Ka = 1,8 ∙ 10-5
C(CH3COOH) = 1∙10-3 mol/l CH3COOH↔ CH3COO- + H+ Ka = 1,8 ∙ 10-5 pH =-lg [H+];
2) pH = -lg 1,35∙ 10-4 = 4- 0,13 =3,87 The answer: pH =3,87.
3. Solve for pH of solution, containing 0,4 g of NaOH in 2 L (α = 100%)
m(NaOH) = 0,4 g NaOH ↔ Na+ + OH- V(s-n) =2L pH= 14- pOH, pOH= -lg [OH-]; α = 100 m(NaOH)
pH=? M(NaOH)∙ V(s-n) 0,4 1) C(NaOH)= —— = 0,005 mol/l 40∙2 [OH] = 0,005 mol/l 2) pOH = - lg 5∙10-3 = 3- lg5 = 3-0,7 = 2,3 3) pH = 14 – 2,3 = 11,7 The answer: pH =11,7.
4. Solve for pH of 0,1 M NH3 solution if Kb = 1,8 ∙ 10-5
C(NH3) = o,1 mol/l NH3 + H2O ↔ NH4+ + OH-
[OH-]= Kb∙C
2) pOH = 3-lg 1,35 = 3- 0,13 =2,87 3) pH =14- 2,87 = 11,13 The answer: pH =11,13
5. Write down the equations of salts hydrolysis Na3PO4 ,Na2HPO4, NaH2PO4 Find the hydrolysis constants for them. Which salt is hydrolyzed in a greater extent? Ka1 = 7,1 ∙ 10-3, Ka2 = 6,2∙ 10-8, Ka3 =5∙ 10-13 Solution: 1)Na3PO4 + H2O ↔ Na2HPO4 + NaOH, PO43- +H2O ↔ HPO42- + OH-
10-14 1∙10-14 Khyd1 = —— = ——— = 2∙10-2 Ka3 5∙ 10-13
2) Na2HPO4 + H2O ↔ Na2HPO4 + NaOH, HPO42- + H2O↔ H2PO4- + OH-
10-14 1∙10-14 Khyd2 = —— = ——— = 1,6∙10-7 Ka2 6,2∙ 10-13 3) NaH2PO4 + H2O ↔ H3PO4 + NaOH, H2PO4- + H2O↔ H3PO4 + OH-
10-14 1∙10-14 Khyd3 = —— = ——— = 1,4∙10-18 Ka1 7,1∙ 10-3
The answer: Na3PO4 is hydrolyzed in greatest extent.
Class 4 Buffer solutions The solutions of weak acids or weak bases with their salts possess the buffer properties: buffer solutions can be diluted without changing of H+ concentration (pH), buffer solution also tends to keep pH constant even when small amounts of strong acid or base are added to them. The expression for the concentration of H+ and pH in buffer solutions of weak acid HAn and its salt with strong base is applied: C(HAn) [H+] = Ka —————; C(An-) C(An-) C(Salt) pH = pKa + lg ——— = pKa + lg ————, C(HAn) C(acid) where pKa = -lgKa.
In the same way we can calculate the concentration of OH- and pH in buffer solutions of weak bases (KtOH) and their salts with strong acid: C(KtOH) [OH-] = Kb —————; C(Kt+)
C(Kt+) C(Salt) pH = 14 – pKb - lg ——— = 14 – pKb -lg ————, C(KtOH) C(base)
If the buffer solution consists of medium salt (Kt2An) and acidic salt (KtHAn) of bi-basic acid H2An, pH is calculated as: C(An2-) pH = pKa2 + lg ———, where pK2 = - lgK2, exponent of Kafor C(HAn-) H2An for the second step.
If the buffer mixture is formed by acidic salts (Kt2HAn and KtH2An) of three-basic acid H3An, the following equation is used:
C(HAn2-) pH = pK2 + lg ————, C(H2An-) Every buffer solution have its own particular capacity. Number of equivalents of acid or base necessary for changing of pH of 1 L of buffer solution by one unit, is called buffer capacity (B): ν(x) B(x) = ————, when V(buf. sol.) = 1L, or the net equation pH1 - pH2 ν(x) B(x) = —————————, where X –acid or base. V(buf. sol.) ∙│ΔpH│
Tasks with their solutions.
1. 15 ml of 0,03 M-solution HCOOH are added to 15 ml of 0,03 M-solution HCOONa. Calculate pH of derived buffer solution. Ka = 1,77∙10-4.
V1 = V2 = 15 ml The first way:
C1 = C2 = 0,03 m/L [H+] = Ka.C(HCOOH) / C(HCOO-) pH =-lg[H+] Ka = 1, 77∙10-4. 1) [HCOO-] in buf.sol.= 15 ∙ 0,003/30 = 0,015M/L
pH -? 3) [H+] = 1,77∙10-4 ∙ 0,015/0,015 = 1,77∙10-4 4) pH = -lg1, 77∙10-4 = 4 - lg 1,77 = 3,75 The second way: It can be simplified as: [HCOO-] 15∙0,03 pH = pKa + lg————— = 3,75 + lg——— =3,75 [HCOOH] 15∙0,03 The answer: 3,75 2. How will pH of buffer mixture formed by 0,1M solution of CH3COOH and by 0,1 M solution of CH3COONa change if we add: a) 0,001M solution of HCl b) 0,001M NaOH solution? Ka = 1,8∙10-4. Solution: In buffer mixter C(acid) 0,1 [H+] = Ka ———— = 1,8 ∙10-5∙—— = 1,8 ∙10-5 С(salt) 0,1 pH = pKa = - lg1,8∙10-5 = 4,75 If the HCl acid is added: 0,001 0,001 0,001 CH3COONa + HCl = CH3COOH + NaCl
[CH3COOH] = 10-1 + 10-3 = 1,01∙10-1 (Mol/L) [CH3COONa] = 10-1 - 10-3 = 0,99∙10-1 (Mol/L) [H+] =1,8∙10-5∙1,02 = 1,84 ∙10-5(Mol/L) If the NaOH is added: CH3COOH + NaOH = CH3COONa + H2O [H+] =1,8∙10-5∙0,98 = 1,76 ∙10-5(Mol/L) pH = - lg1,76∙10-5 = 5- 0,24 = 4,76 The answer: pH is practically constant.
3. Calculate the buffer capacity of blood serum by acid, if 10 ml of 0,1 N HCl solution are consumed for titration of 50 ml of serum to change pH from 7,4 to 7,0.
pH1 = 7,4 ν(x) pH2 = 7 B(x) = —————————, V(HClsol) =10 ml V(buf. sol.) ∙│ΔpH│ C(HCl) = 0,1 M/L 1) ν(HCl) = 10∙10-3∙0,1 = 10-3
3) 10-3 B(HCl) = ————— = 0,05 (M/L) 50∙10-3∙0,4 The answer: 0,05 (M/L)
Questions for self-control 1. What mixtures are called the “buffers”? 2. What is called conjugate acid, conjugate base? Give the examples of protolytic reactions. 3. What types are the buffer solution divided into? Give the examples. 4. Explain, how the buffer solutions work. As the example take the acetic buffer solution. 5. What is the mechanism of the buffer action, take for example ammonia buffer solution. 6. How should we calculate the concentration of H+ -ions in buffer solution of acidic type. 7. How should we calculate the concentration of H+ -ions in buffer solution of basic type. 8. How should you explain the fact: the addition of small amounts of strong acid and bases, and the dilution does not change the acidity of buffer solutions practically. 9. How should you calculate the pH –values in buffer solutions of acidic or basic type. 10. How do you understand: a) buffer capacity of solution b) buffer strength of solution. 11. 1 ml of 0,5M NH3 solution was added to 20 ml of 1% NH4NO3 (ρ = 1 g/ml). Prepared solution was deluted in measured flask till 100 ml. Calculate the pH of obtained solution. Kb=1,8·10-5, pKb=4,75. The answer: 8,56. 12. 15 ml of 0,2 M K2HPO4 solution are added to 25 ml 0,2M KH2PO4 solution. Calculate the pH of obtained solution. Ka1= 7,6·10-3, pKa1= 2,12; Ka2= 6,3·10-8, pKa2 = 7,2; Ka3=1,3·10-12, pKa3=11,87. The answer: 6,98. 13. 15 ml of 0,15M HCOOK solution are added to 12 ml 0,03 M HCOOH solution. Calculate the pH of obtained solution. Ka= 1,8·10-4, pKa= 3,75. The answer: 4,35. 14. Calculate the pH of solution, 500 ml of which contain 1 g of HCOOH and 1 g of HCOOK. Ka= 1,8·10-4, pKa= 3,75. The answer: 3,49. 15. 0,5% solutions of ammonia and ammonium nitrate are mixed in equal amounts. Calculate the pH of the obtained solution whose density is 1 g/ml; Kb= 1,8·10-5, pKb= 4,75. The answer: 9,92. 16. How many ml of 0,2 M Na2CO3 solution can we add to 10 ml of 0,3 M NaHCO3 solution to prepare the solution with pH = 10? Ka1= 4,4·10-7, pKa1= 6,36; Ka2=4,7·10-11, pKa2 =10,33. The answer: 7 ml. 17. How many grams of 0,2 M Na2CO3 should we add to 100 ml of 0,3 M NaHCO3 solution to prepare the solution with pH 10? Ka1= 4,4·10-7, pKa1= 6,36; Ka2= 4,7·10-11, pKa2 =10,33. The answer: 1,49 g.
Heterogeneous equilibrium
In saturated solution of slightly soluble electrolyte KtAn chemical equilibrium is established: KtAn(solid) ↔ Kt+(s-n) + An-(s-n) The equilibrium is quantitatively characterized by the constant of heterogeneous equilibrium, which is called the solubility product (SP). SP(KtAn)=[KT+]∙[An-] = IP(KtAn) ionic product. In saturated solution SP = IP in unsaturated solution SP>IP, in supersaturated solution SP<IP. Concentration of electrolyte X in saturated solution is called solubility (S(x) in mol/l): S(x) = L(x)/M(X), where L(X) – solubility of electrolyte in gram/ l. The relationship between the solubility and the solubility product of electrolyte in dependence on number of ions in a molecule of electrolyte can be presented in the following table:
Tasks with solutions 1. 2,88∙10-6 g of AgI can be dissolved in 1 liter of water. Calculate the SP (AgI).
Data: Solution: V(H2O) = 1 L AgI(s) = Ag+(aq) + I-(aq) m(AgI) = 2,88∙10-6 g SP(AgI) = [Ag+]∙[I-]
SP(AgI) -? [Ag+] = [I-] = C(AgI) = —————— M(AgI)∙V(sol.)
1)V(solution) = V(H2O) = 1 L; M(AgI) = 23 g/M 2) C(AgI) = 1,225∙10-8 Mol/L 3)SP(AgI) = (1,225∙10-8)2 =1,5∙10-16 The answer: 1,5∙10-16
2. Does the precipitate of Fe(OH)3 appear in the solution containing 1,5∙10-16 Mol/L of FeCl3 and 5∙10-5 Mol/L of NaOH? SP = 3,8∙10-38
C(FeCl3) = 1,5∙10-3M/L Fe(OH)3 (s) = Fe3+(aq) + 3OH-(aq) C(NaOH) = 5∙10-5 M/L SP(Fe(OH)3) = [Fe3+]∙[OH-]3 SP(Fe(OH)3) =3,8∙10-38 1) [Fe3+] = C(FeCl3) = 1,5∙10-3M/L
IP><SP -? 3)Fe(OH)3=[Fe3+]∙[OH-]3=1,5∙10-∙(5∙10-5)=1,9∙10-6 4)IP>>SP, consequently, precipitate is formed. The answer: it is formed.
pH =6 Al(OH)3(s) = Al3+(aq) + 3OH-(aq) SP(Al(OH)3 = 5,1∙10-33. 10-14
[Al3+] -? [H+] 1) [H+]= 10-pH= 10-6 (Mol/L) 2) [OH-]=10-14/10-6 = 10-8 (Mol/L) 5,1∙10-33 3) [ Al3+] = ———— =5,1∙10-9 (Mol/L) (10-8)3 The answer: 5,1∙10-9 (Mol/L) Questions for self-control 1. What equilibrium is called heterogeneous? 2. Derive the expression of solubility product (SP) for slightly soluble salt AgCl. 3. Under what conditions does precipitate appear, dissolve, and exist in equilibrium with the solution. Compare IP (ion product) and SP (solubility product). 4. How does the solubility of a substance change in the presence in it’s saturated solution of the common ion? Prove the answer. 5. Derive the formulas for calculating SP if the solubility (S) is known for the cases: a) BaSO4; b) Mn(OH)2 c) Cr(OH)3 d) Mg3(PO4) f) KtnAnm 6. How many grams (g) of CaSO4 are dissolved in 1 litre of water if SP(CaSO4) = 6,1∙10-5? The answer: 1,062g. 7. 0,001215 g of Ca3(PO4)2 are dissolved in 1 litre of water. Calculate SP (Ca3(PO4)2). The answer: 1∙10-25. 8. Compare the solubility of two salts: AgCl and Ag2CrO4. How many times is one salt as soluble as the another? SP(AgCl) = 1,1∙10-10, SP(Ag2CrO4) = 1,6∙10-12. The answer: silver chromate is 7,3 times as soluble as silver chloride in moles, and 16 times in grams. 9. How many grams (g) of BaSO4 are contained in 100 L of saturated solution, if SP(BaSO4) = 1∙10-10. The answer; 0,23 g. 10. How many grams (g) of AgBr are contained in 10 L of saturated solution, if SP(AgBr) = 4∙10-13. The answer: 1,19∙10-3 g. 11. How many grams (g) of NaOH should we add to 20 ml of the solution, containing 5∙10-5 M MgCl2 to precipitate Mg(OH)2? SP(Mg(OH)2) =1,2∙10-11.The answer: 3,9∙10-4 g. 12. How many milliliters of 2M HCl solution should we add to 20 ml of the 3∙10-2 M Pb(NO3)2 solution, to precipitate PbCl2? SP(PbCl2) = 2,4∙10-4. The answer: 0,94 ml. 13. Is CaSO4 precipitated if we add to 0,1 M CaCl2 solution the equal volume of 0,1 M H2SO4 solution. SP(CaSO4) = 6,1∙10-5. The answer: IP = 4,26∙10-4: CaSO4 is precipitated. 14. What is the value of pH when Mg(OH)2 is precipitated from 2∙10-2 M MgSO4 solution? SP(Mg(OH2) = 1,2∙10-11. The answer: 9,38.
Class 7 Questions for self-control. 1. What is called “the system” in chemical thermodynamics? 2. What do you know about the classification of the “ systems”? 3 When conditions of a system state are called standard conditions? What is “the system state function”? List the state functions. 4. What energy is called “ the internal system energy (U)"? 5. What is the expression of the first law of thermodynamics? Write down the mathematical expression of the law. 6. Under what conditions the change of the internal energy of a system equals the heat has been got by the system from the surroundings. 7. What kind of process is called “ isobaric process”. What is the heat, absorbed by the system when the pressure is constant, spent on? 8. What change of the internal energy does each system tend towards? How can it be expressed? 9. What equation defines the enthalpy and its change? 10. Under what conditions does the change of enthalpy (∆H) equal the heat absorbed from the surroundings? 11. What law is the basic law of thermochemistry? Who is the author? Formulate the law. 12. What is called “the heat effect” of chemical reaction? What equations are called thermochemical? 13. What is called “the heat of formation” and “the heat of combustion”? What units are they expressed in? 14. List the consequences of the Hess’s law. For which determinations are they applied in the thermochemical calculation? 15. In the isolated systems all the spontaneous processes proceed towards the increasing of the chaos. How does the entropy change in such cases? 16. What kind of tendency is expressed by: a) enthalpy factor b) entropy factor? 17. What system state function gives the quantitative characteristic of the simultaneous influence of the enthalpy and the entropy factors. What equation can it be expressed by? 18. What kind of energy is called the “Gibbs energy” (free energy, isobaric – isotermal potential)? 19. How can the change of Gibbs energy (∆G) point at the thermodynamic possibility or impossibility of the spontaneous process proceeding? What value of ∆G determines the equilibrium state of the system? 20. In what correlation are ∆H and T∙∆S a) for the system in the equilibrium? b) if the chemical process proceed to
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 104; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.118 (0.015 с.) |

 Data: Solution:
Data: Solution: C(1/ZNa2CO3)=0,15 mol/l
C(1/ZNa2CO3)=0,15 mol/l Data: Solution:
Data: Solution: C2(1/2CaCl2)•V(s-n2)•M(1/2 CaCl2)
C2(1/2CaCl2)•V(s-n2)•M(1/2 CaCl2) Data: Solution:
Data: Solution:

 Al2(SO4)3 + 6KOH = 2 Al(OH)3 + 3K2SO4
Al2(SO4)3 + 6KOH = 2 Al(OH)3 + 3K2SO4 Data: Solution:
Data: Solution:
 Data: Solution:
Data: Solution: b(HNO3) =? m(H2O) = 100 –40 = 60 g =0,06(kg)
b(HNO3) =? m(H2O) = 100 –40 = 60 g =0,06(kg) C(HCl)=0,01 mol/l HCl↔ H+ + Cl-
C(HCl)=0,01 mol/l HCl↔ H+ + Cl- pH =? pOH =? 1) [H+] =0,01∙0,8 =8∙10-3 (mol/l)
pH =? pOH =? 1) [H+] =0,01∙0,8 =8∙10-3 (mol/l)  Data: Solution
Data: Solution



 pH=? [H+] = Ka∙C
pH=? [H+] = Ka∙C 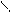

 1) [H+] = 1,8 ∙ 10-5∙ 10-3 = 1,35 ∙ 10-4
1) [H+] = 1,8 ∙ 10-5∙ 10-3 = 1,35 ∙ 10-4 Data: Solution:
Data: Solution: [OH-] = C(NaOH) = ———————
[OH-] = C(NaOH) = ——————— Data: Solution
Data: Solution Kb= 1,8 ∙ 10-5 pH= 14- pOH, pOH= -lg [OH-];
Kb= 1,8 ∙ 10-5 pH= 14- pOH, pOH= -lg [OH-];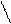

 pH=?
pH=? 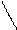


 Data: Solution:
Data: Solution: 2) [HCOOH] in buf.sol.= 15 ∙ 0,003/30 = 0,015M/L
2) [HCOOH] in buf.sol.= 15 ∙ 0,003/30 = 0,015M/L  Data: Solution:
Data: Solution: B-? 2) ΔpH = pH1 – pH2 = 7,4 –7,0 =0,4
B-? 2) ΔpH = pH1 – pH2 = 7,4 –7,0 =0,4 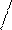

 KtAn
(AgCl)
KtAn
(AgCl)



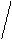 KtAn2
(PbI2)
KtAn2
(PbI2)



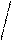 KtAn3
(Fe(OH)3)
KtAn3
(Fe(OH)3)

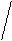 Kt3An2
(Ca3(PO4)2)
Kt3An2
(Ca3(PO4)2)
 5 SP
108
5 SP
108


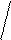 KtnAnm
KtnAnm
 nn∙mm
nn∙mm

 m(AgI)
m(AgI) Data: Solution:
Data: Solution: 2) [OH-] = C(NaOH) = 5∙10-5 M/L
2) [OH-] = C(NaOH) = 5∙10-5 M/L Data: Solution:
Data: Solution: [OH-] = ———; SP(Al(OH)3 )= [ Al3+]∙[OH-]3
[OH-] = ———; SP(Al(OH)3 )= [ Al3+]∙[OH-]3


