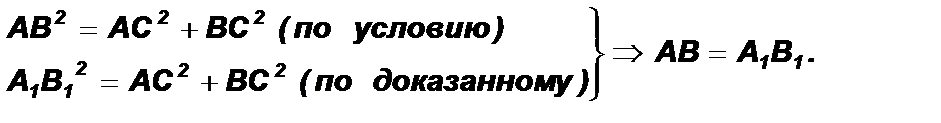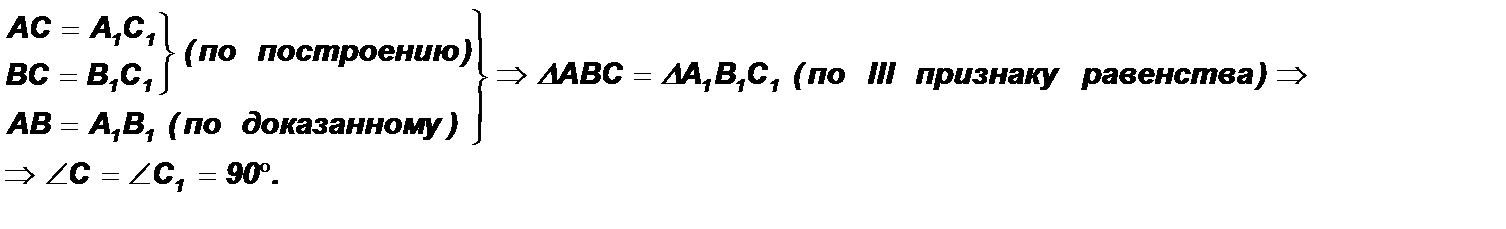Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билеты устного экзамена по геометрии.Стр 1 из 15Следующая ⇒
Билеты устного экзамена по геометрии. Класс. 20 13 -201 4 уч. г. Билет №1 1. Определение и свойства равнобедренного треугольника. Доказательство теоремы о свойстве медианы равнобедренного треугольника, проведенной к основанию. 2. Определение вектора, его длины. Равные и противоположные векторы. Сложение и вычитание векторов. Умножение вектора на число. 3. Задача по теме «Подобие треугольников». Билет № 2 1. Определение равных треугольников. Признаки равенства треугольников (доказательство всех признаков). 2. Деление отрезка на п равных частей. Доказательство теоремы Фалеса. 3. Задача по теме «Метод координат» Билет № 3 1. Пропорциональные отрезки в круге (доказать теоремы о пересекающихся хордах, пересекающихся секущих, секущей и касательной, проведенных из одной точки к окружности). 2. Вывод формулы для вычисления суммы внутренних углов выпуклого многоугольника. 3. Задача «Решение прямоугольного треугольника». Билет № 4 1. Параллельные прямые (определение). Признаки параллельности двух прямых и доказательство этих признаков. 2. Нахождение гипотенузы, катета и острого угла прямоугольного треугольника по данным второму катету и острому углу. 3. Задача «Углы в окружности». Билет № 5 1. Определение вписанного угла. Доказательство теоремы об измерении вписанного угла. 2. Вывод формул площади треугольника 3. Задача по теме «Трапеция». Билет № 6 1. Определение внешнего угла треугольника. Доказать теорему о внешнем угле треугольника. Сумма внешних углов п - угольника. 2. Нахождение значений синуса, косинуса, тангенса и котангенса углов в 300, 450, 600. 3. Задача по теме «Пропорциональные отрезки в круге». Билет № 7 1. Геометрическое место точек. Теорема о геометрическом месте точек, равноудаленных от двух данных точек, в геометрической и аналитической формах.
3. Задача по теме «Элементы треугольника» Билет № 8 1. Определение треугольника. Доказать теорему о сумме углов треугольника. Замечательные точки треугольника: центр тяжести, ортоцентр, центры вписанной, описанной и вневписанной окружностей. 2. Определение тригонометрических функций острого угла прямоугольного треугольника, основные тригонометрические тождества с выводом.
3. Задача по теме «Параллелограмм». Билет № 9 1. Определение прямоугольного треугольника. Признаки равенства прямоугольного треугольника (доказательство всех признаков). 2. Окружность (определение). Формула для вычисления длины дуги окружности (без вывода). Вывод формулы длины дуги окружности. 3. Задача по теме «Задача на построение». Билет № 10 1. Определение параллелограмма. Свойства параллелограмма с доказательством (не менее четырех свойств). 2. Построение биссектрисы угла. Доказать свойство биссектрисы треугольника. Теорема об отношении отрезков биссектрисы треугольника, но которые она делится точкой пересечения биссектрис. 3. Задача по теме «Прямоугольник, квадрат». Билет № 11 1. Доказать признаки параллелограмма. Построение параллелограмма по двум сторонам и диагонали. 2. Определение вневписанной окружности. Теорема о центре вневписанной окружности. 3. Задача по теме «Векторы». Билет № 12 1. Определение прямоугольника. Доказать свойства и признаки прямоугольника. 2. Выражение расстояния между двумя точками через координаты этих точек (три случая). 3. Задача на тему «Окружность». Билет № 13 1. Определение ромба. Доказать свойства и признаки ромба. Вывод формулы
2. Выражение радиуса окружности, вписанной в прямоугольный треугольник через его стороны (вывод формулы). 3. Задача по теме «Биссектриса внутреннего угла треугольника». Билет № 14 1. Построение отрезков х= 2. Определение вписанного четырехугольника. Доказательство свойства углов вписанного четырехугольника. 3. Задача по теме «Теорема синусов». Билет № 15 1. Определение средней линии треугольника и трапеции. Доказательство теорем о средней линии треугольника и трапеции. 2. Построение окружности, вписанной в треугольник и описанной около него. 3. Задача по теме «Векторы». Билет № 16 1. Определение подобных треугольников. Сформулировать лемму о подобии треугольников. Сформулировать и доказать признаки подобия треугольников. 2. Построение касательной к окружности (два случая).
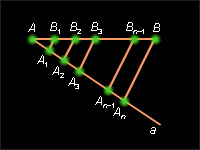
3. Задача по теме «Четырехугольники». Билет № 17 1. Вывод формулы Герона. 2. Свойство чевианы о разбиении площади треугольника на части. Теоремы о «ласточкином хвосте». 3. Задача на тему «Задачи на построение». Билет № 18 1. Вывод формул площадей параллелограмма 2. Доказать теорему об отношении отрезков медиан, на которые они делятся центром тяжести. 3. Задача по теме «Векторы». Билет № 19 1. Трапеция (определение). Вывод формулы площади трапеции. Теорема о четырех точках трапеции (доказательство). 2. Уравнение окружности (вывод). Взаимное расположение прямой и окружности. 3. Задача по теме «Решение треугольника». Билет № 20 1. Теорема Пифагора (прямая и обратная). Пифагоровы тройки чисел, египетский треугольник. 2. Доказательство теоремы о градусной мере угла между хордой и касательной, проведенной через ее конец. Построение касательной к окружности, проходящей через данную точку, не лежащую на окружности. 3. Задача по теме «Подобие». Билет № 21 1. Теорема синусов. Следствие из теоремы. 2. Доказательство теорем об углах, образованных пересекающимися хордами и секущими, проведенными из одной точки к окружности. 3. Задача по теме «Метод координат». Билет № 22 1. Теорема косинусов. Следствие из теоремы. 2. Построение прямой, параллельной данной. Построение касательной, проходящей через данную точку, не лежащую на данной окружности. 3. Задача по теме «Подобие». Билет № 23 1. Теорема об отношении площадей треугольников, имеющих по одному равному углу. Вывод формул площадей треугольника через радиусы вписанной и описанной окружностей. 2. Описанный четырехугольник. Свойство сторон описанного четырехугольника. Формула площади выпуклого четырехугольника 3. Задача по теме «Окружность». Билет № 24 1. Определение подобных многоугольников. Построение многоугольника, подобного данному. Теоремы об отношении периметров и площадей подобных многоугольников. 2. Неравенство треугольника. 3. Задача по теме «Элементы треугольника». Билет № 25
2. Доказать тождества:
3. Задача по теме «Подобие». Билет №1 Билет № 2 1. Определение равных треугольников. Признаки равенства треугольников (доказательство всех признаков).
АВ = А1В1; АС = А1С1; ВС = В1С1; Ð А = Ð А1; Ð В = Ð В1; Ð С = Ð С1. Обозначение равенства треугольников: ∆ АВС = ∆ А1В1С1. Доказательство Равенство отрезков AB 1 = B 1 B 2 =... = B n – 1 B следует непосредственно из теоремы Фалеса.
3. Задача по теме «Метод координат».
Билет № 3 1.
Теорема о пропорциональных отрезках хорд. Произведения отрезков хорд, пересекающихся внутри круга, равны.
Доказательство: 1). Докажем подобие треугольников ADM и BCM:

2). Из подобия треугольников: Теорема 2. Квадрат отрезка касательной, проведенной из точки, лежащей вне круга, равен произведению отрезка секущей на ее внешнюю часть. Доказательство: 1). Пусть секущая А D проходит через центр окружности О. Тогда OB – радиус окружности, AB – касательная к окружности. По свойству касательной OB ^ AB. 2). Из D A О B (Ð ABO = 90°) по теореме Пифагора:
Билет № 4 Задача «Углы в окружности». Билет № 5 Доказательство: 1) Пусть D АВС – остроугольный, тогда BN ^ AC лежит внутри треугольника. 2) Пусть D АВС – тупоугольный с тупым углом С и BN ^ AC лежит внутри треугольника.
Доказательство:
Задача по теме «Трапеция». Билет № 6 1. Определение внешнего угла треугольника. Доказать теорему о внешнем угле треугольника. Сумма внешних углов п - угольника. Построение внешнего угла: Чтобы построить внешний угол треугольника, нужно продлить соответственную сторону треугольника. При каждой вершине треугольника можно построить два внешних угла. Они равны между собой, так как являются смежными с одним и тем же углом.
Дано: ∆АВС. Доказать: Доказательство:
2. Нахождение значений синуса, косинуса, тангенса и котангенса углов в 300, 450, 600. Рассмотрим прямоугольный равнобедренный треугольник с углом при основании, равным 45°. Пусть катеты его равны a. Тогда по теореме Пифагора его гипотенуза будет равна Рассмотрим равносторонний треугольник ABC со стороной, равной a. Проведем в нем медиану BD. Получим треугольник ABD – прямоугольный с острым углом при вершине B и стороной Билет № 7 Пусть геометрическая фигура имеет характерное свойство, определяющее, какие точки принадлежат фигуре. Тогда про эту фигуру говорят, что она является множеством точек, обладающих данным свойством (или геометрическим местом точек, обладающих данным свойством). Примеры: Пусть дан угол со сторонами m и n и вершиной А, где b – биссектриса угла. Возьмем произвольную точку D на биссектрисе b и опустим из нее перпендикуляры на стороны m и n. Рассмотрим полученные треугольники ABD и ACD.
Ð ABD = Ð ACD = 90°; Ð BAD = Ð CAD (b – биссектриса); AD – общая; D ABD = D ACD (как прямоугольные по гипотенузе и острому углу). Þ BD = CD. Характерное свойство биссектрисы угла (обратная теорема). Точка угла, равноудаленная от его сторон, лежит на биссектрисе угла.
Пусть дан угол со сторонами m и n и вершиной А. Возьмем произвольную точку D внутри угла таким образом, что перпендикуляры, опущенные из нее на стороны m и n угла А равны. Рассмотрим полученные треугольники ABD и ACD. Ð ABD = Ð ACD = 90°; BD = CD; AD – общая; D ABD = D ACD (как прямоугольные по гипотенузе и катету). Þ Ð BAD = Ð CAD Þ b – биссектриса Ð А. Определение 1. Пусть фигура имеет характерное свойство, определяющее, какие точки принадлежат фигуре. Тогда про эту фигуру говорят, что она является множеством точек, обладающих данным свойством или геометрическим местом точек, обладающих данным свойством. Определение 2. Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла. Определение 1. Прямая, перпендикулярная к отрезку и проходящая через его середину, называется серединным перпендикуляром к данному отрезку. Характерное свойство серединного перпендикуляра (прямая теорема). Каждая точка серединного перпендикуляра равноудалена от его концов.
Пусть дан отрезок АВ и серединный перпендикуляр к нему n, пересекающий отрезок АВ в точке С. Возьмем произвольную точку D на серединном перпендикуляре n и соединим ее с концами отрезка АВ отрезками AD и BD. Рассмотрим полученные треугольники A С D и В CD. Ð A С D = Ð В CD = 90°; АС = C В (n – серединный перпендикуляр); D С – общая; D A С D = D В CD (как прямоугольные по двум катетам). Þ А D = В D. Характерное свойство серединного перпендикуляра (обратная теорема). Точка, равноудаленная от концов отрезка, лежит на его серединном перпендикуляре. Доказательство:
Построим DC ^ AB. Рассмотрим полученные треугольники A С D и В CD. Ð A С D = Ð В CD = 90°; А D = В D (по условию); D С – общая; D A С D = D В CD (как прямоугольные по гипотенузе и катету). Þ АС = СВ. Определение 2. Пусть фигура имеет характерное свойство, определяющее, какие точки принадлежат фигуре. Тогда про эту фигуру говорят, что она является множеством точек, обладающих данным свойством или геометрическим местом точек, обладающих данным свойством. Определение 3. Серединный перпендикуляр к отрезку – это геометрическое место точек, равноудаленных от концов отрезка. Доказательство: Площадь квадрата
Билет № 8 1. Определение треугольника. Доказать теорему о сумме углов треугольника. Замечательные точки треугольника: центр тяжести, ортоцентр, центры вписанной, описанной и вневписанной окружностей.
Треуго́льник — многоугольник, имеющий 3 вершины и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки. Теорема о сумме углов треугольника: Сумма внутренних углов треугольника равна 180°.
Доказать: Доказательство: 1. Проведем
Следствие 1. У любого треугольника хотя бы два угла острые. Допустим, что у треугольника один острый угол или вообще нет острых углов. Тогда у этого треугольника есть хотя бы два угла, каждый из которых не меньше 90°, а сумма этих углов не меньше 180°. Это невозможно, так как сумма углов треугольника равна 180°. Следствие 2. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то и третьи углы этих треугольников равны. Допустим, что у треугольников АВС и МРТ соответственно равны углы: ÐА = ÐМ, ÐВ = ÐР. Тогда ÐС = 180° - (ÐА + ÐВ), ÐТ = 180° - (ÐМ + ÐР). Следовательно, ÐС = ÐТ. Следствие 3. У прямоугольного треугольника сумма острых углов равна 90 °. Так как у прямоугольного треугольника один из углов прямой, то сумма двух других его углов равна 180° - 90° = 90°. Следствие 4. У равнобедренного прямоугольного треугольника острые углы имеют градусную меру 45 °. Так как у прямоугольного треугольника один из углов прямой, то сумма двух других его углов равна 180° - 90° = 90°. Поскольку эти углы равны, то градусная мера каждого 90°: 2 = 45°. Следствие 5. У равностороннего треугольника все углы имеют градусную меру 60 °. Так как у равностороннего треугольника все углы равны между собой, а их сумма равна 180°, то градусная мера каждого угла равна 180°: 3 = 60°.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. CM – медиана, проведенная к стороне АВ (АМ = МВ). Высотой треугольника называется отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону. ВР – высота, опущенная на сторону АС.
Точка пересечения высот треугольника называется ортоцентром треугольника. В отличие от других замечательных точек треугольника ортоцентр треугольника может находиться не только внутри треугольника, но и вне его.
Билет № 9 1. Определение прямоугольного треугольника. Признаки равенства прямоугольного треугольника (доказательство всех признаков). Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой. 1. Если два катета одного треугольника соответственно равны двум катетам другого треугольника, то такие прямоугольные треугольники равны (частный случай первого признака равенства треугольников).
2. Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).
Билет № 10 1. Определение параллелограмма. Свойства параллелограмма с доказательством (не менее четырех свойств). Определение 1. Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом. У каждого параллелограмма четыре вершины, четыре стороны, четыре угла. Две стороны, имеющие общие концы, называются смежными. У каждого параллелограмма две диагонали – отрезки, соединяющие противоположные вершины параллелограмма. Сумма углов параллелограмма равна 360°. Свойства параллелограмма.
Свойство 1. У параллелограмма противоположные стороны равны и противоположные углы попарно равны. Доказательство: Проведем диагональ АС. АС – общая; Ð ВАС = Ð АС D (внутренние накрест лежащие при АВ II BC и секущей АС); Ð ВСА = Ð СА D (внутренние накрест лежащие при А D II BC и секущей АС); Þ D АВС = D А D С (по 2 признаку).АВ = CD; BC = AD; Ð В = Ð D. Ð А = Ð ВАС + Ð С AD; Ð С = Ð АС B + Ð АС D; Þ Ð А = Ð С. Свойство 2. У параллелограмма углы, прилежащие к одной стороне, в сумме дают 180°. Доказательство: Ð В + Ð А =180° (внутренние односторонние при ВС II AD и секущей А B). Ð B + Ð С =180° (внутренние односторонние при A В II CD и секущей BC). Ð D + Ð C =180° (внутренние односторонние при ВС II AD и секущей CD). Ð A + Ð D =180° (внутренние односторонние при A В II CD и секущей AD). Свойство 3. Диагонали параллелограмма точкой пересечения делятся пополам.
АВ = С D (по первому св-ву параллелограмма); Ð A В O = Ð ODC (внутренние накрест лежащие при АВ II CD и секущей BD); Ð ВА O = Ð O С D (внутренние накрест лежащие при А B II CD и секущей АС); Þ D АВ O = D OD С (по 2 признаку).В O = OD; AO = OC.
2. Построение биссектрисы угла. Доказать свойство биссектрисы треугольника. Теорема об отношении отрезков биссектрисы треугольника, но которые она делится точкой пересечения биссектрис. Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла. Построение биссектрисы данного угла: AD – биссектриса. Теорема о биссектрисе угла треугольника. Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные соответствующим боковым сторонам.
Доказательство: Пусть АС = b, AB = c, BC = a. Если AD = x, то DC = b – x. Составим пропорцию:
Билет № 11 АВС D – параллелограмм.
Дано: ABCD – четырехугольник; АС АВС D – параллелограмм. 2. Определение вневписанной окружности. Теорема о центре вневписанной окружности. 3. Задача по теме «Векторы». Билет № 12 1. Определение прямоугольника. Доказать свойства и признаки прямоугольника. Определение 1. Прямоугольником называется параллелограмм, у которого все углы прямые. Билет № 13 1. Определение ромба. Доказать свойства и признаки ромба. Вывод формулы
Определение 1. Ромбом называется параллелограмм, все стороны которого равны. Доказательство: Рассмотрим D АВС. АВ = ВС, АО = ОС. Þ ВО – высота и биссектриса Ð АВ C. Þ ВС ^ AD; Ð АВ O = Ð C В O. Рассмотрим D АВ D. АВ = AD, B О = О D. Þ A О – высота и биссектриса Ð B А D. Þ Ð В AO = Ð OAD. Признаки ромба. Признак 1. Если диагонали параллелограмма взаимно перпендикулярны, то параллелограмм является ромбом.
Доказать: АВС D – ромб. Доказательство: АО = ОС (по свойству диагоналей параллелограмма); ВО = О D (по свойству диагоналей параллелограмма); Ð АОВ = Ð ВОС = Ð СО D = Ð АО D = 90°; Þ D АОВ = D ВОС = D СО D = D AOD (как прямоугольные по двум катетам); Þ АВ = ВС = С D = AD; Þ АВС D – ромб.
Доказать: АВС D – ромб. Доказательство: АО – общая; ВО = О D (по свойству диагоналей параллелограмма); Ð ВАО = Ð DA О (по условию); Þ D АОВ = D AOD (как прямоугольные по катету и прилежащему острому углу); Þ АВ = AD Þ АВС D – ромб. 2. Выражение радиуса окружности, вписанной в прямоугольный треугольник через его стороны (вывод формулы). 3. Задача по теме «Биссектриса внутреннего угла треугольника». Билет № 14 1. Построение отрезков х= Проводим прямую АС. Так как центр описанной около четырехугольника окружности равноудален от его вершин, то он принадлежит серединным перпендикулярaм к его сторонам и диагоналям. Обратно, если серединные перпендикуляры к трем сторонам четырехугольника пересекаются в одной точке, то эта точка будет равноудалена от всех его вершин и поэтому будет центром описанной около него окружности. Итак, для того, чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы серединные перпендикуляры к трем его сторонам пересекались в одной точке.
Теорема. Для того, чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы сумма его противоположных углов была равна 180 ° (т. е. суммы его противоположных углов были равны). Необходимость этого условия очевидна: сумма углов A и C вписанного четырехугольника ABCD измеряется полусуммой дуг BCD и BAD, составляющих полную окружность, и потому равна 180 °. Доказательство: По теореме о градусной мере вписанного угла в окружности Теорема (обратная). Если сумма противоположных углов четырехугольника равна 180 °, то около него можно описать окружность.
Предположения: Билет № 15 1. Определение средней линии треугольника и трапеции. Доказательство теорем о средней линии треугольника и трапеции. Определение 1. Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Свойство средней линии треугольника. Средняя линия треугольника параллельна основанию треугольника и равна его половине.
Доказать: MN II AC; Доказательство: 1. Продолжим MN за точку N и на продолжении отложим PN = MN. Рассмотрим D MBN и D NPC. BN = NC (по определению средней линии); MN = NP (по построению); Ð MN В = Ð PNC (вертикальные); Þ D M В N = D NPC (по 1 признаку) Þ Ð BMN = Ð NPC (внутренние накрест лежащие) Þ АВ II PC. 3. CP = MB (из равенства треугольников); AM = MB (по определению средней линии); Þ CP = А M. 5. А M II PC; AM = PC Þ AMPC – параллелограмм Þ AC = MP; AC II MP. 6. MP = 2 MN (по построению) Þ MN = 0,5 AC. 7. AC II MP; MN Ì MP; Þ MN II AC. Определение 2. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Свойство средней линии трапеции. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
Доказательство: Рассмотрим D N ВС и D NDE. С N = ND (по условию); Ð В N С = Ð END (вертикальные); Ð B С N = Ð NDE (внутренние накрест лежащие при BC II AD и секущей CD); D N ВС и D NDE (по 2 признаку) Þ BN = NE; BC = DE. Рассмотрим D A В E. MN – средняя линия MN II AD; MN =0,5 AE. AE = AD + DE = AD + BC Þ 2. Построение окружности, вписанной в треугольник и описанной около него. Чтобы построить вписанную окружность, достаточно: Задача по теме «Векторы». Билет № 16 Билет № 17 1. Вывод формулы Герона. Билет № 18 1. Вывод формул площадей параллелограмма 2. Доказать теорему об отношении отрезков медиан, на которые они делятся центром тяжести. 3. Задача по теме «Векторы». Билет № 19 1. Трапеция (определение). Вывод формулы площади трапеции. Теорема о четырех точках трапеции (доказательство). Определение 1. Трапецией называется четырехугольник, две стороны которого параллельны, а две другие – непараллельные. Билет № 20 4. Теорема Пифагора (прямая и обратная). Пифагоровы тройки чисел, египетский треугольник.

Доказательство: Доказательство: 1). Пусть в треугольнике АВС АВ2 = АС2 + ВС2. Докажем, что угол С – прямой. 2). Рассмотрим прямоугольный треугольник А1В1С1 с прямым углом С1, у которого А1С1 = АС, В1С1 = ВС. 3). В треугольнике А1В1С1 по теореме Пифагора (А1В1)2 = (А1С1)2 + (В1С1)2. Следовательно (А1В1)2 = АС2 + ВС2. 4). Докажем равенство сторон АВ и А1В1.
5). Докажем равенство треугольников D АВС и D А1В1С1.
Билет № 21 4. Теорема синусов. Следствие из теоремы. 5. Доказательство теорем об углах, образованных пересекающимися хордами и секущими, проведенными из одной точки к окружности. Способ 1. Рассмотрим D
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.79.70 (0.204 с.) |
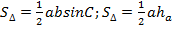 .
.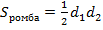 .
.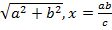 .
.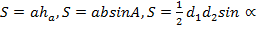 .
.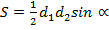 . Частный случай, если диагонали взаимно перпендикулярны.
. Частный случай, если диагонали взаимно перпендикулярны.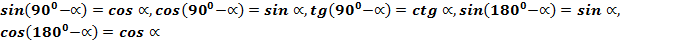 .
.

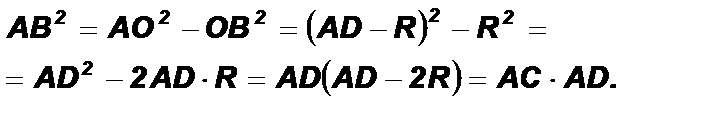
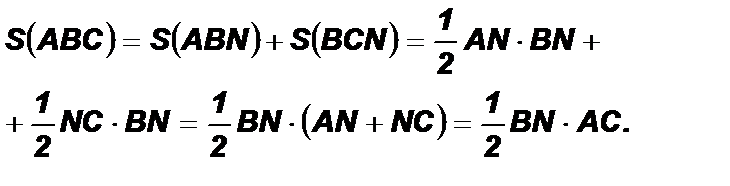
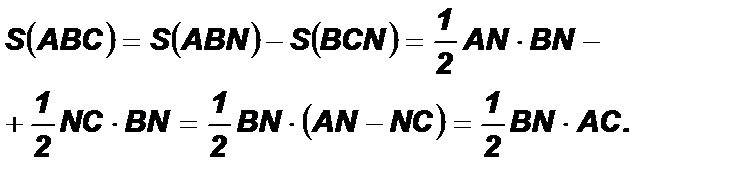

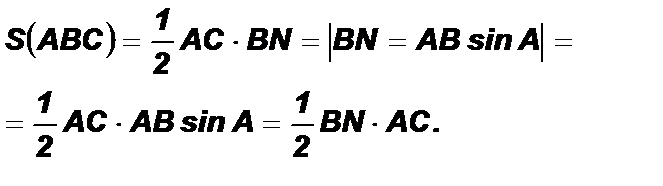
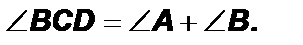

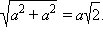 Поэтому
Поэтому 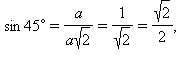
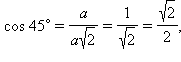
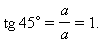
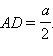 По теореме Пифагора
По теореме Пифагора 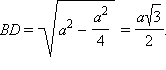 Значит:
Значит: 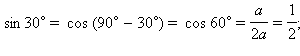
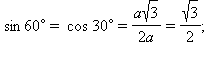
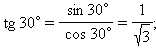
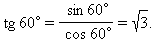


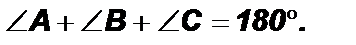
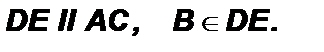

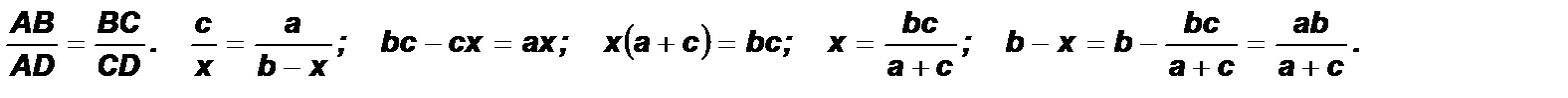
 В D = {О}; BO = OD; AO = OC.
В D = {О}; BO = OD; AO = OC.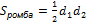 .
. .
.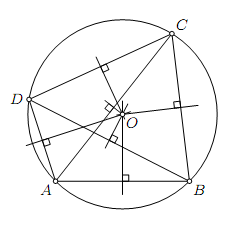 Другой критерий вписанного четырехугольника связан с его углами.
Другой критерий вписанного четырехугольника связан с его углами.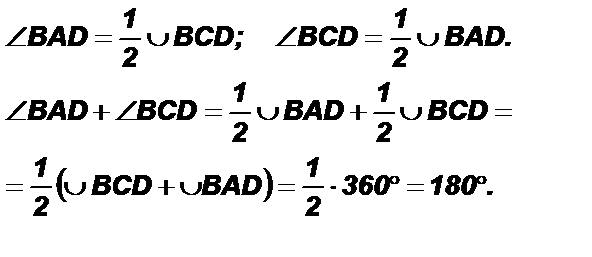
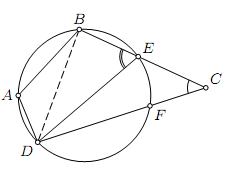 Достаточность. Пусть ∠ A + ∠ C = 180◦. Тогда эти углы не могут быть оба острыми или оба тупыми. Для определенности будем считать, что ∠ A > 90◦. Опишем около треугольника ABD окружность и докажем, что точка C ей принадлежит. Для этого необходимо опровергнуть два возможных
Достаточность. Пусть ∠ A + ∠ C = 180◦. Тогда эти углы не могут быть оба острыми или оба тупыми. Для определенности будем считать, что ∠ A > 90◦. Опишем около треугольника ABD окружность и докажем, что точка C ей принадлежит. Для этого необходимо опровергнуть два возможных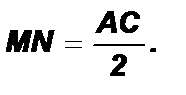
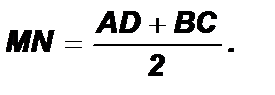
 .
.