
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные векторы матриц. Собственные числа матриц. Характеристическое уравнение. Базис определяемый собственными векторами матрицы. ⇐ ПредыдущаяСтр 9 из 9
Нахождение собственных чисел и собственных векторов матриц: Собственными числами матрицы Пусть столбец a - собственный вектор матрицы
Допустим, что определитель матрицыA – л E отличен от нуля, |A – л E|≠ 0. Тогда у этой матрицы существует обратная (A – л Е)^-1. Из равенства (А) получим, что а = (А – л Е)^-1 * 0 = 0, что противоречит определению собственного вектора. Значит, предположение, что | A – л Е| ≠ 0, неверно, то есть все собственные числа должны являться корнями уравнения|А –л Е| = 0.
Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A, если Av = λ v, где число λ называется собственным значением матрицы A. Таким образом преобразование, которое выполняет матрица A над вектором v, сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и α v — тоже собственный вектор.
Характеристическое уравнение матрицы — алгебраическое уравнение вида определитель, стоящий в левой части Х. у., получается из определителя матрицы А = || aik || n 1 вычитанием величины l из диагональных элементов. Этот определитель представляет собой многочлен относительно Х — характеристический многочлен. В раскрытом виде Х. у. записывается так: где S1 = a11 + a22 +... ann — т. н. след матрицы, S2 — сумма всех главных миноров 2-го порядка, т. е. миноров вида Базис, определяемый собственными векторами матрицы: Виды систем координат на плоскости. Уравнения связи декартовых и полярных координат. Примеры.
Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Виды систем: прямоугольная (декартова) система координат и полярная.
Полярная система координат задается т. О, называемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором e того же направления, что и луч Ор. Возьмем на плоскости т. М, не совпадающую с О. Положение т. М определяется двумя числами: ее расстоянием r от полюса О и углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24). Числа r и φ называются полярными координатами т. М, пишут М(r; φ), при этом r называют полярным радиусом, φ — полярным углом. Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком (-; ] (или 0< φ < 2r), а полярный радиус — [0;∞). В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно. Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось — с положительной полуосью Ох. Пусть x и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты. Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки
Полярные же координаты т. М выражаются через ее декартовы координаты (тот же рисунок) такими формулами
Определяя величину φ, следует установить (по знакам x и у) четверть, в которой лежит искомый угол, и учитывать, что - < φ< .
28. Прямая на плоскости. Виды задания прямой на плоскости. Взаимное расположение прямых на плоскости. Общее уравнение прямой на плоскости в декартовых координатах: Ах+Ву+С=0, где A, B и C — произвольные постоянные, причем A и B не равны 0 одновременно Способы задания прямой: 1)Задание с помощью зависимости у=у(х). 2)Параметрическое задание: х=х(t), у=у(t), где t-параметр. 3)Векторное задание r =r(t), где t- параметр. Прямые на плоскости: 1) у=kx+b – уравнение прямой с угловым коэффициентом k. 2)общее уравнение прямой Ах+Ву+С=0. 3) уравнение прямой, проходящей через данную точку в данном направлении: y-yo=k(x-xo). 4)уравнение прямой, проходящей через две точки: Частные случаи расположения прямой: 1)если прямая проходит через начало координат, то b=0; 2) если прямая параллельна оси Ох, то у=b; 3) если прямая параллельна оси Оу, то х=const.
29.Прямая на плоскости. Угол между прямыми. Условие параллельности и перпендикулярности. Общее уравнение прямой на плоскости в декартовых координатах: Ах+Ву+С=0, где A, B и C — произвольные постоянные, причем A и B не равны 0 одновременно. Угол между прямыми можно вычислить: I. Пусть прямые заданы с помощью ур-ий с угл. коэф. l1: y=k1x+b1; l2: y=k2x+b2 tg=(k2-k1)/(1+k2*k1) è1) если k1= k2, то прямые параллельны; 2)если k2k1= -1, то прямые перпендикулярны; 3)если k1≠k2, то прямые пересекаются II. Пусть прямые заданы с помощью общих уравнений:
tg=(А1В2-А2В1)/(А1А2-В1В2) è 1)если А1В2= А2В1, то прямые параллельны; 2) если А1/А2= В1/В2=С1/С2, то прямые совпадают; 3) если А1А2+В1В2=0, то прямые перпендикулярны; 4) если А1В2≠А2В1, то прямые пересекаются. 30.Прямая на плоскости. Угол между прямыми. Расстояние от точки до прямой. Общее уравнение прямой на плоскости в декартовых координатах: Ах+Ву+С=0. Угол между прямыми tg=(А1В2-А2В1)/(А1А2-В1В2) Уравнение прямой с угловым коэф. у=kx+b. Угол между прямыми tg=(k2-k1)/(1+k2*k1). Расстоянием от точки до прямой называется перпендикуляр опущенный из этой точки на данную прямую. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1: Либо такая формула
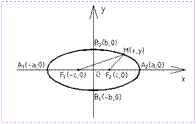
31.Кривые второго порядка. Канонические уравнения, графики, определения. Кривая называется кривой (линией) второго порядка, если она определяется уравнением второй степени относительно текущих координат х и у, т.е. уравнением вида Аx2 + 2Вxy + Сy2 + 2Dx + 2Еy + F = 0. К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола. 1) Окружностью радиуса R с центром в т. М0(х0;у0) наз-ся множество всех таких точек пл-ти М, что расстояние М0М всегда одно и то же и равно R. Каноническое уравнение (x – х0)2 + (y – у0)2 = R2 2) Эллипсом наз-ся множество всех точек на пл-ти, сумма расстояний от каждой из которых до двух данных точек этой пл-ти, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Канонич.ур-е эллипса
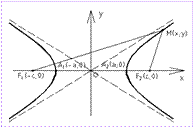
3) Гиперболой наз-ся множество всех точек пл-ти, модуль разности расстояний от каждой до двух данных точек пл-ти, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. Канонич. ур-е гиперболы:
4) Параболой наз-ся множество всех точек пл-ти, каждая из которых одинаково удалена от данной точки, называемой фокусом и данной прямой, называемой директрисой. Расстояние от фокуса до директрисы наз-ся параметром параболы и обозн-ся р. Канонич. ур-е параболы у2=2рх (парабола симметрична оси Ох) х2=2ру (симметрична оси Оу) у2= -2рх (имеет фокус F(р/2;0) и директрису х= -р/2) х2= -2ру (имеет фокус F(0;р/2) и директрису у= -р/2
32.Плоскость в трехмерном пространстве. Виды задания пл-тей.
Виды: 1. Ур-ие плоскости проходящий через данную точку перпендикулярен заданному вектору. A(x-x̥)+ B(y-y̥)+ C(z-z̥)=0 2. Общее ур-ие плоскости Ax + By +Cz +D=0 Частные случаи: 1 D=0, пл-ть проходит через начало координат. 2 С=0, Oz и пл-ть параллельны 3 С= D=0 проходит через ось Oz 4 А=В=0 пл-ть параллельна пл-ти Oxy 5 А=В=D=0 пл-ть совпадает с пл-тью Oxy 3. Ур-ие пл-ти в отрезках x/a + y/b + z/c =1 нормальное ур-ие пл-ти xcos+ ycos + zcosµ –p=0
|
|||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.2.15 (0.016 с.) |
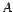 являются корни уравнения|А- λE| = 0и только они.
являются корни уравнения|А- λE| = 0и только они. с собственным числом
с собственным числом 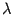 . Тогда, по определению,
. Тогда, по определению,  . Это равенство можно переписать в видеАа – л а = 0. Так как для единичной матрицы
. Это равенство можно переписать в видеАа – л а = 0. Так как для единичной матрицы 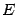 выполнено
выполнено 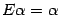 , то Аa –λEa = 0. По свойству матричного умножения (A –λE)a = Aa–λEa и предыдущее равенство принимает вид
, то Аa –λEa = 0. По свойству матричного умножения (A –λE)a = Aa–λEa и предыдущее равенство принимает вид

 ;
;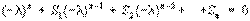 ,
, (i < k) и т.д., а S n — определитель матрицы А. Корни Х. у. l1, l2,..., l n называются собственными значениями матрицы А. У действительной симметричной матрицы, а также у эрмитовой матрицы все l k действительны, у действительной кососимметричной матрицы все l k чистомнимые числа; в случае действительной ортогональной матрицы, а также унитарной матрицы все |l k | = 1.
(i < k) и т.д., а S n — определитель матрицы А. Корни Х. у. l1, l2,..., l n называются собственными значениями матрицы А. У действительной симметричной матрицы, а также у эрмитовой матрицы все l k действительны, у действительной кососимметричной матрицы все l k чистомнимые числа; в случае действительной ортогональной матрицы, а также унитарной матрицы все |l k | = 1.
 Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми — осями, масштабом осей. Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу).(рис.23). Единичные векторы осей обозначают i и j (| i |=| j |=1). Систему координат обозначают Оху, а плоскость, в которой она расположена, называют координатной плоскость. Рассмотрим произвольную т.М пл-ти Оху. Вектор ОМ называется радиусом-вектором т.М. Если ОМ=(x;y), то координаты т. Μ записывают так: М(х;у). Эти два числа x и y полностью определяют положение точки на плоскости.
Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми — осями, масштабом осей. Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу).(рис.23). Единичные векторы осей обозначают i и j (| i |=| j |=1). Систему координат обозначают Оху, а плоскость, в которой она расположена, называют координатной плоскость. Рассмотрим произвольную т.М пл-ти Оху. Вектор ОМ называется радиусом-вектором т.М. Если ОМ=(x;y), то координаты т. Μ записывают так: М(х;у). Эти два числа x и y полностью определяют положение точки на плоскости. следующим образом:
следующим образом: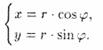
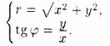
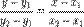 . Если х1=х2, то урав-е имеет вид х=х1. Если у1=у2 уравнение прямой примет вид у=у1. 5)уравнение прямой в отрезках
. Если х1=х2, то урав-е имеет вид х=х1. Если у1=у2 уравнение прямой примет вид у=у1. 5)уравнение прямой в отрезках 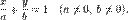 . 6)уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору А(х-х0)+В(у-у0)=0.
. 6)уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору А(х-х0)+В(у-у0)=0.
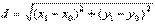 .
.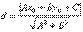



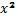 +
+  +
+ 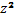 =1
=1


