
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение векторовСодержание книги
Поиск на нашем сайте
Определение 15.1. Скалярным произведением двух векторов Скалярное произведение будем обозначать
где Перечислим основные свойства скалярного произведения, разделив их на свойства алгебраические и геометрические. Алгебраические свойства. 1. Для любых векторов
т.е. скалярное произведение векторов обладает свойством коммутативности. Это свойство непосредственно следует из определения скалярного произведения. 2. Для любого числа
т.е. скалярный множитель можно выносить за знак скалярного произведения. Доказательство. Обозначим через
Если число
Наконец, если число 3. Для любых векторов
Доказательство. Обозначим через
Учитывая формулу
Геометрические свойства. 4. Скалярный квадрат вектора равен квадрату его длины, т.е.
В частности, Следует из определения скалярного произведения векторов и того факта, что 5. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перпендикулярны или хотя бы один из них нулевой. Доказательство. Действительно
6. Скалярное произведение двух ненулевых векторов положительно (отрицательно) тогда и только тогда, когда угол между ними острый (тупой). Доказательство. Действительно знак скалярного произведения ненулевых векторов, согласно определению, совпадает со знаком косинуса угла между ними. Координатная форма скалярного произведения ТЕОРЕМА 16.1. Пусть в пространстве выбран ортонормированный базис
где
|
|||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 108; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.217.176 (0.008 с.) |

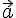 и
и 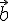 называется число, равное произведению длин этих векторов на косинус угла между ними.
называется число, равное произведению длин этих векторов на косинус угла между ними.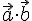 или просто
или просто 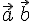 . По определению имеем
. По определению имеем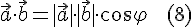
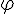 --- угол между векторами
--- угол между векторами 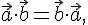
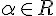 и любых векторов
и любых векторов 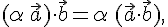
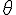 угол между вектором
угол между вектором 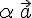 и
и 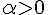 и векторы ненулевые, то
и векторы ненулевые, то 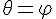 и мы получаем (см.рис. 1)
и мы получаем (см.рис. 1)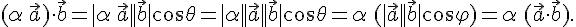
 и векторы ненулевые, то
и векторы ненулевые, то 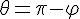 и мы получаем (см.рис. 2)
и мы получаем (см.рис. 2)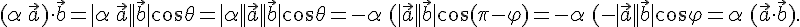
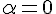 или один из векторов нулевой, то доказываемое равенство очевидно.
или один из векторов нулевой, то доказываемое равенство очевидно.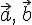 и
и 
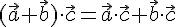
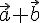 и
и 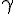 угол между вектором
угол между вектором 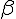 угол между вектором
угол между вектором 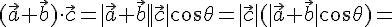
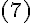 и свойство 2. проекций векторов, имеем
и свойство 2. проекций векторов, имеем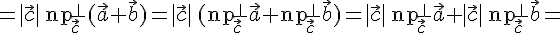
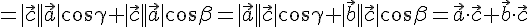
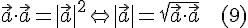
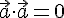 тогда и только тогда, когда вектор
тогда и только тогда, когда вектор 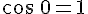 .
. или
или 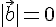 или
или 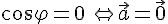 или
или 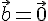 или
или 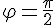 .
.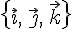 , в котором
, в котором 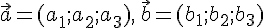 . Тогда
. Тогда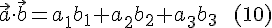
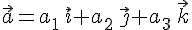 и
и 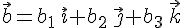 , поэтому
, поэтому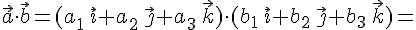
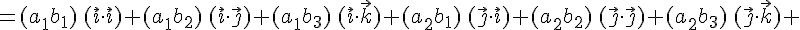
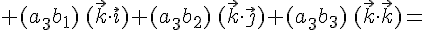
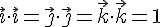 и
и 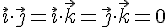 , значит, окончательно получим
, значит, окончательно получим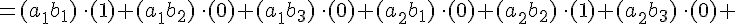
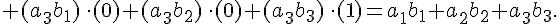
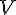 ), то формула
), то формула 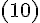 принимает вид
принимает вид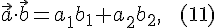
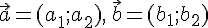 в ортонормированном базисе двумерного подпространства
в ортонормированном базисе двумерного подпространства 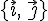 .
.


