
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базис векторного пространства. Координаты вектора.
Определение 10.1. Базисом векторного пространства 1. Система данных векторов линейно независима. 2. Любой вектор пространства
Определение 10.2. Коэффициенты разложения В этом случае мы будем писать Рассмотрим теперь векторное пространство ТЕОРЕМА 10.1. Любая упорядоченная система трех некомпланарных векторов пространства Доказательство. По следствию 9.2. такая система векторов линейно независима, а по теореме 7.2. любой вектор пространства ТЕОРЕМА 10.2. Любой базис пространства состоит из трех векторов. Доказательство. Пусть Определение 10.3. Число векторов в любом базисе называется размерностью векторного пространства. Таким образом, размерность векторного пространства Различают два вида базисов. 1. Аффинный --- базисные векторы имеют произвольную длину и углы между ними любые. Произвольный аффинный базис мы будем обозначать 2. Ортонормированный или декартов базис, частный случай аффинного базиса. Этот базис будем обозначать Замечание 10.1. Поскольку ортонормированный базис есть частный случай аффинного, то всё, что доказано для аффинных базисов справедливо и для ортонормированных, но не наоборот. Свойства координат вектора.
ТЕОРЕМА 10.3. Пусть
Доказательство. По определению координат вектора имеем:
Поэтому вектор Используя свойства операций умножения вектора на число и сложения векторов, раскроем скобки и получим
Последнее равенство по определению означает, что
Из теоремы 10.3. получаем следующие следствия. Следствие 10.1. Любая координата суммы (разности) векторов равна сумме (разности) соответствующих координат этих векторов. Следствие 10.2. При умножении вектора на число каждая координата умножается на это число. Следствие 10.3. Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны. Векторные подпространства Определение 11.1. Пусть 2. Если По аналогии с пространством Пусть теперь имеем дело с пространством 1. Возьмем два неколлинеарных вектора
где Это множество, как нетрудно проверить, удовлетворяет обоим условиям определения векторного подпространства, поэтому является подпространством пространства
Векторы 2. Возьмем ненулевой вектор
где Вектор 3. Рассмотрим множество, состоящее только из одного нулевого вектора. Оно удовлетворяет обоим условиям определения векторного подпространства, поэтому является подпространством пространства
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.27.178 (0.014 с.) |
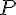 называется такая упорядоченная система векторов
называется такая упорядоченная система векторов 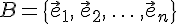 , которая удовлетворяет следующим требованиям:
, которая удовлетворяет следующим требованиям: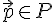 является линейной комбинацией данной системы векторов, т.е.
является линейной комбинацией данной системы векторов, т.е.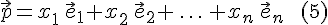
 в виде линейной комбинации векторов базиса однозначно.
в виде линейной комбинации векторов базиса однозначно.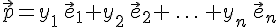 , то получим равенство
, то получим равенство
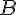 линейно независима, то все числа
линейно независима, то все числа 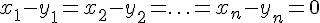 .
.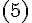 называются координатами вектора
называются координатами вектора 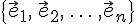 .
. .
.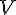 . Докажем несколько теорем о базисе пространства
. Докажем несколько теорем о базисе пространства 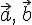 , а вектор
, а вектор  такой, что
такой, что 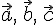 --- некомпланарны, то по следствию 9.2.
--- некомпланарны, то по следствию 9.2. 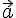 и
и 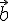 . Тем более один вектор не может служить базисом пространства
. Тем более один вектор не может служить базисом пространства 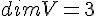 .
. .
.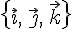 , базисные векторы этого базиса единичные и взаимно перпендикулярные
, базисные векторы этого базиса единичные и взаимно перпендикулярные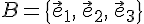 --- базис пространства
--- базис пространства 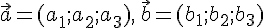 . Тогда для любых действительных чисел
. Тогда для любых действительных чисел 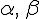 вектор
вектор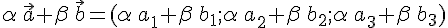
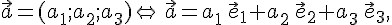
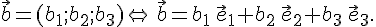
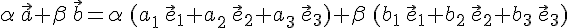


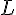 --- непустое множество векторов из векторного пространства
--- непустое множество векторов из векторного пространства 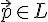 и
и  , то
, то  .
.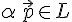 для любого вещественного числа
для любого вещественного числа 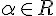 .
.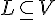 , а в
, а в 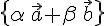 ,
,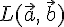 . Пусть
. Пусть 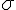 --- плоскость, которой параллельны векторы
--- плоскость, которой параллельны векторы 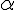 и
и 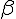 векторы
векторы 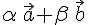 линейно зависимы, поэтому они компланарны, то есть вектор
линейно зависимы, поэтому они компланарны, то есть вектор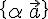 ,
,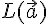 . Пусть
. Пусть 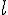 --- прямая, которой параллелен вектор
--- прямая, которой параллелен вектор 


