Направленные отрезки
Определение 1.1. Отрезок называется направленным (сокращенно НО), если учитывается порядок задания его концов.
Пусть 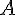 и
и 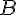 — концы НО.
— концы НО. 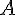 — первый — начало НО,
— первый — начало НО, 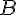 — второй — конец НО. Будем обозначать через
— второй — конец НО. Будем обозначать через 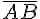 направленный отрезок с концами
направленный отрезок с концами 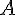 и
и 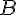 . Если концы
. Если концы 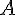 и
и 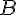 совпадают, то НО называется нулевым или вырожденным и мы пишем
совпадают, то НО называется нулевым или вырожденным и мы пишем  или
или  .
.
Определение 1.2. Длиной направленного отрезка 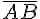 будем называть длину соответствующего обычного отрезка. Длину направленного отрезка будем обозначать через
будем называть длину соответствующего обычного отрезка. Длину направленного отрезка будем обозначать через 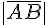 . В частности,
. В частности, 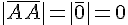 .
.
Определение 1.3. Два невырожденных направленных отрезка 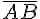 и
и 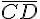 называются коллинеарными,если прямые
называются коллинеарными,если прямые 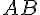 и
и 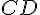 или параллельны, или совпадают. Вырожденный направленный отрезок считается коллинеарным любому направленному отрезку.
или параллельны, или совпадают. Вырожденный направленный отрезок считается коллинеарным любому направленному отрезку.
Коллинеарные отрезки обозначаются 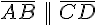 .
.
Определение 1.4. Будем говорить, что два невырожденных направленных отрезка 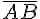 и
и 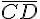 , лежащих на параллельных прямых, имеют одинаковое (противоположное) направление, если точки
, лежащих на параллельных прямых, имеют одинаковое (противоположное) направление, если точки 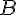 и
и 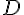 лежат по одну (по разные) стороны от прямой
лежат по одну (по разные) стороны от прямой 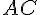 .
.
Определение 1.5. В случае, если невырожденные направленные отрезки 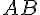 и
и 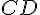 лежат на одной прямой
лежат на одной прямой 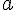 , они имеют одинаковое направление, если на любой прямой
, они имеют одинаковое направление, если на любой прямой 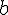 , параллельной
, параллельной 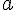 найдется невырожденный направленный отрезок
найдется невырожденный направленный отрезок 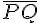 , имеющий одинаковое направление с каждым из направленных отрезков
, имеющий одинаковое направление с каждым из направленных отрезков 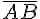 и
и 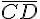 . Если же любой невырожденный отрезок
. Если же любой невырожденный отрезок 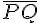 (лежащий на прямой
(лежащий на прямой 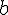 , параллельной прямой
, параллельной прямой 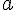 ) имеет одинаковое направление с одним из отрезков
) имеет одинаковое направление с одним из отрезков 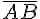 и
и 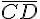 и противоположное сдругим, то направленные отрезки
и противоположное сдругим, то направленные отрезки 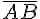 и
и 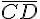 имеют противоположное направление.
имеют противоположное направление.
Условимся считать, что вырожденный направленный отрезок имеет одинаковое направление с любым напраленным отрезком. Одинаково направленные (сонаправленные)отрезки обозначаются 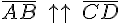 , а противоположно направленные
, а противоположно направленные 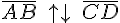 .
.
Определение 1.6. Два направленных отрезка 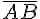 и
и 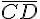 называются эквиполентными, если
называются эквиполентными, если
1) 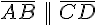 ;
;
2) 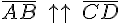 ;
;
3) 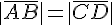 .
.
Эквиполентные направленные отрезки мы обозначаем  .
.
ЛЕММА 1.1. (признак эквиполентности направленных отрезков)
Необходимым и достаточным условием эквиполентности направленных отрезков 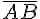 и
и 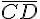 является совпадение середины отрезка
является совпадение середины отрезка 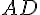 с серединой отрезка
с серединой отрезка 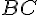 .
.
Доказательство необходимости. Дано  .Пусть
.Пусть 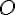 — середина отрезка
— середина отрезка 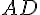 . Рассмотрим центральную симметрию
. Рассмотрим центральную симметрию 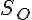 относительно точки
относительно точки 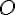 . Совершенно очевидно, что каждый направленный отрезок
. Совершенно очевидно, что каждый направленный отрезок 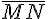 при центральной симметрии переходит в направленный отрезок
при центральной симметрии переходит в направленный отрезок 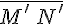 , такой, что
, такой, что 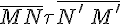 . Пусть
. Пусть 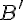 — точка, в которую при преобразовании
— точка, в которую при преобразовании 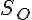 перейдет точка
перейдет точка 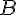 . Так как точка
. Так как точка 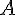 переходит в точку
переходит в точку 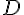 , то направленный отрезок
, то направленный отрезок 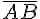 перейдет в направленный отрезок
перейдет в направленный отрезок 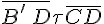 и, значит, точки
и, значит, точки 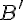 и
и 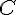 совпадают, т.е. точка
совпадают, т.е. точка 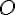 является также и серединой отрезка
является также и серединой отрезка 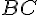 .
.
Доказательство достаточности. Предположим, что середина отрезка 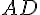 совпадает с серединой отрезка
совпадает с серединой отрезка 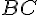 . Обозначим их общую середину через
. Обозначим их общую середину через 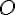 . Значит при преобразовании
. Значит при преобразовании 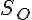 симметрии относительно точки
симметрии относительно точки 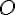 точка
точка 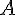 перейдет в точку
перейдет в точку 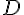 , а точка
, а точка 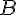 перейдет в точку
перейдет в точку 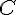 , поэтому
, поэтому  .
.
Понятие вектора
Сложение векторов
Определение 3.1. Суммой двух векторов  и
и 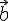 называется вектор
называется вектор 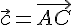 , где
, где 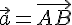 ,
, 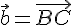 ,
, 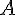 — произвольная точка,
— произвольная точка, 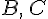 — точки, полученные после откладывания векторов
— точки, полученные после откладывания векторов  и
и 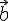 .
.
Покажем, что сумма векторов не зависит от выбора точки 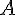 .
.
Действительно, пусть 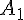 --- любая точка, отличная от точки
--- любая точка, отличная от точки 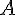 . Строим векторы
. Строим векторы 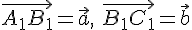 . Докажем, что
. Докажем, что 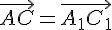 .
.
Так как 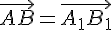 и
и 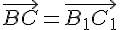 , то по лемме2.1.
, то по лемме2.1. 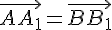 и
и  , то есть
, то есть 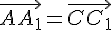 . Следовательно, по той же лемме
. Следовательно, по той же лемме
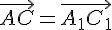 .
.
Замечание 3.1. Для нахождения суммы неколлинеарных векторов приходится строить треугольник 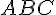 . Поэтому правило сложения векторов называется правилом треугольника. Из этого правила следует, что для любых трех точек
. Поэтому правило сложения векторов называется правилом треугольника. Из этого правила следует, что для любых трех точек 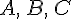 справедливо равенство
справедливо равенство
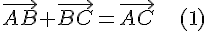
В частности, это правило справедливо и для коллинеарных точек.
Свойства сложения векторов.
ТЕОРЕМА 3.1. Для произвольных векторов 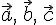 справедливы следующие равенства:
справедливы следующие равенства:
1. 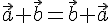 --- коммутативность сложения векторов.
--- коммутативность сложения векторов.
2. 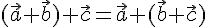 --- ассоциативность сложения векторов.
--- ассоциативность сложения векторов.
3. 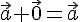 .
.
4. 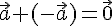 .
.
Доказательство.
1. Пусть  и
и 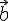 --- произвольные векторы. От какой-нибудь точки
--- произвольные векторы. От какой-нибудь точки 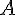 отложим векторы
отложим векторы 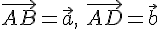 , а затем от точки
, а затем от точки 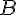 отложим вектор
отложим вектор 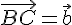 . Согласно построению
. Согласно построению 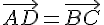 , поэтому по лемме 2.1. получаем
, поэтому по лемме 2.1. получаем 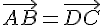 , т.е.
, т.е. 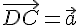 .
.
По правилу треугольника 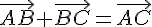 и
и 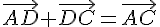 , следовательно,
, следовательно, 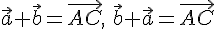 . Отсюда получаем, что
. Отсюда получаем, что 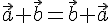 .
.
2. Пусть 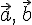 и
и  --- произвольные векторы. Возьмем какую-нибудь точку
--- произвольные векторы. Возьмем какую-нибудь точку  и отложим последовательно векторы
и отложим последовательно векторы
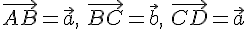 .
.
По правилу треугольника 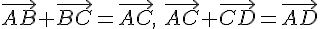 , поэтому
, поэтому 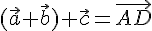 . С другой стороны
. С другой стороны  , поэтому
, поэтому 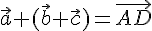 . Отсюда получаем требуемое.
. Отсюда получаем требуемое.
3. Применим правило 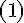 к точкам
к точкам 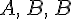 получим
получим
 .
.
Значит, 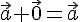 .
.
4. Применим правило  к точкам
к точкам 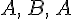 получим
получим
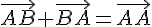 .
.
Значит, 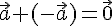 .
.
Замечание 3.2.
1. Суммой векторов 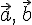 и
и  будем считать вектор
будем считать вектор 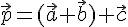 . На основании доказанной теоремы
. На основании доказанной теоремы 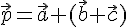 , поэтому при записи суммы трех векторов можно опустить скобки и писать просто
, поэтому при записи суммы трех векторов можно опустить скобки и писать просто  . Более того, можно доказать, что сумма трех векторов не зависит от порядка слагаемых. В самом деле, докажем, например, что
. Более того, можно доказать, что сумма трех векторов не зависит от порядка слагаемых. В самом деле, докажем, например, что
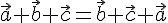 :
:
 .
.
2. Аналогично можно определить сумму 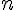 векторов, где
векторов, где 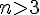 . Пусть
. Пусть 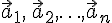 --- произвольные векторы. Их суммой называется вектор
--- произвольные векторы. Их суммой называется вектор 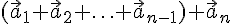 , и обозначается так:
, и обозначается так: 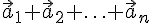 .
.
Из второго свойства можно получить правило многоугольника для нахождения суммы любого конечного числа векторов. Оно таково:
Суммой конечного числа векторов называется вектор, идущий из начала первого в конец последнего, при условии, что каждый последующий вектор отложен из конца предыдущего.
Нетрудно убедиться в том, что сумма 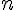 векторов не зависит от порядка слагаемых.
векторов не зависит от порядка слагаемых.
3. Для неколлинеарных векторов при их сложении можно пользоваться правилом параллелограмма:
Суммой двух неколлинеарных векторов является диагональ параллелограмма, построенного на этих векторах как на сторонах, при условии, что начало искомого вектора совпадает с началом данных векторов.
Разность векторов.
Определение 4.1. Разностью векторов  и
и 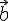 , взятых в данном порядке, называется такой вектор
, взятых в данном порядке, называется такой вектор 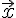 , который в сумме со вторым вектором дает первый вектор.
, который в сумме со вторым вектором дает первый вектор.
Докажем существование и единственность разности.
Существование. Отложим векторы  и
и 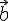 от одной и той же точки
от одной и той же точки 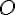 :
:
Применяя равенство 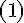 для точек
для точек 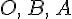 получаем
получаем
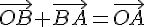
Полагая 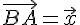 , будем иметь
, будем иметь 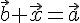 . Этим доказано существование разности.
. Этим доказано существование разности.
Единственность. Пусть существует еще вектор  такой, что
такой, что 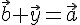 . Тогда
. Тогда 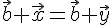 . Прибавим к обеим частям этого равенства вектор
. Прибавим к обеим частям этого равенства вектор 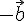 . Получим
. Получим
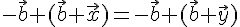
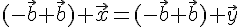
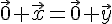
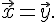
Таким образом, доказано существование и единственность разности любых двух векторов, при этом эта разность обозначается 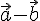 .
.
Замечание 4.1. Из доказательства существования разности векторов можно сформулировать правило нахождения разности двух векторов:
Разностью двух данных векторов, отложенных из одной точки является вектор, идущий из конца второго в конец первого.
Отметим еще равенство
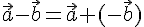
В самом деле,

Умножение вектора на число.
Определение 5.1. Произведением вектора 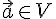 на действительное число
на действительное число 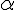 называется вектор
называется вектор 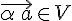 , который удовлетворяет двум условиям:
, который удовлетворяет двум условиям:
1. 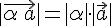 ;
;
2. 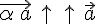 , если
, если 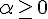 и
и
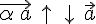 , если
, если  .
.
Из условия 1. следует, что 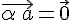 тогда и только тогда, когда
тогда и только тогда, когда 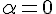 или
или  .
.
В дальнейшем вместо записи 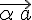 будем употреблять запись
будем употреблять запись 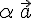
Напомним определение гомотетии, известное из школьного курса геометрии.
Определение 5.2. Гомотетией с центром в точке 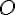 и коэффициентом
и коэффициентом 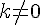 называется такое преобразование плоскости, при котором каждой точке
называется такое преобразование плоскости, при котором каждой точке 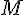 ставится в соответствие точка
ставится в соответствие точка 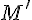 такая, что выполнены следующие условия:
такая, что выполнены следующие условия:
1. точки  лежат на одной прямой;
лежат на одной прямой;
2. 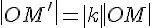 ;
;
3. 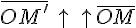 , если
, если 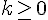 и
и
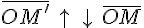 , если
, если 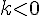 .
.
Предварительно докажем одну лемму.
ЛЕММА 5.1. Если при гомотетии с центром в точке 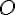 и коэффициентом
и коэффициентом 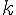 треугольник
треугольник 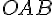 переходит
переходит
в треугольник 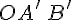 , то
, то  .
.
Доказательство. По определению гомотетии имеем 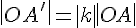 и
и 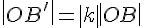 , поэтому
, поэтому 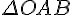 подобен
подобен 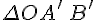 с коэффициентом
с коэффициентом 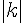 . Отсюда следует, что
. Отсюда следует, что 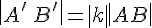 и
и 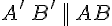 . Если
. Если 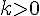 , то точки
, то точки 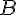 и
и 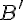 лежат по одну сторону от прямой
лежат по одну сторону от прямой 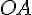 , поэтому
, поэтому 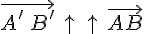 , следовательно,
, следовательно,  . Если
. Если 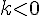 , то точки
, то точки 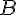 и
и 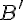 лежат по разные стороны от прямой
лежат по разные стороны от прямой 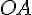 , поэтому
, поэтому 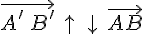 , т.е. и в этом случае
, т.е. и в этом случае  .
.
Свойства координат вектора.
ТЕОРЕМА 10.3. Пусть 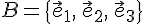 --- базис пространства
--- базис пространства 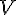 и пусть в этом базисе векторы
и пусть в этом базисе векторы 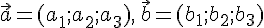 . Тогда для любых действительных чисел
. Тогда для любых действительных чисел 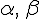 вектор
вектор
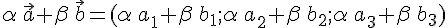
в базисе 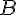 .
.
Доказательство. По определению координат вектора имеем:
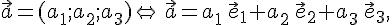
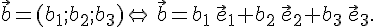
Поэтому вектор
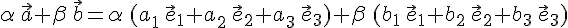
Используя свойства операций умножения вектора на число и сложения векторов, раскроем скобки и получим


Последнее равенство по определению означает, что
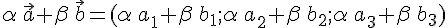
в базисе 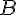 .
.
Из теоремы 10.3. получаем следующие следствия.
Следствие 10.1. Любая координата суммы (разности) векторов равна сумме (разности) соответствующих координат этих векторов.
Следствие 10.2. При умножении вектора на число каждая координата умножается на это число.
Следствие 10.3. Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны.
Векторные подпространства
Определение 11.1. Пусть 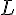 --- непустое множество векторов из векторного пространства
--- непустое множество векторов из векторного пространства 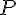 . Множество
. Множество 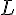 называется векторным подпространством пространства
называется векторным подпространством пространства 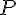 , если выполнены следующие два условия:
, если выполнены следующие два условия:
1. Если 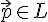 и
и  , то
, то  .
.
2. Если 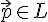 , то
, то 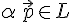 для любого вещественного числа
для любого вещественного числа 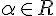 .
.
По аналогии с пространством 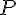 введем понятие базиса подпространства
введем понятие базиса подпространства 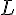 . Базисом векторного подпространства
. Базисом векторного подпространства 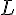 называется такая упорядоченная система линейно независимых векторов из
называется такая упорядоченная система линейно независимых векторов из 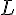 , что любой вектор подпространства
, что любой вектор подпространства 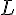 является линейной комбинацией данной системы векторов. Можно доказать, что все базисы подпространства
является линейной комбинацией данной системы векторов. Можно доказать, что все базисы подпространства 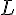 состоят из одного и того же числа векторов. Это число называется размерностью векторного подпространства.
состоят из одного и того же числа векторов. Это число называется размерностью векторного подпространства.
Пусть теперь имеем дело с пространством 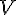 . Так как
. Так как 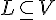 , а в
, а в 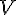 любая система, состоящая более чем из трех векторов линейно зависима, то размерность любого подпространства пространства
любая система, состоящая более чем из трех векторов линейно зависима, то размерность любого подпространства пространства 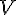 не больше, чем три.
не больше, чем три.
Рассмотрим примеры векторных подпространств пространства 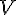 и выясним их геометрический смысл.
и выясним их геометрический смысл.
1. Возьмем два неколлинеарных вектора  и
и 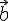 пространства
пространства 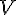 и рассмотрим множество всех векторов вида:
и рассмотрим множество всех векторов вида:
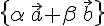 ,
,
где 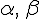 --- произвольные действительные числа.
--- произвольные действительные числа.
Это множество, как нетрудно проверить, удовлетворяет обоим условиям определения векторного подпространства, поэтому является подпространством пространства 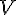 . Оно называется подпространством натянутым на векторы
. Оно называется подпространством натянутым на векторы  и
и 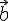 , и обозначается
, и обозначается 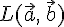 . Пусть
. Пусть 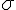 --- плоскость, которой параллельны векторы
--- плоскость, которой параллельны векторы  и
и 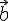 . Докажем, что
. Докажем, что 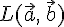 --- множество тех и только тех векторов пространства
--- множество тех и только тех векторов пространства 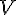 , которые параллельны плоскости
, которые параллельны плоскости 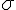 . Действительно, при любых значениях
. Действительно, при любых значениях 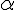 и
и 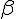 векторы
векторы 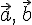 и
и 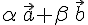 линейно зависимы, поэтому они компланарны, то есть вектор
линейно зависимы, поэтому они компланарны, то есть вектор
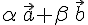 параллелен плоскости
параллелен плоскости 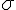 . Обратно, любой вектор
. Обратно, любой вектор  , параллельный плоскости
, параллельный плоскости 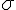 , компланарен с векторами
, компланарен с векторами  и
и 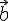 , поэтому является линейной комбинацией векторов
, поэтому является линейной комбинацией векторов  и
и 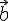 , то есть принадлежит множеству
, то есть принадлежит множеству 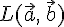 .
.
Векторы  и
и 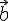 образуют базис подпространства
образуют базис подпространства 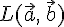 . В самом деле, эти векторы линейно независимы по следствию 9.1., и любой вектор подпространства
. В самом деле, эти векторы линейно независимы по следствию 9.1., и любой вектор подпространства 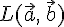 является линейной комбинацией векторов
является линейной комбинацией векторов  и
и 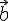 по построению этого множества. Таким образом, множество всех векторов,
по построению этого множества. Таким образом, множество всех векторов,
параллельных некоторой плоскости, является двумерным векторным подпространством пространства 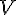 .
.
Еще раз отметим, что базисом такого подпространства является любая упорядоченная пара неколлинеарных векторов.
2. Возьмем ненулевой вектор  пространства
пространства 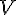 и рассмотрим множество всех векторов вида:
и рассмотрим множество всех векторов вида:
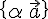 ,
,
где 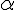 --- произвольное действительное число. Это множество является векторным подпространством пространства
--- произвольное действительное число. Это множество является векторным подпространством пространства 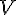 . Обозначим его через
. Обозначим его через 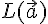 . Пусть
. Пусть 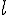 --- прямая, которой параллелен вектор
--- прямая, которой параллелен вектор  . Аналогично примеру 1 можно доказать, что
. Аналогично примеру 1 можно доказать, что 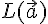 --- множество всех тех и только тех векторов пространства
--- множество всех тех и только тех векторов пространства 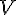 , которые параллельны прямой
, которые параллельны прямой 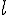 .
.
Вектор  является базисом подпространства
является базисом подпространства 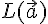 , поэтому
, поэтому 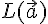 --- одномерное векторное подпространство. Таким образом, множество всех векторов, параллельных некоторой прямой, является одномерным векторным подпространством пространства
--- одномерное векторное подпространство. Таким образом, множество всех векторов, параллельных некоторой прямой, является одномерным векторным подпространством пространства 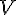 .
.
3. Рассмотрим множество, состоящее только из одного нулевого вектора. Оно удовлетворяет обоим условиям определения векторного подпространства, поэтому является подпространством пространства 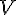 . Оно называется нулевым или тривиальным векторным подпространством. Принято считать, что размерность этого подпространства равна нулю.
. Оно называется нулевым или тривиальным векторным подпространством. Принято считать, что размерность этого подпространства равна нулю.
Проекция вектора на ось
Пусть 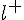 --- ось и
--- ось и 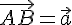 --- некоторый вектор. Обозначим через
--- некоторый вектор. Обозначим через 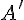 и
и 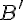 параллельные проекции точек
параллельные проекции точек 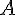 и
и 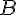 на прямую
на прямую 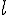 .
.
Определение 14.1. Проекцией вектора 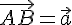 на ось
на ось 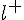 называется величина
называется величина 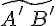 направленного отрезка
направленного отрезка 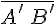 на оси.
на оси.
Замечание 14.1. Согласно определению 11.1. проекция вектора на ось --- это число, равное длине отрезка 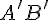 , взятое с определенным знаком.
, взятое с определенным знаком.
Проекцию вектора  на ось
на ось 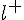 будем обозначать через
будем обозначать через 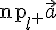 . В случае ортогонального проектирования применяется обозначение
. В случае ортогонального проектирования применяется обозначение 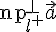 . Отметим, что
. Отметим, что
ортогональное проектирование есть частный случай параллельного, поэтому для него выполняются все свойства параллельного проектирования, но не наоборот.
Кроме того отметим, что проекцию вектора мы определили через проекцию его представителя, поэтому необходимо доказать, что это определение не зависит от выбора представителя. Это доказательство отнесем к свойствам
проекций векторов на ось.
Свойства проекций векторов на ось.
1. Проекции равных векторов равны.(более точно, проекции эквиполентных направленных отрезков равны)
Доказательство. Пусть 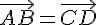 . Обозначим через:
. Обозначим через:
 проекции точек
проекции точек 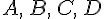 . Так как
. Так как 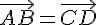 , то середины отрезков
, то середины отрезков 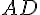 и
и 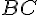 совпадают и, кроме того, при параллельном проектировании середина отрезка проектируется в
совпадают и, кроме того, при параллельном проектировании середина отрезка проектируется в
середину его проекции, следовательно середина отрезка  совпадает с серединой отрезка
совпадает с серединой отрезка  , значит,
, значит, 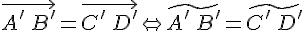 .
.
2. Проекция суммы векторов на ось есть сумма проекций слагаемых векторов, т.е.
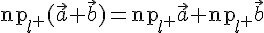
Доказательство. Пусть 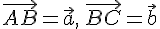 тогда
тогда
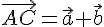 . Обозначим через:
. Обозначим через: 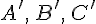 проекции точек
проекции точек 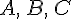 . Используя основное тождество (см. теорему 12.1.) для точек
. Используя основное тождество (см. теорему 12.1.) для точек 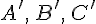 оси, получим
оси, получим
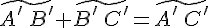 .
.
Для завершения доказательства достаточно заметить, что
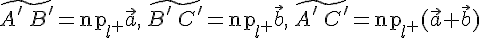 .
.
3. Для ортогональной проекции
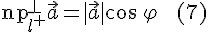
где 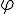 --- угол между вектором
--- угол между вектором  и осью.
и осью.
Доказательство. Пусть 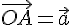 . Так как проекции равных векторов равны между собой, то можно считать, что вектор
. Так как проекции равных векторов равны между собой, то можно считать, что вектор 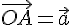 отложен от точки
отложен от точки  оси
оси  . Обозначим через
. Обозначим через 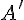 проекцию точки
проекцию точки 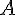 на ось. Если вектор
на ось. Если вектор  ненулевой и угол
ненулевой и угол 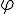 --- острый, то (см. рис. 1)
--- острый, то (см. рис. 1)

Если же вектор  ненулевой и угол
ненулевой и угол 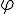 --- тупой, то (см. рис. 2)
--- тупой, то (см. рис. 2)
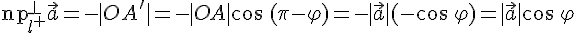
В случае когда вектор  или он перпендикулярен оси, формула
или он перпендикулярен оси, формула 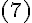 очевидна.
очевидна.
Геометрические свойства.
4. Скалярный квадрат вектора равен квадрату его длины, т.е.
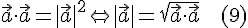
В частности, 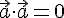 тогда и только тогда, когда вектор
тогда и только тогда, когда вектор  нулевой.
нулевой.
Следует из определения скалярного произведения векторов и того факта, что 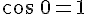 .
.
5. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перпендикулярны или хотя бы один из них нулевой.
Доказательство. Действительно
 или
или 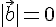 или
или 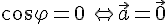 или
или 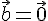 или
или 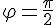 .
.
6. Скалярное произведение двух ненулевых векторов положительно (отрицательно) тогда и только тогда, когда угол между ними острый (тупой).
Доказательство. Действительно знак скалярного произведения ненулевых векторов, согласно определению, совпадает со знаком косинуса угла между ними.
Направленные отрезки
Определение 1.1. Отрезок называется направленным (сокращенно НО), если учитывается порядок задания его концов.
Пусть 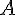 и
и 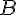 — концы НО.
— концы НО. 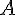 — первый — начало НО,
— первый — начало НО, 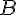 — второй — конец НО. Будем обозначать через
— второй — конец НО. Будем обозначать через 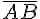 направленный отрезок с концами
направленный отрезок с концами 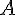 и
и 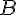 . Если концы
. Если концы 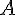 и
и 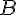 совпадают, то НО называется нулевым или вырожденным и мы пишем
совпадают, то НО называется нулевым или вырожденным и мы пишем  или
или  .
.
Определение 1.2. Длиной направленного отрезка 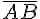 будем называть длину соответствующего обычного отрезка. Длину направленного отрезка будем обозначать через
будем называть длину соответствующего обычного отрезка. Длину направленного отрезка будем обозначать через 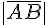 . В частности,
. В частности, 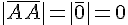 .
.
Определение 1.3. Два невырожденных направленных отрезка 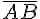 и
и 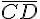 называются коллинеарными,если прямые
называются коллинеарными,если прямые 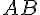 и
и 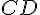 или параллельны, или совпадают. Вырожденный направленный отрезок считается коллинеарным любому направленному отрезку.
или параллельны, или совпадают. Вырожденный направленный отрезок считается коллинеарным любому направленному отрезку.
Коллинеарные отрезки обозначаются 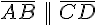 .
.
Определение 1.4. Будем говорить, что два невырожденных направленных отрезка 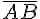 и
и 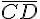 , лежащих на параллельных прямых, имеют одинаковое (противоположное) направление, если точки
, лежащих на параллельных прямых, имеют одинаковое (противоположное) направление, если точки 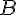 и
и 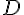 лежат по одну (по разные) стороны от прямой
лежат по одну (по разные) стороны от прямой 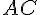 .
.
Определение 1.5. В случае, если невырожденные направленные отрезки 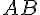 и
и 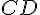 лежат на одной прямой
лежат на одной прямой 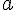 , они имеют одинаковое направление, если на любой прямой
, они имеют одинаковое направление, если на любой прямой 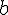 , параллельной
, параллельной 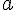 найдется невырожденный направленный отрезок
найдется невырожденный направленный отрезок 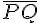 , имеющий одинаковое направление с каждым из направленных отрезков
, имеющий одинаковое направление с каждым из направленных отрезков 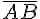 и
и 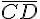 . Если же любой невырожденный отрезок
. Если же любой невырожденный отрезок 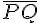 (лежащий
(лежащий


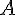 и
и 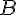 — концы НО.
— концы НО. 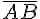 направленный отрезок с концами
направленный отрезок с концами  или
или  .
.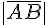 . В частности,
. В частности, 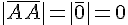 .
.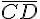 называются коллинеарными,если прямые
называются коллинеарными,если прямые 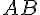 и
и 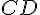 или параллельны, или совпадают. Вырожденный направленный отрезок считается коллинеарным любому направленному отрезку.
или параллельны, или совпадают. Вырожденный направленный отрезок считается коллинеарным любому направленному отрезку.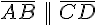 .
.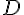 лежат по одну (по разные) стороны от прямой
лежат по одну (по разные) стороны от прямой 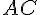 .
.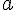 , они имеют одинаковое направление, если на любой прямой
, они имеют одинаковое направление, если на любой прямой 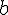 , параллельной
, параллельной 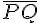 , имеющий одинаковое направление с каждым из направленных отрезков
, имеющий одинаковое направление с каждым из направленных отрезков 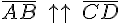 , а противоположно направленные
, а противоположно направленные 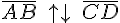 .
.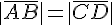 .
. .
.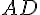 с серединой отрезка
с серединой отрезка 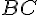 .
. — середина отрезка
— середина отрезка 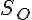 относительно точки
относительно точки 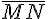 при центральной симметрии переходит в направленный отрезок
при центральной симметрии переходит в направленный отрезок 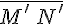 , такой, что
, такой, что 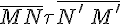 . Пусть
. Пусть 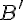 — точка, в которую при преобразовании
— точка, в которую при преобразовании 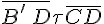 и, значит, точки
и, значит, точки 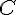 совпадают, т.е. точка
совпадают, т.е. точка  и
и 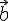 называется вектор
называется вектор 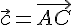 , где
, где 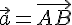 ,
, 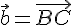 ,
, 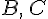 — точки, полученные после откладывания векторов
— точки, полученные после откладывания векторов 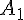 --- любая точка, отличная от точки
--- любая точка, отличная от точки 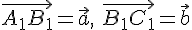 . Докажем, что
. Докажем, что 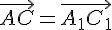 .
.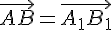 и
и 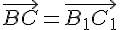 , то по лемме2.1.
, то по лемме2.1. 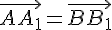 и
и  , то есть
, то есть 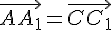 . Следовательно, по той же лемме
. Следовательно, по той же лемме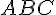 . Поэтому правило сложения векторов называется правилом треугольника. Из этого правила следует, что для любых трех точек
. Поэтому правило сложения векторов называется правилом треугольника. Из этого правила следует, что для любых трех точек 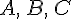 справедливо равенство
справедливо равенство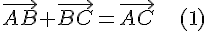
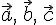 справедливы следующие равенства:
справедливы следующие равенства: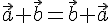 --- коммутативность сложения векторов.
--- коммутативность сложения векторов.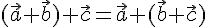 --- ассоциативность сложения векторов.
--- ассоциативность сложения векторов.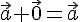 .
.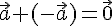 .
.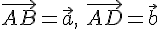 , а затем от точки
, а затем от точки 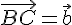 . Согласно построению
. Согласно построению 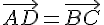 , поэтому по лемме 2.1. получаем
, поэтому по лемме 2.1. получаем 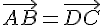 , т.е.
, т.е. 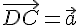 .
.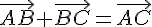 и
и 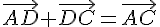 , следовательно,
, следовательно, 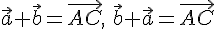 . Отсюда получаем, что
. Отсюда получаем, что 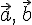 и
и  --- произвольные векторы. Возьмем какую-нибудь точку
--- произвольные векторы. Возьмем какую-нибудь точку 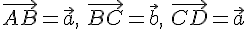 .
. 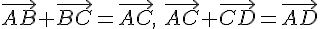 , поэтому
, поэтому 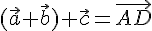 . С другой стороны
. С другой стороны  , поэтому
, поэтому 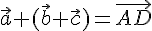 . Отсюда получаем требуемое.
. Отсюда получаем требуемое.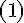 к точкам
к точкам 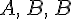 получим
получим .
.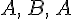 получим
получим 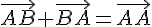 .
.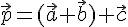 . На основании доказанной теоремы
. На основании доказанной теоремы 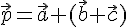 , поэтому при записи суммы трех векторов можно опустить скобки и писать просто
, поэтому при записи суммы трех векторов можно опустить скобки и писать просто  . Более того, можно доказать, что сумма трех векторов не зависит от порядка слагаемых. В самом деле, докажем, например, что
. Более того, можно доказать, что сумма трех векторов не зависит от порядка слагаемых. В самом деле, докажем, например, что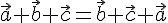 :
: .
.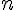 векторов, где
векторов, где 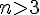 . Пусть
. Пусть 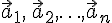 --- произвольные векторы. Их суммой называется вектор
--- произвольные векторы. Их суммой называется вектор 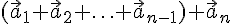 , и обозначается так:
, и обозначается так: 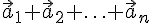 .
. 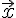 , который в сумме со вторым вектором дает первый вектор.
, который в сумме со вторым вектором дает первый вектор.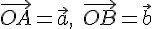
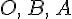 получаем
получаем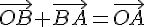
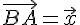 , будем иметь
, будем иметь 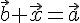 . Этим доказано существование разности.
. Этим доказано существование разности. такой, что
такой, что 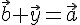 . Тогда
. Тогда 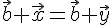 . Прибавим к обеим частям этого равенства вектор
. Прибавим к обеим частям этого равенства вектор 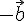 . Получим
. Получим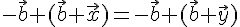
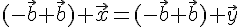
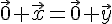
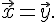
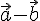 .
.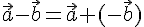

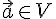 на действительное число
на действительное число 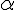 называется вектор
называется вектор 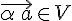 , который удовлетворяет двум условиям:
, который удовлетворяет двум условиям: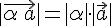 ;
;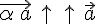 , если
, если 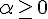 и
и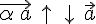 , если
, если  .
.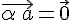 тогда и только тогда, когда
тогда и только тогда, когда 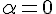 или
или  .
.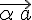 будем употреблять запись
будем употреблять запись 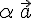
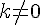 называется такое преобразование плоскости, при котором каждой точке
называется такое преобразование плоскости, при котором каждой точке 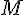 ставится в соответствие точка
ставится в соответствие точка 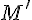 такая, что выполнены следующие условия:
такая, что выполнены следующие условия: лежат на одной прямой;
лежат на одной прямой;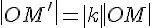 ;
;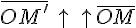 , если
, если 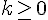 и
и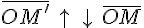 , если
, если 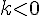 .
.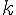 треугольник
треугольник 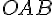 переходит
переходит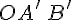 , то
, то  .
.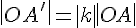 и
и 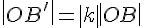 , поэтому
, поэтому  подобен
подобен 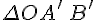 с коэффициентом
с коэффициентом 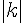 . Отсюда следует, что
. Отсюда следует, что 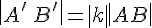 и
и 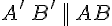 . Если
. Если 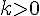 , то точки
, то точки 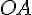 , поэтому
, поэтому 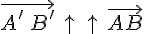 , следовательно,
, следовательно, 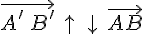 , т.е. и в этом случае
, т.е. и в этом случае 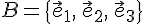 --- базис пространства
--- базис пространства 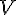 и пусть в этом базисе векторы
и пусть в этом базисе векторы 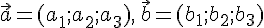 . Тогда для любых действительных чисел
. Тогда для любых действительных чисел 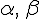 вектор
вектор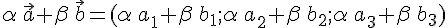
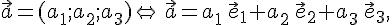
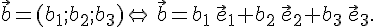
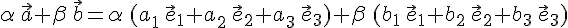


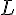 --- непустое множество векторов из векторного пространства
--- непустое множество векторов из векторного пространства 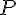 . Множество
. Множество 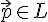 и
и  , то
, то  .
.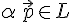 для любого вещественного числа
для любого вещественного числа 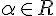 .
.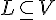 , а в
, а в 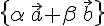 ,
,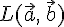 . Пусть
. Пусть 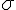 --- плоскость, которой параллельны векторы
--- плоскость, которой параллельны векторы 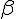 векторы
векторы 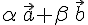 линейно зависимы, поэтому они компланарны, то есть вектор
линейно зависимы, поэтому они компланарны, то есть вектор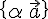 ,
,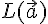 . Пусть
. Пусть 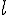 --- прямая, которой параллелен вектор
--- прямая, которой параллелен вектор 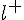 --- ось и
--- ось и 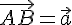 --- некоторый вектор. Обозначим через
--- некоторый вектор. Обозначим через 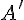 и
и 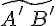 направленного отрезка
направленного отрезка 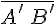 на оси.
на оси.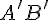 , взятое с определенным знаком.
, взятое с определенным знаком.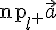 . В случае ортогонального проектирования применяется обозначение
. В случае ортогонального проектирования применяется обозначение 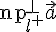 . Отметим, что
. Отметим, что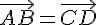 . Обозначим через:
. Обозначим через: проекции точек
проекции точек 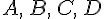 . Так как
. Так как  совпадает с серединой отрезка
совпадает с серединой отрезка  , значит,
, значит, 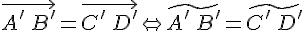 .
.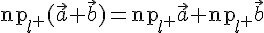
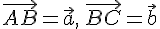 тогда
тогда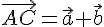 . Обозначим через:
. Обозначим через: 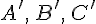 проекции точек
проекции точек 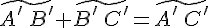 .
.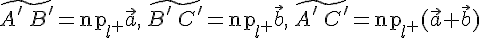 .
.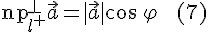
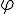 --- угол между вектором
--- угол между вектором 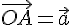 . Так как проекции равных векторов равны между собой, то можно считать, что вектор
. Так как проекции равных векторов равны между собой, то можно считать, что вектор 
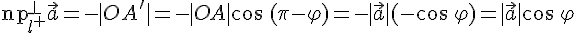
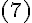 очевидна.
очевидна.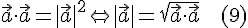
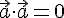 тогда и только тогда, когда вектор
тогда и только тогда, когда вектор 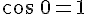 .
. или
или 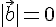 или
или 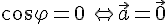 или
или 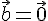 или
или 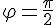 .
.


