
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные виды параллельного проектирования
В геометрии рассматриваются следующие три вида параллельного проектирования. 1. Проекция точек плоскости на прямую Пусть на плоскости заданы две пересекающиеся в точке Итак: Ортогональной проекцией
Пусть в пространстве задана плоскость Итак: ортогональной проекцией
3. Проекция точек пространства на прямую Пусть в пространстве задана плоскость Отметим в заключение, что ортогональное проектирование точки
ортогональной проекцией точки Нетрудно убедиться в том, что при любом из рассмотренных видов параллельного проектирования отрезок проектируется в отрезок, причем, середина отрезка проектируется в середину. Проекция вектора на ось Пусть Замечание 14.1. Согласно определению 11.1. проекция вектора на ось --- это число, равное длине отрезка Проекцию вектора Кроме того отметим, что проекцию вектора мы определили через проекцию его представителя, поэтому необходимо доказать, что это определение не зависит от выбора представителя. Это доказательство отнесем к свойствам Свойства проекций векторов на ось. 2. Проекция суммы векторов на ось есть сумма проекций слагаемых векторов, т.е.
Доказательство. Пусть
Для завершения доказательства достаточно заметить, что 3. Для ортогональной проекции
где Доказательство. Пусть
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.227.69 (0.01 с.) |
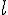 параллельно прямой
параллельно прямой 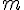 .
.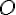 прямые
прямые 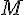 плоскости не лежит на прямой
плоскости не лежит на прямой 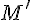 пересечения прямой
пересечения прямой  параллельно прямой
параллельно прямой 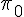 .
.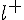 --- ось и
--- ось и 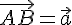 --- некоторый вектор. Обозначим через
--- некоторый вектор. Обозначим через 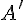 и
и 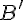 параллельные проекции точек
параллельные проекции точек 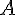 и
и 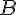 на прямую
на прямую 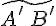 направленного отрезка
направленного отрезка 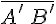 на оси.
на оси.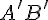 , взятое с определенным знаком.
, взятое с определенным знаком.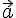 на ось
на ось 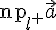 . В случае ортогонального проектирования применяется обозначение
. В случае ортогонального проектирования применяется обозначение 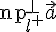 . Отметим, что
. Отметим, что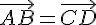 . Обозначим через:
. Обозначим через: проекции точек
проекции точек 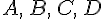 . Так как
. Так как 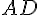 и
и 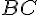 совпадают и, кроме того, при параллельном проектировании середина отрезка проектируется в
совпадают и, кроме того, при параллельном проектировании середина отрезка проектируется в совпадает с серединой отрезка
совпадает с серединой отрезка  , значит,
, значит, 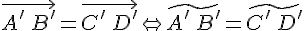 .
.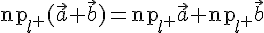
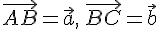 тогда
тогда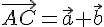 . Обозначим через:
. Обозначим через: 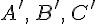 проекции точек
проекции точек 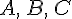 . Используя основное тождество (см. теорему 12.1.) для точек
. Используя основное тождество (см. теорему 12.1.) для точек 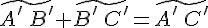 .
.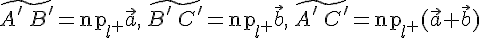 .
.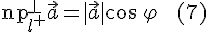
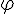 --- угол между вектором
--- угол между вектором 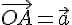 . Так как проекции равных векторов равны между собой, то можно считать, что вектор
. Так как проекции равных векторов равны между собой, то можно считать, что вектор 
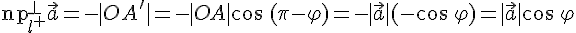
 или он перпендикулярен оси, формула
или он перпендикулярен оси, формула 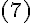 очевидна.
очевидна.


