Практическая работа по теме «задачи на разрезание»

Задача 1. Можно ли квадрат 5 на 5 разрезать на прямоугольники 1 на 2?

Ответ: нет

Задача 2. Вася купил шоколадку 5 на 5, разделенную по бороздкам на 25 маленьких квадратиков. Удастся ли ему разломать эту шоколадку на уголки из трех квадратиков?

Ответ: нет

Задача 3. Можно ли прямоугольник 6 на 9 разрезать на уголки из трех клеток?

Ответ: да

Задача 4. Покажите, как разрезать квадрат размером 5×5 клеток на "уголки" шириной в одну клетку так, чтобы все "уголки" состояли из разного количества клеток. (Длины "сторон" уголка могут быть как одинаковыми, так и различными).

Решение: площадь квадрата – 25 клеток, а самого маленького "уголка" – 3 клетки. Представим число 25 в виде суммы различных слагаемых, начиная с трёх: 25 = 3 + 4 + 5 + 6 + 7, и разрежем квадрат на пять "уголков" с таким количеством клеток. Например:

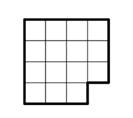
Задача 5. Разрезать фигуру на две равные части, из которых можно было бы сложить квадрат.

Решение:

Задача 6. Разрезать фигуру на четыре равные части.

Решение:

Задача 7. Разрезать фигуру на четыре равные части.

 

Решение:

Задача 8. Разрезать фигуру на четыре равные части.

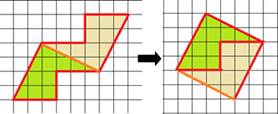
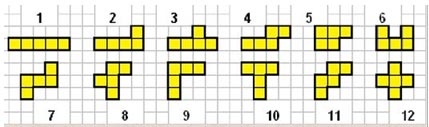
Решение:

Задача 9. Перед вами два квадрата, один из которых уже разделен на четыре одинаковых треугольника. Как при помощи этих треугольников и маленького квадрата сложить один большой квадрат? Ничего больше разрезать не требуется.

Решение:

Задача 10. Сложите из двенадцати фигур Пентамино прямоугольник 6 × 10, причем так, чтобы каждый элемент касался какой-нибудь стороны этого прямоугольника.

Вообще данная задача напоминает нам детскую игру тетрис. Увлекательно и полезно для детей начиная с 5-летнего возраста, что развивает логику и мышление.

Детали для игры – задачи должны быть подготовлены заранее. Удобнее всего это делать на клетчатой бумаге.

Заметим, что каждая часть содержит в себе пять одинаковых квадратиков. А теперь применяя логическое мышление, решаем задачу. Строить прямоугольник начнем с прямого угла.

Решение:

Самостоятельная работа «Принцип Дирихле»

Задача 1. В мешке лежат шарики двух разных цветов: черного и белого. Какое наименьшее количество шариков нужно вынуть из мешка, чтобы среди них точно два шарика оказались одного цвета?

Задача 2. Вдоль круглого стола равномерно размещены таблички с фамилиями дипломатов, участвующих в переговорах. После начала переговоров оказалось, что каждый из дипломатов не сидит напротив своей таблички. Можно вернуть стол так, чтобы, по крайней мере, два дипломата сидели напротив своих табличек?

Задача 3. В городе более 8000 тысяч жителей. Ученые считают, что у каждого человека менее 200000 волос на голове. Докажите, что существует, по крайней мере, 41 житель с одинаковым количеством волос на голове.

Задача 4. На пяти полочкам книжного шкафа 161 книга, причем на одной из полок - 3 книги. Докажите, что найдется полочка, на которой не менее 40 книг.