
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритми розв'язання позиційних задачСодержание книги
Поиск на нашем сайте
Перетин кривих поперхонь площиною. Якщо поверхня задана у прямокутних декартових координатах явною чи неявною формою, а січна площина — будь-яким визначником, то взявши координати трьох неколінійних точок, що належать січній площині, обчислимо коефіцієнти А, В, С, D за формулами (1.85) і дістанемо рівняння січної площини в неявній формі (1.83). Визначимо тип системи, в якій січна площина є площиною рівня, а також обчислимо параметр відповідної системи спеціальних координат. У результаті матимемо рівняння січної площини в параметричній формі. Підставивши здобуті вирази у рівняння поверхні зведемо його до рівняння з двома змінними u та v. Якщо це рівняння можна розв'язати відносно однієї із змінних, тобто знати функцію v = v(u), то, надаючи u значення і деяким кроком маємо відповідні значення. Оскільки uOv є прямокутною декартовою системою на січній площині, то лінія перетину, віднесена до цієї системи, визначається в натуральному вигляді. Що6 скласти її рівняння у просторі, треба підставити відповідні значення u та v в параметричні рівняння січної площини. Приклад. Нехай треба знайти рівняння лінії перетину центральної поверхні обертання другого порядку (1.93) і площини, заданої трьома точками M0(x0, y0, z0), M1 (x1, y0, z1), M2 (x2, y2, z2). Застосування формулу (1.85) дістанемо: А¹0, В¹0, С¹0, D¹0), знаходимо
Підставивши ці вирази дістанемо параметричні рівняння січної площини:
Тепер підставимо вирази (1.125) у рівняння поверхні (1.93). У результаті матимемо
Це рівняння другого ступеня відносно Натуральний вигляд лінії перетину знайдемо побудовою графіка функції (1.126) за її рівнянням у системі uОv. Масиви координат uі, vі, що визначаються в процесі побудови, підставимо в параметричні рівняння січної площини (1.125). Дістанемо просторові координати хі уі zі, точок, які визначають лінію перетину. Наведемо приклади програмної реалізації цього алгоритму для двох поверхонь, що перетинаються площиною. На рис. 23.1 наведено в ізометричній проекції поверхню еліпсоїда обертання за функцією (1,93) при а = 3, с = 5, р = 1, q = 1, що перетинаються площиною [див. рівняння (1.85)] при А = 1, В = 3, С = 16, D = -16.
На рис. 23.2 зображено в ізометричній проекції поверхню однопорожнинного гіперболоїда, що перетинається тією самою січною площиною. Порівняно з попередніми вхідні дані відрізняються тільки значенням р, яке в цьому випадку набуває значення -1. Застосуємо наведений алгоритм для побудови лінії перетину прямої призми та
площини. Нехай січна площина має такі коефіцієнти A, B, C, D при яких виконуються рівності (1.124) і (1.125). Позначимо
Це є рівнянням лінії перетину і рані призми із січною площиною у системі uОv на січні із площині. Підставляючи замість u його значення з рівняння (1.120), знайдемо координати uі та vі, точок перетину ребер призми із січною площиною. Нагадаємо, що замість t треба підставляти у рівняння (1.126а) послідовно значення з формули (1.119). Масиви просторових координати xі, yі, zі , вершин шуканої лінії перетину знайдемо підстановкою uі та vі, у рівняння (1.125). Приклади програмної реалізації наведеного алгоритму показано на рис.1.14-1.16. В ізометричній проекції подано правильну дванадцятигранну призму, висота якої 12 см, радіус описаного циліндра 5см, а кутовий параметр однієї з вершин нижньої основи становить 0,13 рад. ІІризму перетинає прощина
Використовуючи замість (1.85) рівняння сім’ї площин (1,86), матимемо алгоритм побудови лінії перетину правильної піраміди та площини. На рис.1.117 подано ізометричну проекцію правильної дванадцятигранної піраміди, висота якої 12 см, кут між бічною гранню і висотою 0,35 рад, а кутовий параметр основи вершин основи становить 0.26 рад. Піраміду перетинає площина
В алгоритмі розв'язання позиційних задач на перетин прямої чи кривої лінії поверхнею, площини з поверхнею та взаємний перетин двох поверхонь передбачається розв'язання системи рівнянь заданих геометричних образів. Алгоритм грунтується на ідеї належності точки до внутрішності чи зовнішності поверхні. Якщо лінія та поверхня задні в одній системі координат, то завжди можна застосувати один з двох алгоритмів (площинний чи просторовий) визначення належності будь-якої точки внутрішності чи зовнішності поверхні.
Площинний алгоритм. Позначимо функціональний параметр рівняння лінії через s. Нехай розв'язок лежить в інтервалі s1<s<s2. Визначимо координати x, y, z точки М, що відповідає значенню
Обчислимо значення спеціальних координат u, v, t у системі, до якої віднесено поверхню. Підставляючи значення t у внутрішнє рівняння поверхні, дістанемо ріння лінії рівня t=const цієї поверхні. Скориставшись формулами та враховуючи, що роль x і у відіграють u і v відповідно, визначимо належність точки М до внутрішності чи зовнішності лінії рівня t = соnst заданої поверхні. Якщо точка М належить до зовнішності лінії рівня, то функціональний параметр наступної довільної точки М визначаємо за формулою (1.127). надаючи s1 значення sM. Якщо точка M належить до внутрішності, то значення sM надаємо s2. Ітераційний процес продовжуємо доти, доки виконується умова Значення функціонального параметра довільної точки, при якому виконується ця умова, треба підставити в рівняння лінії, щоб дістати просторові координаті x, y, z шуканої точки перетину.
Просторовий алгоритм. Для поверхонь другого порядку (1.119). (1.122) при розгляді питання про належність довільної точки до внутрішності чи зовнішності поверхні не обов'язково переходити до рівняння лінії ріння цієї поверхні. Досить підставити координати x, y, z довільної точки в рівняння (1.119) або (1.122). Якщо знак "=" - змінюється на знак “>”, то довільна точка належить до зовнішності, якщо на знак " < ", то до внутрішності поверхні. Просторовий алгоритм більше нічим не відрізняється від площинного. Якщо поверхня перетинається площиною чи іншою поверхнею, то до алгоритму додасться визначення на площині чи на поверхні сім'ї ліній рівня. Розв'язок шукають для кожної лінії, а масиви координат точок перетину впорядковують згідно із зростанням чи спаданням значення параметра сім'ї.Візуалізація ліній та поверхонь Геометричну модель відображення лінії чи поверхні засобами комп'ютерної графіки дістають методом проекцювання та сполучення точок, які лежать на лінії, впорядкованих відповідно із зростанням або спаданням значення функціонального параметра. Вхідні дані у вигляді рівняння лінії та інтервалу значень функціонального параметра дають змогу обчислити координати x, y, z послідовності точок. Щодо візуалізації поверхні, то проекції відтворюють деякі характерні для поверхні лінії: ребра багатогранників, лінії, обвідну проекції кривої поверхні, межі відсіку поверхні. Ефективний спосіб візуалізації кривої поверхні полягає в попередньому визначенні на поверхні сім'ї або сітки координатних ліній та відображенні на проекції видимих відрізків (рис.1.17 …рис.1.22) та відповідно для прямокутних ізометрії, диметрії та косокутної диметрії. Точкове відображення простору на фронтальну площину проекцій визначено формулами
а на горизонтальну площину проекцій — формулами
Визначення лінії, обвідної проекції поверхні. Нехай поверхня задана в параметричній формі:
Як було показано, явна форма задання поверхні є окремим випадком задання у формі (1.130). До форми (1.130) приводить також задання поверхні внутрішнім рівнянням у спеціальних координатах. Застосовуючи формули відповідного точкового перетворення простору при проекціюванні, можна записати
де х, у -- прямокутні декартові координати проекцій точок; f,j — функції, що реалізують ланцюжок —одну з функцій -- (1.128), (1.129). Проаналізувавши вирази (1.131), дійдемо висновку, що ці рівняння відповідають рінянням двох сімей ліній u=const, t=const Кожна сім'я залежить від одного параметра. Як відомо, такі сім'ї мають обвідну, рівняння якої
Обвідна (1.132) поділяє точки на поверхні (1.130) на два класи, що визначаються знаком нерівності, в яку перетворюється ліва частина (1.132) після підстановки внутрішніх координат u, t довільної точки на поверхні. Отже, в результаті підстановки внутрішніх координат u, t точки на поверхні ліву частину (1.132) дістанемо один з трьох випадків: І=0, (1.133) коли точка належить обвідній. За цієї умови можна скласти рівняння обвідної і побудувати її: І>0, (1.134) коли точка є видимою на проекції; І<0, (1.135) коли точка невидима на проекції. Випадок (1.134) або (1.135) завжди можна дістати множенням лівої частини (1.132) на -1. Підкреслимо, що тут ідеться про потенціальну видимість, тобто не враховується випадок, коли інша поверхня закринає собою розглядувану поверхню при проекціюванні. У табл. 1.1 наведено приклади застосування форм задання та алгоритму визначення видимості найпоширеніших поверхонь. Для більшої наочності на поверхнях відтворено сітку координатних ліній, завдяки застосуванню алгоритму визначення видимості на проекціях відтворена зовнішність поверхні, а для таких поверхонь, як параболоїд, катеноїд, псевдосфера відтворена також їхня внутрішність, яку видно крізь отвір. В цьому разі контур отвору с нерухомим екраном, що обмежує видиму внутрішність поверхні.
Табл.1.2 Поверхні в ортогональних проекціях та в ізометрії ізометрії
Щодо побудови проекції обвидної, то в багатьох випадках це можна зробити, розв'язуючи рівняння (1.123) відносно однієї з дих змінних. Так для циліндра та конуса (див. табл. 1.1) обидва розв'язки не залежать від другої змінної, для центральних поверхонь другого порядку рівняння (1.123) є квадратним відносно лінійної змінної. Розв'язки цього рівняння використано також для каналової поверхні, різьбленої поверхні Монжа, катеноїда, псевдосфери. Для гранних поверхонь алгоритм визначення видимості полягає в порівнянні знаків лівої частини (1.123) для суміжних граней. Якщо Іі>0, Іі+1 > 0, (1.136) то ребро, по якому перегинаються ці грані, видиме; якщо Іі Іі+1 < 0, (1.137) то ребро контурне; якщо Іі<0, Іі+1 < 0, (1.138) то ребро невидиме. Моделювання розгорток До розгортних належать такі поверхні: багатогранники, циліндри, конуси та торси. Задача розгортування полягає в знаходженні функцій
або з урахуванням залежності прямокутних декартових координат точки на циліндрі чи конусі від відповідних спеціальних координат, в яких ці поверхні мають рівняння u=0,
У формулах (1.139) та (1.140) xp, yp -- декартові прямокутні координати на площині розгортки, x, y, z — декартові прямокутні координати точки, що належать розгортній поверхні. Циліндр. Для циліндра, радіус основи якого r формули (1.140) мають вигляд
Правильна призма. Нехай правильна n-гранна призма описана навколо циліндра радіуса r і має висоту h. Кутовий параметр однієї з вершин відносно площини визначимо через tH. Апофеми бічних граней призми мають узагальнену циліндрічну координату
Знайдемо
дістанемо таке значення j = 1, при якому ця умова виконується. Позначимо
Тоді координата u точки на поверхні призми в узагальненій ціліндричній системі виражається рівністю
 
Формули (1.141) мають вигляд
де v = z. Нагадаємо, що координати точки x, y, z на поверхні призми вважаємо заданими. Конус. У гіперболічних координатах рівнянням конуса є u = 0. Формули (1.140) набувають вигляду
де a — кут між віссю та твірною конуса. Правильна піраміда. Правильну піраміду віднесемо до вписаного в неї конуса. Кут a між його твірною та віссю входить до визначника піраміди. Як і для призми, tH — кутовий параметр однієї з вершин основи піраміди відносно площини х0z. Обчислимо ti за формулою (1.142), та р — за формулою (1.144), b та j — за формулою (1.143). Потім знаходимо:
Функції (1.140) мають вигляд
Па рис.1.23,1.28, наведено приклади програмної реалізації алгоритму визначення лінії взаємного перетину поверхонь та алгоритмів моделювання розгорток, На рис. 1.23 зображено конус і циліндр, які перетинаються. На рис.1.24 і рис. 1.26 подано розгортки конуса й циліндра відповідно з визначенням на розгортці лінії взаємного перетину. На рис. 1.27 показано два циліндри, які перетинаються, а на рис. 1.25 і рис. 1.28 — розгортки поверхонь циліндра з горизонтальною та вертикальною осями відповідно з визначенням на розгортці лінії перетину.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.205.123 (0.012 с.) |

 (1.124)
(1.124) (1.125)
(1.125) (1.126)
(1.126) u та v, тобто його можна розв'язати відносно будь-якої з цих змінних.
u та v, тобто його можна розв'язати відносно будь-якої з цих змінних. і підставимо вирази (1.124) у рівняння (1.85), що при значеннях t згідно з рівнянням (1.119) є рівнянням граней призми, В результаті матимемо
і підставимо вирази (1.124) у рівняння (1.85), що при значеннях t згідно з рівнянням (1.119) є рівнянням граней призми, В результаті матимемо . (1.126а)
. (1.126а)
 .
. . (1.127)
. (1.127) , де e визначає наперед задану точність.
, де e визначає наперед задану точність. , (1.128)
, (1.128) . (1.129)
. (1.129) (1.130)
(1.130) . (1.131)
. (1.131) . (1.132)
. (1.132) 







 , (1.139)
, (1.139) (1.140)
(1.140) (1,141)
(1,141) . (1.142)
. (1.142) а з умови
а з умови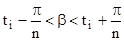 (1.143)
(1.143) (1.144)
(1.144) (1.145)
(1.145)





 , (1.146)
, (1.146) (1.147)
(1.147)
 . (1.148)
. (1.148)


