
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометричне моделювання на площиніСтр 1 из 10Следующая ⇒
Вступ На початку свого розвитку комп'ютерну графіку розглядали, як частину системного програмування для ЕОМ чи один з розділів систем автоматизованого проектування (САПР). Сучасна комп'ютерна графіка складає ряд напрямків і різноманітних застосувань. Для одних з них основою є автоматизація креслення технічної документації, для інших - проблеми оперативної взаємодії людини і комп'ютера, а також задачі числової обробки, розшифровки і передачі зображень. Сучасне розширення можливостей ЕОМ, створених для виконання обчислень, дає можливість комп'ютеру сприймати і наочно зображувати результати розрахунків, будувати необхідні комплексні креслення, схеми і т.п.. Зорове сприйняття графічної інформації для людини має важливе значення, обсяг і швидкість сприйняття зорових образів значні. Для представлення особливостей чи креслення будь-якого процесу досить декількох секунд, під час яких ми розглядаємо креслення, графік чи функції інше наочне зображення. Отже, важливість наочного представлення комп'ютером результатів числення важко переоцінити. Однією з основних підсистем САПР, что забезпечує комплексне виконання проектних робіт на основі ЕОМ, є комп'ютерна графіка (КГ). Комп'ютерною чи машинною графікою називають наукову дисципліну, що розробляє сукупність засобів і прийомів автоматизації кодування, обробки і декодування графічної інформації. Іншими словами, комп'ютерна графіка розробляє сукупність технічних, програмних, інформаційних способів і методів зв'язку користувача з ЕОМ на рівні зорових образів для рішення різноманітних задач при виконанні конструкторської і технічної підготовки виробництва. Ведеться інтенсивний пошук шляхів і способів рішення проблеми різкого підвищення продуктивності інженерної роботи під час виконання креслярсько-графічних робіт, конструкторської і технологічної підготовок виробництва. Це викликано потребою ліквідувати розрив, що утворився між відносно високою продуктивністю автоматизованого процесу основного виробництва і низкою продуктивністю ручного чи механізованого процесу конструкторської і технічної підготовки виробництва. Вивчення комп'ютерної графіки обумовлено: · широким упровадженням системи комп'ютерної графіки для забезпечення систем автоматизованого проектування, автоматизованих систем конструювання (АСК) і автоматизованих систем технометричної інформації, що складає 60...80 % загального обсягу інформації, необхідної для проектування, конструювання і виробництва літаків, кораблів, автомобілів, складних архітектурних споруджень і т.п.:
· необхідністю автоматизації виконання численних креслярсько-графічних робіт; · необхідністю підвищення продуктивності і якості інженерної роботи.
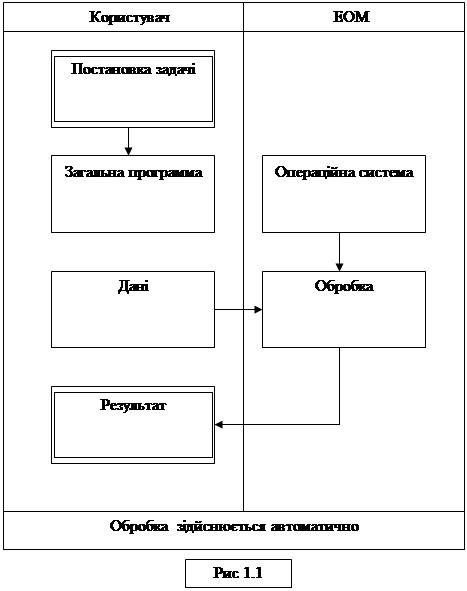
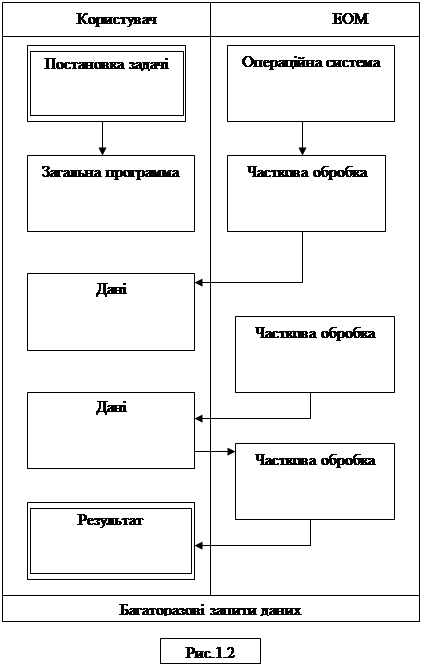
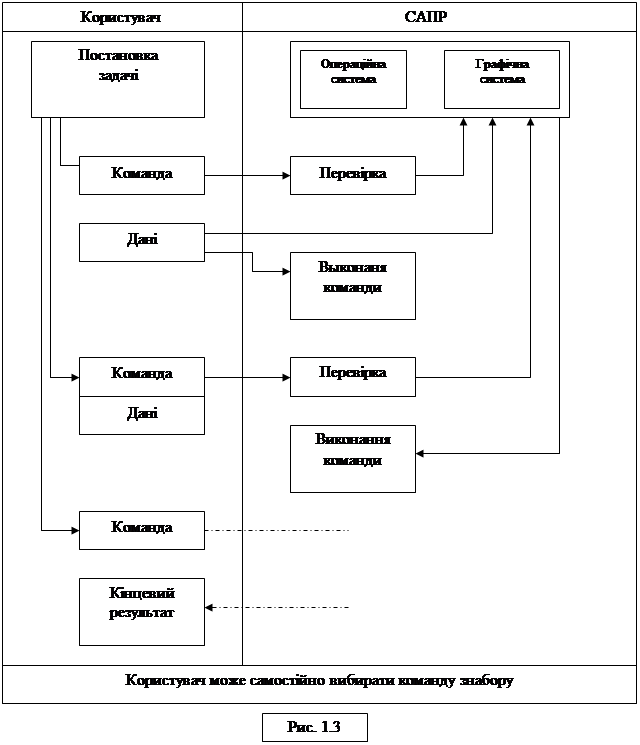
Метою комп'ютерної графіки є підвищення продуктивності інженерної роботи і якість проектів, зниження вартості проектних робіт, скорочення термінів виконання їх. Задачею комп'ютерної графіки є звільнення людини від виконання трудомістких графічних операцій, які можна формалізувати: пошук оптимальних рішень, забезпечення природного зв'язку людини з ЕОМ на рівні графічних зображень. Розвиток комп'ютерної графіки (КГ) почався з появою пристроїв графічного ведення. Становлення КГ і широке її використання зв'язане зі створенням засобів графічного введення — виводу і дисплеїв — пристроїв побудови зображень на електронно-променевій трубці. При взаємодії користувача з комп'ютером розрізняють три режими роботи: пакетний; пасивно-интерактивный; інтерактивний. У пакетному режимі роботи графічна інформація формується і виводиться за допомогою заздалегідь написаного пакета прикладних програм — ППП (рис 1.1). Формування і висновок простих зображень у пакетному режимі на пристроях одержання твердих копий (телетайп, АЧПП) здійснювалося ще до початку використання комп'ютерів. У пасивно-інтерактивному режимі роботи графічна інформація формується і виводиться за допомогою заздалегідь написаних прикладних програм, у яких в яких передбачено багаторазові запити даних у користувача (Рис. 1.2). В інтерактивному режимі роботи графічна інформація формується і виводиться в режимі оперативно графічної взаємодії користувача і комп'ютера (Рис.1.3). Початком сучасної інтерактивної комп'ютерної графіки можна вважати дисертацию Сазерленда (1963 р.), присвячену графічній системі SKETCHPAD. Ця система могла відтворювати і перетворювати геометричні фігури за допомогою світлового пера. Робоче поле екрана поділяється на чотири частини для побудови проекцій об'єкта: вид перед, ліворуч, зверху й у перспективі. Будь-яка зміна однієї з проекцій автоматично визначала зміну всіх інших проекцій і зображення в перспективі. Отже, зрозуміло, наскільки широкі можливості комп'ютерної графіки
для автоматизації креслярсько-графічних робіт з великим обсягом графічного матеріалу при машинному проектуванні й автоматизації виробництва в багатьох областях промисловості. У 60-роках виникає ряд дослідницьких проектів, з'являються розробки, придатні для комерційного поширення. Найбільш значними серед них були проекти фірми GENERAL MOTORS з використанням графічної системи з розподілом часу для багатьох етапів проектування автомобілів, система Digidraphic була створена фірмою для проектування лінз і дисплейна система ІВМ 2250, заснована на прототипі фірми GENERAL MOTORS.
В Україні перша інтерактивна графічна система автоматизованого проектування електронних схем була розроблена Київським політехнічним інститутом і Науково-дослідним інститутом автоматизованих систем керування і плануванні в будівництві (НДІАСК, Київ) і демонструвалася в 1969р. Застосування КГ для формування різноманітної графічної інформації в різних областях людської діяльності свідчить про те, що комп'ютерна графіка і геометрія явища різноманітні і багатопланові. У рамках КГ зважуються такі проблеми: · розробка нових методів математичного забезпечення; · розробка програмних систем графічних мов; · створення нових ефективних технічних засобів для проектувальників, конструкторів і дослідників; · розвиток нових наукових дисциплін і навчальних предметів, що увібрало в себе аналітичну, прикладну і нарисну геометрію; · програмування для ЕОМ, методи обчислювальної математики, приладобудування. Комп'ютерна графіка складає цілий ряд напрямків і має різне застосування. За допомогою КГ вирішують багато графічних задач. У комп'ютері синтезуються прості і складні об'єкти: поверхні, тіла, структури. Без швидкого і точного рішення графічних і геометричних задач не можна освоювати космос, конструювати складні механізми і машини, будувати інженерні спорудження, розвивати медицину і т.п.. Комп'ютерну графіку широко застосовують при рішенні актуальної проблеми підвищення продуктивності і точності інженерної роботи. Цього досягають автоматизацією розрахунково-графічних робіт, вирішуючи різноманітні задачі в області машинобудування, літакобудування, профілювання складного різального інструмента і т.п.. Комп'ютерну графіку широко застосовують також при рішенні актуальної проблеми підвищення продуктивності і якості виготовлення виробів основного виробництва. Цьому сприяє автоматизована система технологічної підготовки виробництва {АСТПВ}, під якою розуміють будь-який автоматизований виробничий процес, яким керує комп'ютер. Найважливішими автоматизованими виробничими комплексами АСТПВ є: верстати з числовим програмним керуванням (ЧПК), верстат з мини-еом, програмно-керовані роботи, гнучкі виробничі системи. Усі види інженерної діяльності, керовані комп'ютерами, об'єднані за назвою автоматизованої системи інженерного забезпечення (АСІЗ), що включає:
· планування процесу проектування з використанням комп'ютерного програмного забезпечення; · системи автоматизованого проектування різального інструмента і процесу обробки: · процедури автоматизованої системи керування виробництвом (АСУП); · процедури автоматизованої системи виробничого планування (АСВП) · системи автоматизації проектування, розміщення, оснащення на виробництві, зокрема графічну імітацію робототехніки. Цілковиту інтеграцію областей АСІЗ разом з економічними і бухгалтерськими системами називають комп’ютерно інтегрованим виробництвом (КІВ). КІВ ще тільки починає розвиватися на основі комп'ютерної графіки і, як правило, функціонує під керуванням головних комп'ютерів із загальною базою даних.
Пряма Різноманітність форм задання прямої, взагалі будь-якого геометричного образу, зумовлена зручністю застосування тієї чи іншої форми при розв'язанні конкретних задач. Тому перелік форм задання буде супроводжуватися даними про галузі застосування. Пряма в явній формі
де k — тангенс кута нахилу прямої до осі абсцис; b — початкова ордината. Рівняння (1.2) називають рівнянням з кутовим коефіцієнтом. Ця форма дуже зручна для виразу умов паралельності (k1=k2) та перпендикулярності ( В алгоритмі покриття замкненої області штриховкою рівнянням (1.2) задають сім'ю паралельних ліній штриховки, змінюючи b з фіксованим кроком. В алгоритмі обчислення площі замкненої області підінтегральна функція є правою частиною рівняння (1.2). Форму (1.2) застосовують також в алгоритмі перетворення симетрії відносно прямої загального положення. Пряма в неявній формі Ах + Ву + С = 0 (1.2) Ліву частину цього рівняння застосовують для задання півплощин Ах + Ву + С > 0 (1.3) Ах + Ву + С < 0, (1.4) Якщо прийняти, яка з цих півплощин розміщена зліва, а яка справа від прямої, то цим самим можна орієнтувати пряму (1.2). Для зміни напряму прямої (1.2) на протилежний треба обидві частини рівняння (1.2) помножити на -1. При цьому півплощини (1.3) і (1.4) поміняються місцями.
Сукупністю нерівностей, кожна з яких задає півплощину, задають область, обмежену опуклим багатокутником на площині, якщо кількість нерівностей менша від трьох. При цьому можна використовувати нерівності лише одного знака. Наприклад, внутрішність квадрата, зображеного на рис. 1.4 моделюється системою нерівностей -у + 2 > 0, -х + 2 > 0, у + 2 > 0, х + 2 > О, (1.5) а зовнішність квадрата, зображеного на рис. 1.5, — системою нерівностей. у - 1 > 0, х - 1 > 0, -у - 1 > 0, -х - 1 > О, (1.6) "Кільцева" область (рис. 1.6), яка обмежена двома попередніми квадратами моделюється системою з восьми нерівностей (1.5) і (1.6). Обчислення координат точки перетину двох прямих. Якщо прямі задані формою (1.2)
А1х+В1у+С1 =0, (1.7) А2х+ В2у+ С2=0, то координати точки перетину їх обчислюють за формулами
Якщо D = 0, а Dx ¹О або D y¹0, то прямі паралельні. Якщо D=0, Dx= О, Dy= 0, то прямі збігаються. Рівняння прямої, що проходить через дві точки, має вигляд Це рівняння доцільно застосовувати тоді, коли впорядкована послідовність точок сполучається ламаною. Ця послідовність задається масивами координат хi, уi (і =1,2,..., n). Рівняння ланок ламаної дістанемо у вигляді
Рівняння (1.9) можна звести до вигляду (1.1), якщо обчислити k і b за формулами
та до вигляду (1.2), якщо обчислити А, В і С за формулами
Розглянемо ще параметричну форму за-дання прямої. Запишемо рівняння (1.9) у вигляді
Звідси
де s є параметром. Якщо s = 0, то x = x1|, у = y1. Якщо s = 1, то x2 = х, у = у2. Якщо О <д< 1, то точка лежить усередині відрізка (x1, y1), (y2, x2). Якщо s<0 або s >1, то точка лежить зовні відрізка. Параметричне рівняння (1.14) застосовують у багатьох алгоритмах комп'ютерної графіки: в алгоритмі покриття області штриховкою, в алгоритмах визначення видності — рухомого та нерухомого екранів тощо. Нехай область, яку треба покрити штриховкою (рис. 1.7), задана масивами координат (x1,y2), (x2,y2) (і = 1, 2, 3, 4). Рівняння ланок, що обмежують область, дістанемо у вигляді (1.10) при i = 1, 2, 3, 4. Визначивши iнтервал, який пробігає параметр b у рівнянні (1.1) сім'ї ліній штриховки, задамо крок зміни b. На кожному кроці треба розв'язати систему чотирьох рівнянь (1.10) і (1.1). У результаті дістанемо координати точок I…IV. Підставимо у формули (1.14) замість х та у знайдені координати хnj та ynj. Матимемо
Якщо хі+1-хі= 0, то слід скористатися другою формулою з (1.15), а якщо уі+1-уі= 0, то - першою. У результаті для точок ІІ і ІІІ дістанемо значення s2 та s3 за межами інтервалу 0<s<1, тобто їх не враховують при визначенні того відрізка лінії штриховки що належить області.
Полярні параметри прямої. Відстань р початку координат від прямої (1.2) та кут між віссю Ох і відрізком перпендикуляра ОК (рис. 1.8) називають полярними параметрами прямої. Відстань р визначають за формулою
Кут t визначають не безпосередньо, а за допомогою функцій синуса та косинуса:
Умова паралельності прямих (1.7) випливає з формул (1.8) при D= 0: A1B2-B1A2 (1.18) Умова перпендикулярності прямих (1.7): A1A2+B1B2 =0 (1.19) Рівняння прямої, яка проходить через точку М(х1, у1) і перпендикулярна до прямої (1.2): А(у –у1)- В(х-х1)=0. (1.20) Відстань точки М (х1,у1) до прямої (1.2):
Якщо в цю формулу підставити координати початку 0(0.0), то відстань d матиме знак С, чим і пояснюється знак абсолютної величини. Точки, розміщені по той самий бік від прямої що й початок координат, дають той самий знак для d. Точки. розміщені по різні боки від прямої, дають протилежні знаки для d. Тому відстань d називають орієнтованою. Коло Задання площини та ліній Площина у просторі. Площину в прямокутних декартових координатах задають у неявній формі Ах + Ву + Сz+D=0. (1.83) Ця площина поділяє простір на два півпростори, які можна визначити коефіцієнтом
Для координат x1, y1, z1, будь-якої точки першого півпростору р=1, для точки, яка належить другому півпростору, р = 1, а якщо точка належить площині, то р = 0. У нарисній геометрії площину задають, проекціями її визначника: трьома точками. що не належать одній прямій: точкою та прямою, що не проходить через точку, двома перетинними прямими: двома паралельними прямими, плоскою фігурою; слідами. Від графічної форми задання будь-яким визначником доцільно перейти. Взявши на площині три неколінійні точки М0(х0, у0, z0), M1(x1, y2, z3), М2,(x2, y2, z2) та підставивши координати їх у формули для визначення коефіцієнтів А, В, С, D. Дістанемо
Як уже зазначалося окремим випадком задання площини є той, коли вона за своїм положенням відносно деякої координатної системи с площиною рівня. Ідея поширення класичних координатних систем спеціальними системами та склад спеціальних систем зумовлені піднесенням будь-якої площини (див. формулу (1.85)) до такої системи координат, в якій вона б була б площиною рівня. Реалізація цієї умови дає змогу в компактній формі задавати плоскі лінії у просторі, діставати рівняння ліній перетину поверхні з площиною: · задавати кінематичні поверхні з плоскою твірною; · розв'язувати позиційні задачі на цій поверхні; · використовуючи допоміжні січні площини загального (у термінах нарисної геометрії) положення. Зберігаючи позначення та узагальнюючи їх на тривимірний простір, надамо рівнянням вигляду
Завдяки введеним спеціальним системам координат та їхнім властивостям щодо піднесення будь-якої площини до такої системи, де вона є площиною рівня, з'являється практично доцільний спосіб задання прямої та плоскої кривої лінії у відповідній системі спеціальних координат виразами
або
Ці рівняння можна віднести до залежності прямокутних декартових координат від спеціальних. Застосовуючи рівняння інцидентності площин прямої чи плоскої кривої, визначимо тип системи та значення t за наведеним алгоритмом. Підставивши формули дістанемо параметричні рівняння прямої чи плоскої кривої. Функція для прямої мас вигляд
де k і b відіграють ту саму роль на площині t=const у декартовій прямокутній системі u0v, що й у системі xОу. Для кола радіуса r, координати центра якого в системі u0v є (a,b), функція має вигляд
Для цього самого кола функції (1.88) набувають вигляду
Розглянемо тепер форми задання ще одного класу просторових кривих: гвинтових та квазігвинтових ліній. Гвинтову циліндричну лінію задають функціями залежності прямокутних декар-тових координат від циліндричних або під узагальнених циліндричних координат, де
Якщо в циліндричній системі координат радіус гвинтової лінії дорівнює r, то в узагальненій циліндричній системі він дорівнює Квазігвинтовою називають лінію, що зі сталим кроком напинається на поверхню обертання. Квазігвинтова лінія в гіперболічних координатах задається функціями (1.92). Якщо u=c=0, то вона розміщена на конусі, якщо u=c¹0, то вона розміщена на однопорожнинному гіперболоїді. Задання поверхонь У неявній формі центральні поверхні обертання другого порядку задають, функцією
Залежно відзначень параметрів, що входять у рівняння (1.93), воно визначає: стиснений еліпсоїд (р = 1, q= 1, а > с); витягнутий еліпсоїд (р = 1,q=1, a < с); сферу (р = 1,q=1, a = с); однопорожнинний гіперболоїд (р = -1,q=1); двопорожнинний гіперболоїд (р = -1,q = -1); конус (р = -1, q = 0). Після переходу згідно з залежністю до циліндричних координат та розв'язання рівняння відносно u дістанемо
або після підстановки u в рівняння матимемо рівняння цього класу поверхонь у параметричній формі:
Рівняння циліндра, вісь якого збігається з Оz, у неявній формі мас вигляд
а в параметричній формі ‑‑‑‑
Рівняння гіперболічного параболоїда в явній формі
Розглянемо інші класи поверхонь, що задають внутрішнім рівнянням у спеціальних координатах. Внутрішні рівняння класів та підкласів поверхонь в узагальнених циліндричних та гіперболічних координатах, як правило, збігаються. Внутрішні рівняння можна діставати в явній, неявній та параметричній формах. У параметричній формі параметр t є одним з функціональних параметрів, а другим параметром є інший, який відрізняється від змінних u та v. Для переходу до параметричної форми задання у прямокутних декартових координатах треба внутрішні рівняння підставити у формули, що виражають залежність прямокутних декартових координат від узагальнених циліндричних чи гіперболічних координат, Лінійчаті поверхні задають рівнянням
Внутрішні рівняння підкласів лінійчатих поверхонь дістають при певних значеннях функцій
то маємо поверхні однакового нахилу до площини хОу. Якщо то маємо поверхні з площиною паралелізму х0у. Якщо
то маємо однопорожнинний гіперболоїд обертання. Розгортні поверхні в узагальнених циліндричних координатах задають рівняннями
а в гіперболічних координатах — рівняннями
Внутрішні рівняння ребра обертання цієї поверхні знайдемо підстановкою u = 0 в рівняння (1.103) або (1.104) відповідно. Циліндр в узагальнених циліндричних координатах, однопорожнинний гіперболоїд у гіперболічних: u=c=const, v=v. (1.105) Гвинтові поверхні в узагальнених циліндричних та квазігвинтові поверхні в гіперболічних координатах: v=f(u)+kt. (1.106) Зокрема, якщо f(u) = bu(b=const), то маємо лінійчату поверхню v=bu+kt. (1.107) Розгортні гвинтові поверхні в узагальнених циліндричних координатах:
Розгортні квазігвинтові поверхні в гіперболічних координатах:
Циклічними називають поверхні, що утворюються колом. Якщо коло як твірна має сталий радіус, то циклічну поверхню називають трубчастою. Циклічну поверхню, циклічний каркас якої збігається із сім'єю ліній кривини, називають каналовою. Циклічні поверхні в неявній формі задають рівнянням
При j(t) = соnst маємо трубчаті поверхні:
Якщо
Якщо
Якщо
а якщо
Різьблену поверхню Монжа в узагальнених циліндричних координатах задають рівнянням
зокрема, циклічну
а гелікоїд
Багатогранні поверхні. Узагальнені циліндричні й гіперболічні координати застосовують відповідно для задання правильних призм і пірамід. Визначником правильної призми доцільно вважати: r—радіус вписаного в призму циліндра, який може бути внутрішнім параметром узагальненої циліндричної системи: tn — кутовий параметр однієї з граней (кут між площиною хОz та променевою площиною, що проходить через 0z і лінію дотику деякої грані призми та циліндра системи); h -- висота призми. При цьому вважають, що нижня основа призми лежить на площині х0у. а верхня па площині z= h; n -- кількість гранєй. Рівняння граней призми дістанемо у вигляді (1.87), надаючи t таких значень:
Якщо підставимо у рівняння (1.88) значення ti з рівняння (1.119) та
то матимемо рівняння ребер призми. Визначником пранильноїпірашди є: a -кут нахилу грані до осі Оz, що збігається з внутрішнім параметром гіперболічної системи, tn — кутовий параметр однієї з гра-ней (кут між площиною хОу і променевою площиною, що проходить через Оz. та лінію дотику деякої грані до конуса системи), h— висота піраміди. Вважають що вершина піраміди лежить у початку координат, а основа — на площині. Рівняння граней піраміди дістанемо у вигляді (1.88), надаючи t значення з рівняння (1.119). Рівняння ребер піраміди знайдемо як рівняння прямих, що проходять через дві точки S(0, 0, 0) та Аі (хі, уі, zi):
де xi, yi, визначають підстановкою значень ti з формули (1.119): v =-h та
Табл.1.2 Поверхні в ортогональних проекціях та в ізометрії ізометрії
Щодо побудови проекції обвидної, то в багатьох випадках це можна зробити, розв'язуючи рівняння (1.123) відносно однієї з дих змінних. Так для циліндра та конуса (див. табл. 1.1) обидва розв'язки не залежать від другої змінної, для центральних поверхонь другого порядку рівняння (1.123) є квадратним відносно лінійної змінної. Розв'язки цього рівняння використано також для каналової поверхні, різьбленої поверхні Монжа, катеноїда, псевдосфери. Для гранних поверхонь алгоритм визначення видимості полягає в порівнянні знаків лівої частини (1.123) для суміжних граней. Якщо Іі>0, Іі+1 > 0, (1.136) то ребро, по якому перегинаються ці грані, видиме; якщо Іі Іі+1 < 0, (1.137) то ребро контурне; якщо Іі<0, Іі+1 < 0, (1.138) то ребро невидиме. Моделювання розгорток До розгортних належать такі поверхні: багатогранники, циліндри, конуси та торси. Задача розгортування полягає в знаходженні функцій
або з урахуванням залежності прямокутних декартових координат точки на циліндрі чи конусі від відповідних спеціальних координат, в яких ці поверхні мають рівняння u=0,
У формулах (1.139) та (1.140) xp, yp -- декартові прямокутні координати на площині розгортки, x, y, z — декартові прямокутні координати точки, що належать розгортній поверхні. Циліндр. Для циліндра, радіус основи якого r формули (1.140) мають вигляд
Правильна призма. Нехай правильна n-гранна призма описана навколо циліндра радіуса r і має висоту h. Кутовий параметр однієї з вершин відносно площини визначимо через tH. Апофеми бічних граней призми мають узагальнену циліндрічну координату
Знайдемо
дістанемо таке значення j = 1, при якому ця умова виконується. Позначимо
Тоді координата u точки на поверхні призми в узагальненій ціліндричній системі виражається рівністю
 
Формули (1.141) мають вигляд
де v = z. Нагадаємо, що координати точки x, y, z на поверхні призми вважаємо заданими. Конус. У гіперболічних координатах рівнянням конуса є u = 0. Формули (1.140) набувають вигляду
де a — кут між віссю та твірною конуса. Правильна піраміда. Правильну піраміду віднесемо до вписаного в неї конуса. Кут a між його твірною та віссю входить до визначника піраміди. Як і для призми, tH — кутовий параметр однієї з вершин основи піраміди відносно площини х0z. Обчислимо ti за формулою (1.142), та р — за формулою (1.144), b та j — за формулою (1.143). Потім знаходимо:
Функції (1.140) мають вигляд
Па рис.1.23,1.28, наведено приклади програмної реалізації алгоритму визначення лінії взаємного перетину поверхонь та алгоритмів моделювання розгорток, На рис. 1.23 зображено конус і циліндр, які перетинаються. На рис.1.24 і рис. 1.26 подано розгортки конуса й циліндра відповідно з визначенням на розгортці лінії взаємного перетину. На рис. 1.27 показано два циліндри, які перетинаються, а на рис. 1.25 і рис. 1.28 — розгортки поверхонь циліндра з горизонтальною та вертикальною осями відповідно з визначенням на розгортці лінії перетину. Найменування ПГВ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ПАСГИ | М-2002 | ГФРНИ-1 | ИКГИ-0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Розмір робочої о поля, мм | 1000 х 1000 | 500 х 500 | 1055х780 | 850 х618 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Точність виміру координат, мм | 0,25 | 0.05 | 0,5 | 0,1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Продуктивність | - | 10мм/с | 3000 точок / год | 100мм/с |
Серед пристроїв для кодування найбільш поширеними с М-2002. М-2004. ЕМ-709. ГАРПИ-1, ПАСТИ. Мікроніка ДТ 2Ж1-А, а також пристрої фірм Саl Соmр, Веnson, Агіsto-Werke та ін. Основні характеристики деяких вітчизняних пристроїв графічного введення подано в табл. 1.3.
Для комп'ютерів, як правило, необхідна не просто копія зображення, а й інформація з певним змістом. Якщо інформацію було введено без розгляду, то виникає дуже складна проблема розпізнавання. Людина з напівавтоматичним планшетом спочатку не тільки відсортовує потрібну інформацію, а й може суто геометричні дані доповнювати командами, кодами та назвами, що вводяться з алфавітно-цифрової клавіатури. У зв'язку з цим широко застосовуються напівавтоматичні пристрої введення інформації з графічних документів, одним з яких є кодувальний планшет (дігітайзер). Наприклад, кодувальний планшет Мікроніка ДТ 2Ж0-А належить до напівавтоматичних пристроїв введення графічної інформації з креслень, ескізів, фотознімків та інших зображень.
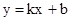 , (1.2)
, (1.2)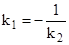 ) двох прямих з кутовими коефіцієнтами k1 та k2.
) двох прямих з кутовими коефіцієнтами k1 та k2.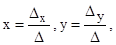 (1.8)
(1.8)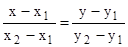 (1.9)
(1.9)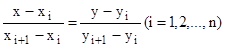 (1.10)
(1.10)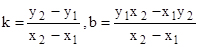 (1.11)
(1.11)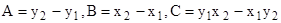 (1.12)
(1.12)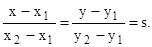 (1.13)
(1.13)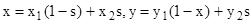 , (1.14)
, (1.14)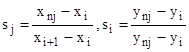 . (1.15)
. (1.15) . (1.16)
. (1.16)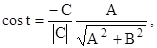
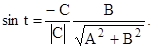 (22.17)
(22.17)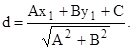 (1.21)
(1.21) . (1.84)
. (1.84) ,
,  ,
,  ,
, . (1.85)
. (1.85) (1.86)
(1.86)
 (1.87)
(1.87) (1.88)
(1.88) , (1.89)
, (1.89) . (1.90)
. (1.90) (1.91)
(1.91) (1.92)
(1.92) . В обох випадках крок гвинтової лінії становить. 2kp.
. В обох випадках крок гвинтової лінії становить. 2kp. (1.93)
(1.93) (1.94)
(1.94)
 (1.95)
(1.95) (1.96)
(1.96)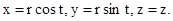 (1.97)
(1.97) (1.98)
(1.98) (1.99)
(1.99) та
та  . Якщо
. Якщо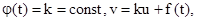 (1.100)
(1.100)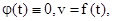 (1.101)
(1.101) (1.102)
(1.102) (1.103)
(1.103) (1.104)
(1.104) . (1.108)
. (1.108) . (1.109)
. (1.109)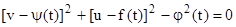 . (1.110)
. (1.110) . (1.111)
. (1.111) то дістаємо поверхні обертання:
то дістаємо поверхні обертання: . (1.112)
. (1.112) то маємо гвинтові чи квазігвинтові циклічні поверхні:
то маємо гвинтові чи квазігвинтові циклічні поверхні: . (1.113)
. (1.113)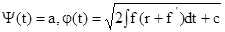 , то маємо каналові поверхні в узагальнених циліндричних координатах:
, то маємо каналові поверхні в узагальнених циліндричних координатах: , (1.114)
, (1.114) то каналові поверхні в гіперболічних координатах:
то каналові поверхні в гіперболічних координатах: . (1.115)
. (1.115) , (1.116)
, (1.116) (1.117)
(1.117) (1.118)
(1.118) . (1.119)
. (1.119) (1.120)
(1.120) (1.121)
(1.121) . (1.122)
. (1.122)








 , (1.139)
, (1.139) (1.140)
(1.140) (1,141)
(1,141) . (1.142)
. (1.142) а з умови
а з умови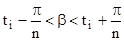 (1.143)
(1.143) (1.144)
(1.144) (1.145)
(1.145)





 , (1.146)
, (1.146) (1.147)
(1.147)
 . (1.148)
. (1.148)


