
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Площа та координати центра ваги плоскої фігури
Як відомо, площу елементарної фігури, обмеженої графіком у = f(x), віссю Ох та прямими x=c, x=d, визначають як
Координати центра ваги елементарної фігури:
де
статичний момент площі елементарної фігури відносно осі 0x;
статичний момент площі елементарної фігури відносно осі Оу. У формулах (1.79), (1.81) і (1.82) верхній знак відповідає f(x) > 0, a нижній - f(x) < 0. За умов розглядуваної задачі під плоскою фігурою розуміють плоску область, обмежену замкненими контурами, що не перетинаються між собою. Кожний контур є замкненою ламаною. Якщо деякі з контурів криволінійні, то вони заздалегідь з достатньою точністю апроксимуються ламаними. Вважатимемо, що вузли р контурів, які обмежують область, визначаються масивами координат хij, yij (i=1,2,…, mi; j=1,2,.., p) та умовами замкненості x1j= xmj, y1j=ymj. Отже, кожний контур містить nj=mj-1 вузлів, які не збігаються. Нехай також вузли обмежувальних контурів упорядковані так, що матеріальна площа лежить справа від напряму впорядкування. Тоді згідно з означенням плоскої фігури та прийнятими домовленостями знак перед правими частинами виразів (1.79), (1.81) і (1.82) можна опустити. Елементарною фігурою буде трапеція, а підінтегральною функцією — лінійна функція. ГЕОМЕТРИЧНЕ МОДЕЛЮВАННЯ У ПРОСТОРІ Задання площини та ліній Площина у просторі. Площину в прямокутних декартових координатах задають у неявній формі Ах + Ву + Сz+D=0. (1.83) Ця площина поділяє простір на два півпростори, які можна визначити коефіцієнтом
Для координат x1, y1, z1, будь-якої точки першого півпростору р=1, для точки, яка належить другому півпростору, р = 1, а якщо точка належить площині, то р = 0. У нарисній геометрії площину задають, проекціями її визначника: трьома точками. що не належать одній прямій: точкою та прямою, що не проходить через точку, двома перетинними прямими: двома паралельними прямими, плоскою фігурою; слідами. Від графічної форми задання будь-яким визначником доцільно перейти. Взявши на площині три неколінійні точки М0(х0, у0, z0), M1(x1, y2, z3), М2,(x2, y2, z2) та підставивши координати їх у формули для визначення коефіцієнтів А, В, С, D.
Дістанемо
Як уже зазначалося окремим випадком задання площини є той, коли вона за своїм положенням відносно деякої координатної системи с площиною рівня. Ідея поширення класичних координатних систем спеціальними системами та склад спеціальних систем зумовлені піднесенням будь-якої площини (див. формулу (1.85)) до такої системи координат, в якій вона б була б площиною рівня. Реалізація цієї умови дає змогу в компактній формі задавати плоскі лінії у просторі, діставати рівняння ліній перетину поверхні з площиною: · задавати кінематичні поверхні з плоскою твірною; · розв'язувати позиційні задачі на цій поверхні; · використовуючи допоміжні січні площини загального (у термінах нарисної геометрії) положення. Зберігаючи позначення та узагальнюючи їх на тривимірний простір, надамо рівнянням вигляду
Завдяки введеним спеціальним системам координат та їхнім властивостям щодо піднесення будь-якої площини до такої системи, де вона є площиною рівня, з'являється практично доцільний спосіб задання прямої та плоскої кривої лінії у відповідній системі спеціальних координат виразами
або
Ці рівняння можна віднести до залежності прямокутних декартових координат від спеціальних. Застосовуючи рівняння інцидентності площин прямої чи плоскої кривої, визначимо тип системи та значення t за наведеним алгоритмом. Підставивши формули дістанемо параметричні рівняння прямої чи плоскої кривої. Функція для прямої мас вигляд
де k і b відіграють ту саму роль на площині t=const у декартовій прямокутній системі u0v, що й у системі xОу. Для кола радіуса r, координати центра якого в системі u0v є (a,b), функція має вигляд
Для цього самого кола функції (1.88) набувають вигляду
Розглянемо тепер форми задання ще одного класу просторових кривих: гвинтових та квазігвинтових ліній. Гвинтову циліндричну лінію задають функціями залежності прямокутних декар-тових координат від циліндричних або під узагальнених циліндричних координат, де
Якщо в циліндричній системі координат радіус гвинтової лінії дорівнює r, то в узагальненій циліндричній системі він дорівнює Квазігвинтовою називають лінію, що зі сталим кроком напинається на поверхню обертання. Квазігвинтова лінія в гіперболічних координатах задається функціями (1.92). Якщо u=c=0, то вона розміщена на конусі, якщо u=c¹0, то вона розміщена на однопорожнинному гіперболоїді. Задання поверхонь У неявній формі центральні поверхні обертання другого порядку задають, функцією
Залежно відзначень параметрів, що входять у рівняння (1.93), воно визначає: стиснений еліпсоїд (р = 1, q= 1, а > с); витягнутий еліпсоїд (р = 1,q=1, a < с); сферу (р = 1,q=1, a = с); однопорожнинний гіперболоїд (р = -1,q=1); двопорожнинний гіперболоїд (р = -1,q = -1); конус (р = -1, q = 0). Після переходу згідно з залежністю до циліндричних координат та розв'язання рівняння відносно u дістанемо
або після підстановки u в рівняння матимемо рівняння цього класу поверхонь у параметричній формі:
Рівняння циліндра, вісь якого збігається з Оz, у неявній формі мас вигляд
а в параметричній формі ‑‑‑‑
Рівняння гіперболічного параболоїда в явній формі
Розглянемо інші класи поверхонь, що задають внутрішнім рівнянням у спеціальних координатах. Внутрішні рівняння класів та підкласів поверхонь в узагальнених циліндричних та гіперболічних координатах, як правило, збігаються. Внутрішні рівняння можна діставати в явній, неявній та параметричній формах. У параметричній формі параметр t є одним з функціональних параметрів, а другим параметром є інший, який відрізняється від змінних u та v. Для переходу до параметричної форми задання у прямокутних декартових координатах треба внутрішні рівняння підставити у формули, що виражають залежність прямокутних декартових координат від узагальнених циліндричних чи гіперболічних координат, Лінійчаті поверхні задають рівнянням
Внутрішні рівняння підкласів лінійчатих поверхонь дістають при певних значеннях функцій
то маємо поверхні однакового нахилу до площини хОу. Якщо то маємо поверхні з площиною паралелізму х0у. Якщо
то маємо однопорожнинний гіперболоїд обертання. Розгортні поверхні в узагальнених циліндричних координатах задають рівняннями
а в гіперболічних координатах — рівняннями
Внутрішні рівняння ребра обертання цієї поверхні знайдемо підстановкою u = 0 в рівняння (1.103) або (1.104) відповідно. Циліндр в узагальнених циліндричних координатах, однопорожнинний гіперболоїд у гіперболічних: u=c=const, v=v. (1.105) Гвинтові поверхні в узагальнених циліндричних та квазігвинтові поверхні в гіперболічних координатах: v=f(u)+kt. (1.106) Зокрема, якщо f(u) = bu(b=const), то маємо лінійчату поверхню v=bu+kt. (1.107) Розгортні гвинтові поверхні в узагальнених циліндричних координатах:
Розгортні квазігвинтові поверхні в гіперболічних координатах:
Циклічними називають поверхні, що утворюються колом. Якщо коло як твірна має сталий радіус, то циклічну поверхню називають трубчастою. Циклічну поверхню, циклічний каркас якої збігається із сім'єю ліній кривини, називають каналовою. Циклічні поверхні в неявній формі задають рівнянням
При j(t) = соnst маємо трубчаті поверхні:
Якщо
Якщо
Якщо
а якщо
Різьблену поверхню Монжа в узагальнених циліндричних координатах задають рівнянням
зокрема, циклічну
а гелікоїд
Багатогранні поверхні. Узагальнені циліндричні й гіперболічні координати застосовують відповідно для задання правильних призм і пірамід. Визначником правильної призми доцільно вважати: r—радіус вписаного в призму циліндра, який може бути внутрішнім параметром узагальненої циліндричної системи: tn — кутовий параметр однієї з граней (кут між площиною хОz та променевою площиною, що проходить через 0z і лінію дотику деякої грані призми та циліндра системи); h -- висота призми. При цьому вважають, що нижня основа призми лежить на площині х0у. а верхня па площині z= h; n -- кількість гранєй.
Рівняння граней призми дістанемо у вигляді (1.87), надаючи t таких значень:
Якщо підставимо у рівняння (1.88) значення ti з рівняння (1.119) та
то матимемо рівняння ребер призми. Визначником пранильноїпірашди є: a -кут нахилу грані до осі Оz, що збігається з внутрішнім параметром гіперболічної системи, tn — кутовий параметр однієї з гра-ней (кут між площиною хОу і променевою площиною, що проходить через Оz. та лінію дотику деякої грані до конуса системи), h— висота піраміди. Вважають що вершина піраміди лежить у початку координат, а основа — на площині. Рівняння граней піраміди дістанемо у вигляді (1.88), надаючи t значення з рівняння (1.119). Рівняння ребер піраміди знайдемо як рівняння прямих, що проходять через дві точки S(0, 0, 0) та Аі (хі, уі, zi):
де xi, yi, визначають підстановкою значень ti з формули (1.119): v =-h та
|
||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 189; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.165.66 (0.036 с.) |
 . (1.79)
. (1.79) (1.80)
(1.80) - (1.81)
- (1.81) (1.82)
(1.82) . (1.84)
. (1.84) ,
,  ,
,  ,
, . (1.85)
. (1.85) (1.86)
(1.86)
 (1.87)
(1.87) (1.88)
(1.88) , (1.89)
, (1.89) . (1.90)
. (1.90) (1.91)
(1.91) (1.92)
(1.92) . В обох випадках крок гвинтової лінії становить. 2kp.
. В обох випадках крок гвинтової лінії становить. 2kp. (1.93)
(1.93) (1.94)
(1.94)
 (1.95)
(1.95) (1.96)
(1.96)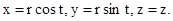 (1.97)
(1.97) (1.98)
(1.98) (1.99)
(1.99) та
та  . Якщо
. Якщо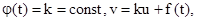 (1.100)
(1.100)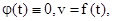 (1.101)
(1.101) (1.102)
(1.102) (1.103)
(1.103) (1.104)
(1.104) . (1.108)
. (1.108) . (1.109)
. (1.109)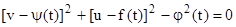 . (1.110)
. (1.110) . (1.111)
. (1.111) то дістаємо поверхні обертання:
то дістаємо поверхні обертання: . (1.112)
. (1.112) то маємо гвинтові чи квазігвинтові циклічні поверхні:
то маємо гвинтові чи квазігвинтові циклічні поверхні: . (1.113)
. (1.113)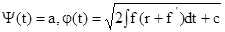 , то маємо каналові поверхні в узагальнених циліндричних координатах:
, то маємо каналові поверхні в узагальнених циліндричних координатах: , (1.114)
, (1.114) то каналові поверхні в гіперболічних координатах:
то каналові поверхні в гіперболічних координатах: . (1.115)
. (1.115) , (1.116)
, (1.116) (1.117)
(1.117) (1.118)
(1.118) . (1.119)
. (1.119) (1.120)
(1.120) (1.121)
(1.121) . (1.122)
. (1.122)


