
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямая и обратная геодезические задачиСодержание книги
Поиск на нашем сайте
XB – XA = ΔX; YB – YA = ΔY.
Разности ΔX и ΔY координат точек называют п р и р а щ е н и я м и к о о р д и н а т. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Из треугольника ABD следует, что
ΔX = d сos αAB; ΔY = d sin αAB. (2.9)
Приращения координат могут быть положительными и отрицательными, в зависимости от направления линий. Поскольку ось XX в геодезии совпадает с направлением меридиана, то можно составить таблицу для определения знака приращения координат (таблица 2.4).
Таблица 2.4 – Знаки приращений координат
Определив приращения координат по формулам (2.9), находят координаты второй точки В:
(2.10) YB = YA + ΔY = YA + d sinαAB.
Из формулы (2.10) следует правило для вычисления координат точки. Координаты последующей точки равны координатам предыдущей точки плюс соответствующее приращение координат. Приращения координат можно вычислять на микрокалькуляторе или по специальным таблицам.
Обратная геодезическая задача. В обратной геодезической задаче требуется определить длину линии АВ = d и ее направление (дирекционный угол αАВ) по заданным координатам точек А (XA, YA) и В (XB, YB) (см. рисунок 2.12). Согласно формулам (2.9) можно написать:
(2.11) d sinαAB = ΔY = YB – YA.
Разделив левые и правые части этих равенств, получим
tg αAB = (YB – YA) / (XB – XA) = ΔY / ΔX. (2.12)
Согласно (2.11) найдем:
(2.13) d = (YB – YA) / sinαAB = ΔY / sinαAB.
Из треугольника АВД (см. рисунок 2.12) получим контрольную формулу для d:
При определении α по формуле (2.12) согласно таблице 2.4 по знакам ΔX и ΔY определяют четверть, в которой находится угол, затем – румб линии АВ r = arctg ΔY/ΔX и по номеру четверти, используя формулы таблицы 2.3, – дирекционный угол αАВ.
9. Изображение земной поверхности на плоскости. Влияние кривизны Земли на горизонт. и вертикальн. расстояний
Для обработки результатов геодезических измерений и для получения топографических материалов точки земной поверхности проецируют отвесными линиями на поверхность более простую, чем земная.Такой поверхностью могут быть поверхности референц-эллипсоида, шара или плоскости. В геодезии используют проецирование точек линиями, перпендикулярными к поверхности относимости. Такое проектирование называют ортогональным. На рисунке 3.1 показано ортогональное проектирование контура ABCDE земной поверхности на поверхность референц-эллипсоида (см. рисунок 3.1, а) и плоскость (см. рисунок 3.1, б).
Рисунок 3.1 – Ортогональное проектирование
Как видно из рисунка 3.1, при ортогональном проектировании на референц-эллипсоид проекцией многоугольника ABCDE будет сферический многоугольник a'b'c'd'e', а при ортогональном проектировании многоугольника ABCDE на плоскость его проекцией будет плоский многоугольник abcde, который называют горизонтальной проекцией участка местности. Стороны плоского многоугольника ab, bc и т. д. являются горизонтальными проложениями соответствующих сторон пространственного многоугольника АВ, ВС и т. д. Как видно из рисунка 3.1, б горизонтальное проложение линии всегда меньше наклонной длины линии на местности.
d = D cosν,
где ν – угол наклона линии местности к плоскости Р. Углы abc, bcd и т. д. – являются горизонтальными проекциями соответствующих углов на местности и называются горизонтальными углами. Изучение формы и размеров сферической проекции фигуры местности является более сложным, чем изучение плоской проекции, кроме этого сферическую проекцию нельзя изобразить в подобном виде на плоскости из-за влияния кривизны Земли. Поэтому возникает вопрос, при каких расстояниях на земной поверхности кривизну уровенной поверхности Земли можно не учитывать или при каких расстояниях можно сферическую фигуру местности принимать за плоскую.
Участки земной поверхности размером 20×20 км можно считать плоскими, и в отношении расстояний, меньших 20 км, сферическую проекцию участков местности можно принимать за плоскую. Для линий, меньших 20 км можно не принимать во внимание влияние кривизны Земли при любых геодезических измерениях. При строительстве инженерных сооружений погрешности высотных измерений не должны превышать 1–2 мм, поэтому влияние кривизны Земли на определение высоты должно учитываться уже для расстояний более 100 м.
10. Топографические материалы: план, карта, профиль К топографическим материалам относятся: план, карта и профиль. Топографическим планом называют уменьшенное и подобное изображение на бумаге горизонтальных проекций участков местности. Как было показано выше, подобное изображение получают при ортогональном проецировании участков земной поверхности, не превышающих 20×20 км на горизонтальную плоскость. В уменьшенном виде на бумаге такое изображение называют планом местности. Изображение больших по размерам участков земной поверхности (более чем 20×20 км) на плоскость нельзя получить без искажений, т. е. с сохранением полного подобия. Такие участки ортогонально проецируют на поверхность референц-эллипсоида, а затем с поверхности эллипсоида по определенным математическим законам, называемым картографическими проекциями, переносят на плоскость. Полученное таким образом уменьшенное на бумаге изображение значительных участков земной поверхности (более 20 км) с учетом кривизны Земли называют картой. Карта, составленная в проекции Гаусса-Крюгера, называется топографической картой. На топографических планах и картах показывают ситуацию и рельеф местности. С и т у а ц и е й называют совокупность контуров и предметов местности. Ситуация является плановой частью местности (лес, луг, пашня, гидрография, здания, дороги, линии водопровода, гидротехнические объекты и т. д.). Ее изображают на планах и картах условными топографическими знаками. Р е л ь е ф о м называется совокупность неровностей земной поверхности. Рельеф – высотная часть местности. Она изображается на картах и планах в виде горизонталей – плавных кривых линий, проходящих через точки с равными высотами (отметками). Основные требования, предъявляемые к топографическим картам и планам, являются точность и наглядность. Под т о ч н о с т ь ю понимают соответствие местоположения, очертаний и размеров объектов на планах и картах действительности. Н а г л я д н о с т ь планов характеризуется зрительным восприятием образа земной поверхности, ее характерных черт и особенностей. Основными характеристиками точности планов и карт является масштаб, а наглядности – условные топографические знаки и цветовое оформление. Кроме планов и карт к топографическим материалам относятся профили местности, представляющие собой уменьшенное на бумаге изображение вертикального разреза поверхности Земли по заданному направлению. Профили местности являются топографической основой при составлении проектной документации, необходимой при строительстве железных и автомобильных дорог, линий водоснабжения и канализации и других коммуникаций.
11 – 12. Масштабы планов и карт. Точность масштаба При изображении участков земной поверхности на плане или карте размеры этих участков уменьшают в известное число раз. Степень уменьшения линий на плане по отношению к их горизонтальным проложениям (проекциям) на местности называется масштабом. Масштабы могут быть численные, линейные и поперечные. Ч и с л е н н ы м масштабом называется выражение в виде дроби числителем, которой является единица, а знаменателем – число, показывающее, во сколько раз линии на плане уменьшены по отношению к их горизонтальным проекциям на местности. Например, выражение 1: 2000 показывает, что в 1 см на плане содержится 2000 см (20 метров) местности. Зная численный масштаб плана, можно определить по длине линии местности соответствующую длину линии на плане и наоборот. Например, если длина линии на плане равна 3,23 см, а масштаб плана – 1:2000 то соответствующая линия на местности будет
d = 3,23 см × 2000 = 6460 см = 64,60 м.
Или, если длина линии на местности равна 200 м, то на плане масштаба 1:5000 длина соответствующего отрезка будет
l = 200 м: 5000 = 0,04 м = 4 см.
Для того чтобы не производить таких вычислений, обычно пользуются специальными графическими масштабами: линейным и поперечным. Для построения л и н е й н о г о масштаба берут прямую линию и на ней откладывают равные отрезки, называемые основанием масштаба (рисунок 3.3).
Для того чтобы расстояние по масштабу можно было откладывать более точно, строят п о п е р е ч н ы й масштаб. На прямой AF (рисунок 3.4) несколько раз откладывают основание масштаба (обычно 2 см) и из полученных точек восстанавливают к ней перпендикуляры. Один из перпендикуляров делят на 10 частей и через точки деления проводят линии, параллельные AF. Левый отрезок AO делят на 10 частей. Верхнее левое основание делят также на 10 равных частей. Точки верхнего и нижнего левых оснований соединяют наклонными линиями так, как показано на рисунке 3.4. Из рисунка 3.4 видно, что наименьшее деление поперечного масштаба
t = AO / 100 = 2 см / 100 = 0,2 мм.
Рисунок 3.4 – Поперечный масштаб
На рисунке 3.4 роспись поперечного масштаба сделана для численного масштаба 1:10000 при основании масштаба 2 см. Расстояния 466 и 730 м на поперечном масштабе отмечены точками ab и cd, в которые нужно установить ножки циркуля-измерителя. Невооруженным глазом отрезки на плане, меньше 0,1 мм становятся неразличимыми и практически являются точкой. Поэтому расстояние на местности, которое соответствует 0,1 мм на плане, принято называть точностью масштаба плана. В соответствии с этим точность стандартных численных масштабов топографических планов и карт приведена в таблице 3.1. Расчет выполнялся по формуле t = 0,1 мм · М,
где M – знаменатель масштаба.
Таблица 3.1 – Точность масштабов топографических планов и карт
Из приведенных данных видно, что чем меньше величина знаменателя численного масштаба, тем крупнее масштаб плана или карты и тем выше его точность. Точность масштаба позволяет определить, какие предметы местности могут быть изображены на плане или карте в виде подобной фигуры, а какие за малостью своих размеров обратятся на плане в точку. Например, здание длиной и шириной 5 м в масштабе 1:50000 изобразится на плане в виде одной точки. Важное практическое значение имеет и обратный вопрос: в каком масштабе нужно составлять план, чтобы определенные предметы местности были изображены на этом плане с сохранением подобия? На этот вопрос можно ответить, если проанализировать точность масштаба согласно таблице 3.1. При этом нужно иметь в виду, что наименьший отрезок на плане, который мы различаем как отрезок, а не как точку, равен 0,2 мм. Поэтому, например, для масштаба 1:2000 мы можем различить предметы местности, которые не менее 0,2 мм на плане, что соответствует 0,4 м на местности.
11 – 12. Масштабы планов и карт. Точность масштаба При изображении участков земной поверхности на плане или карте размеры этих участков уменьшают в известное число раз. Степень уменьшения линий на плане по отношению к их горизонтальным проложениям (проекциям) на местности называется масштабом. Масштабы могут быть численные, линейные и поперечные. Ч и с л е н н ы м масштабом называется выражение в виде дроби числителем, которой является единица, а знаменателем – число, показывающее, во сколько раз линии на плане уменьшены по отношению к их горизонтальным проекциям на местности. Например, выражение 1: 2000 показывает, что в 1 см на плане содержится 2000 см (20 метров) местности. Зная численный масштаб плана, можно определить по длине линии местности соответствующую длину линии на плане и наоборот. Например, если длина линии на плане равна 3,23 см, а масштаб плана – 1:2000 то соответствующая линия на местности будет
d = 3,23 см × 2000 = 6460 см = 64,60 м.
Или, если длина линии на местности равна 200 м, то на плане масштаба 1:5000 длина соответствующего отрезка будет
l = 200 м: 5000 = 0,04 м = 4 см.
Для того чтобы не производить таких вычислений, обычно пользуются специальными графическими масштабами: линейным и поперечным. Для построения л и н е й н о г о масштаба берут прямую линию и на ней откладывают равные отрезки, называемые основанием масштаба (рисунок 3.3).
Для того чтобы расстояние по масштабу можно было откладывать более точно, строят п о п е р е ч н ы й масштаб. На прямой AF (рисунок 3.4) несколько раз откладывают основание масштаба (обычно 2 см) и из полученных точек восстанавливают к ней перпендикуляры. Один из перпендикуляров делят на 10 частей и через точки деления проводят линии, параллельные AF. Левый отрезок AO делят на 10 частей. Верхнее левое основание делят также на 10 равных частей. Точки верхнего и нижнего левых оснований соединяют наклонными линиями так, как показано на рисунке 3.4. Из рисунка 3.4 видно, что наименьшее деление поперечного масштаба
t = AO / 100 = 2 см / 100 = 0,2 мм.
Рисунок 3.4 – Поперечный масштаб
На рисунке 3.4 роспись поперечного масштаба сделана для численного масштаба 1:10000 при основании масштаба 2 см. Расстояния 466 и 730 м на поперечном масштабе отмечены точками ab и cd, в которые нужно установить ножки циркуля-измерителя. Невооруженным глазом отрезки на плане, меньше 0,1 мм становятся неразличимыми и практически являются точкой. Поэтому расстояние на местности, которое соответствует 0,1 мм на плане, принято называть точностью масштаба плана. В соответствии с этим точность стандартных численных масштабов топографических планов и карт приведена в таблице 3.1. Расчет выполнялся по формуле t = 0,1 мм · М,
где M – знаменатель масштаба.
Таблица 3.1 – Точность масштабов топографических планов и карт
Из приведенных данных видно, что чем меньше величина знаменателя численного масштаба, тем крупнее масштаб плана или карты и тем выше его точность. Точность масштаба позволяет определить, какие предметы местности могут быть изображены на плане или карте в виде подобной фигуры, а какие за малостью своих размеров обратятся на плане в точку. Например, здание длиной и шириной 5 м в масштабе 1:50000 изобразится на плане в виде одной точки. Важное практическое значение имеет и обратный вопрос: в каком масштабе нужно составлять план, чтобы определенные предметы местности были изображены на этом плане с сохранением подобия? На этот вопрос можно ответить, если проанализировать точность масштаба согласно таблице 3.1. При этом нужно иметь в виду, что наименьший отрезок на плане, который мы различаем как отрезок, а не как точку, равен 0,2 мм. Поэтому, например, для масштаба 1:2000 мы можем различить предметы местности, которые не менее 0,2 мм на плане, что соответствует 0,4 м на местности.
13. Разграфка и номенклатура топографических планов и карт
Границами листов топографических карт с востока и запада служат меридианы, а с севера и юга – параллели. Они образуют рамки листов карт, имеющих форму равносторонних трапеций. Деление листа карты одного масштаба на листы карты более крупного масштаба называют разграфкой. Для удобства пользования многолистными картами введена система обозначения (нумерация) отдельных листов, называемая номенклатурой карт и планов. В основу номенклатуры карт положена международная разграфка листов карты масштаба 1:1000000, которые ограничены меридианами и параллелями и имеют размеры по широте 4о (ряды), а по долготе–6о (колонны). Ряды обозначаются заглавными буквами латинского алфавита от A до V к северу и югу от экватора, а колонны нумеруются арабскими цифрами от 1 до 60. Номера колонн считаются от меридиана с долготой 180о с запада на восток. Номера колонн и шестиградусных зон координат Гаусса-Крюгера отличаются на 30. Например, лист карты масштаба 1:1000000, на котором находится г. Москва, расположенный в 7-й зоне, имеет номенклатуру N-37. Разграфка более крупных масштабов топографических карт и планов, указанных в таблице 3.1, установлена с соблюдением следующих условий: - границами карт служат меридианы и параллели; - размеры листов карты должны быть удобными для издания и практического пользования; - лист карты масштаба 1:1000000 должен делиться на целое число карт более крупного масштаба; - номенклатура листов карт включает номенклатуру карты масштаба 1:1000000, а для карт масштаба 1:50000 и крупнее – номенклатуру листа карты 1:100000. Таким образом, одному листу карты масштаба 1:1000000 соответствуют: - 4 листа карты масштаба 1:500000, обозначаемые буквами А, Б, В, Г, и номенклатура этих листов имеет вид, например, N-37-Б; - 36 листов карты масштаба 1:200000, обозначаемые римскими цифрами І, ІІ, ІІІ, …, ХХХVI; номенклатура листов этой карты пишется в виде N-37-ХХХVI; - 144 листа карты масштаба 1:100000, обозначаемые арабскими цифрами от 1 до 144. Например: N-37-144. Одному листу карты 1:100000 соответствует 4 листа карты масштаба 1:50000, обозначаемых буквами А, Б, В, Г, и номенклатура их имеет вид N-37-144-Б. Одному листу карты 1:50000 соответствуют 4 листа карты масштаба 1:25000, обозначаемые буквами а, б, в, г. Например: N-37-144-Б-г. Одному листу карты масштаба 1:25000 соответствует 4 листа карты масштаба 1:10000, обозначаемые арабскими цифрами 1, 2, 3, 4. Например: N-37-144-Б-г-4. Одному листу карты 1:100000 соответствует 256 листов плана масштаба 1:5000, листы которого обозначаются порядковыми номерами от 1 до 256, заключенными в скобках. Например: N -37-144-(256). Одному листу плана 1:5000 соответствует 9 листов плана масштаба 1:2000, которые обозначаются строчными буквами а, б, в, г, д, е, з, и, заключенными в скобки. Например: N-37-144-(256-и). Сводные данные о номенклатуре карт и планов, размеры их рамок и километровой сетки приведены в таблице 3.2.
Таблица 3.2 – Сводные данные о номенклатуре карт и планов
14. Условные знаки топографических планов и карт Для обеспечения требования наглядности топографических материалов и понимания содержания планов и карт разработана специальная система графического обозначения предметов местности, которая называется условными знаками. Условные знаки подразделяют на площадные, линейные, внемасштабные, пояснительные и специальные. П л о щ а д н ы е (контурные или масштабные) знаки применяют для заполнения контуров природных и сельскохозяйственных угодий, длина и ширина которых выражается в масштабе карты. Границы контуров показывают точечным пунктиром, внутри которых изображается условный знак, напоминающий предмет на данной площади. Например, лес изображается кружками, пески – точками и т. д. Л и н е й н ы м и условными знаками показывают объекты линейного характера (дороги, реки, ЛЭП и др.), длина которых выражается, а ширина не выражается в масштабе карты. У линейных знаков приводятся различные числительные характеристики, дополняющие сведения о предмете. Например, на шоссе показаны ширина проезжей части и общая ширина дороги. В н е м а с ш т а б н ы е условные знаки служат для изображения объектов, размеры которых не выражаются в масштабе карты (мосты, колодцы, километровые столбы и т. д.). П о я с н и т е л ь н ы е условные знаки представляют собой подписи, дающие характеристики и названия объектов, например длину и ширину мостов, породу лесных насаждений и др. Эти знаки проставляют на основных площадных, линейных и внемасштабных условных знаках. С п е ц и а л ь н ы е условные знаки применяют соответствующие ведомства при составлении специальных карт и планов этой отрасли, например трубопроводы коммуникаций (теплотрасса, водопровод и т. д.). Кроме условных знаков для большей наглядности изображения различных элементов топографических карт используют цвет: - для рек, озер, каналов, заболоченных участков – синий; - для лесов и садов – зеленый; - шоссейных дорог – красный; - железные дороги и остальная ситуация – черный; - коричневым цветом показываются горизонтали, характеризующие рельеф местности. Помимо цветов используются также тип шрифта, толщина букв, их высота и наклон при обозначении. Условные знаки для разных масштабов сведены в специальные сборники, издаваемые службами геодезии и картографии. Они обязательны для всех ведомств и организаций, занимающихся составлением планов, карт, топографической съемкой местности. Знание условных знаков необходимо для того, чтобы понимать содержание топографических материалов, уметь их “читать” и для получения нужных сведений. Для лучшего ознакомления с условными знаками на учебных топографических картах приведены основные их образцы.
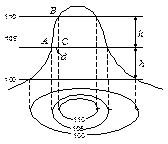
15, Рельеф местности и его изображение на планах и картах. Рельефом называют совокупность неровностей земной поверхности. Существует несколько способов изображения рельефа на топографических картах и планах. Наиболее старый способ – это изображение рельефа ш т р и х а м и, наносимым на карту по особой шкале. Рельеф местности может быть также изображен п о д п и с я м и отметок ряда точек или о т м ы в к о й к р а с к а м и различного тона. Однако наилучшим способом оказалось изображать рельеф г о р и з о н а л я ми в сочетании с некоторыми условными знаками и подписями отметок характерных точек. Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами. Существует п я т ь о с н о в н ы х ф о р м рельефа (рисунок 3.5): - возвышенность (рисунок 3.5, а); - котловина (рисунок 3.5, б); - хребет (рисунок 3.5, в); - лощина (рисунок 3.5, г); - седловина (рисунок 3.5, д). На рисунке 3.5 эти формы рельефа показаны в разрезе. Рассмотрим сущность изображения рельефа горизонталями. На рисунке 3.5, а показана возвышенность (холм, гора), наивысшую точку которой называют вершиной, низ – подошвой, а боковые поверхности – скатами. Для изображения возвышенности горизонталями представим себе, что эту возвышенность пересекают ряд равноотстоящих друг от друга плоскостей, параллельных основной уровенной поверхности. Линии пересечения этими плоскостями земной поверхности и будут являться горизонталями. Спроектировав их отвесными линиями на плоскость, получим на ней изображение возвышенности.
Расстояние между двумя соседними секущими плоскостями называют высотой сечения рельефа h. На картах и планах высота сечения рельефа характеризуется разностью высот двух смежных горизонталей. Например, на рисунке 3.5, а высота сечения рельефа h = 5 м. Расстояние между горизонталями на плане или карте называется заложением. На рисунке 3.5, а заложение d = АС. Зависимость между высотой сечения рельефа h, заложением d, углом наклона υ, уклоном i и линии местности АВ можно получить из треугольника АВС (рисунок 3.5, а):
i = h / d = tg υ. (3.6)
Уклон и угол наклона линии местности являются основными характеристиками крутизны скатов. Чем больше угол наклона, тем круче скат местности. Из формулы (3.6) следует, что чем меньше заложение d или чем чаще горизонтали на плане, тем скат местности круче. Изображение горизонталями котловины, лощины, хребта и седловины показано на рисунке 3.5. Котловина (впадина) – замкнутое углубление поверхности (см. рисунок 3.5, б). Самую низкую часть впадины называют дном, боковые поверхности – скатами, а линию слияния с окружающей местностью – бровкой.
Рисунок 3.5 – Основные формы рельефа
Хребет – вытянутая в одном направлении возвышенность с двумя скатами (см. рисунок 3.5, в). Линию встречи скатов в верхней части называют водоразделом (водораздельной линией). Лощина – вытянутое в одном направлении понижение с двумя скатами (рисунок 3.5 г). Линию встречи скатов в нижней их части называют водосливом или тальвегом (водосливной линией). Седловина – понижение между двумя возвышенностями (см. рисунок 3.5 д). Наиболее низкую точку между возвышенностями называют перевалом. Бергштрихи на картах и планах обычно показывают по водораздельным и водосливным линиям. Подписи на горизонталях делают так, чтобы основание числа показывало направление ската. Горизонтали вычерчивают коричневым цветом. Каждую десятую или пятую из них вычерчивают утолщенной линией.
16. Способы построения горизонталей по отметкам точек. Для проведения горизонталей на плане нужно нанести характерные точки, снятые на местности, и выписать их высоты. Те точки, между которыми земная поверхность не имеет переломов, т. е. имеет постоянный уклон, соединить линиями. Далее на каждой линии интерполированием находят точки пересечения ее горизонталями и отмечают высоты этих горизонталей. Соединив затем плавными кривыми линиями точки с одинаковыми высотами, получают изображение рельефа местности на плане. Таким образом, задача построения горизонталей на плане в основном сводится к умению находить проекции точек пересечения горизонталями линий, отметки концов которых известны, при этом высота сечения рельефа должна быть уже установлена. Эта задача называется и н т е р п о л и р о в а н и е м горизонталей, т. е. нахождением промежуточных значений высот горизонталей по отметкам точек. Интерполирование можно производить аналитическим или графическим способом. Аналитический способ. По известным высотам точек А и В и расстоянию d между ними (рисунок 3.6, а) необходимо найти величины расстояний d1 и d2 от точки А до точек М0 и N0 c отметками Нм и HN, равными отметкам горизонталей.
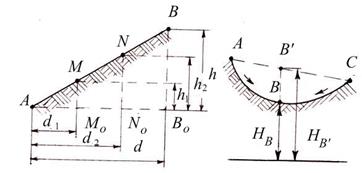
Рисунок 3.6 – Аналитический способ интерполирования
Из подобия треугольников АВВО, АММО и ANNO находим:
d1 = dh1 / h; d2 = dh2 / h,
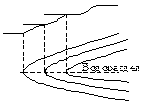
где h = HB – HA; h1 = HM – HA; h2 = HN – HA. На плане откладывают отрезки d1 и d2 и получают точки MO и NO, у которых подписывают их отметки. Следует отметить, что интерполирование горизонталей проводят только по линиям с равномерным скатом. На рисунке 3.6, б показан случай неправильной интерполяции между точками А и С с неравномерным скатом местности. Как видно из рисунка, вместо действительного положения точки В будет получена точка В' и соответственно вместо НВ будет получена неверная высота НВ'. Графический способ. Интерполирование этим способом выполняют с помощью миллиметровой или прозрачной бумаги. При наличии миллиметровой бумаги ее прикладывают к линии плана АВ. По отметкам концов АВ строят профиль этой линии. Проектируя затем на линию плана точки пере
17. Изображение рельефа Горизонталями и их свойства Рельефом называют совокупность неровностей земной поверхности. наилучшим способом оказалось изображать рельеф г о р и з о н а л я ми в сочетании с некоторыми условными знаками и подписями отметок характерных точек. Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами. Существует п я т ь о с н о в н ы х ф о р м рельефа (рисунок 3.5): возвышенность (рисунок 3.5, а); - котловина (рисунок 3.5, б); - хребет (рисунок 3.5, в); - лощина (рисунок 3.5, г); - седловина (рисунок 3.5, д). На рисунке 3.5 эти формы рельефа показаны в разрезе. Рассмотрим сущность изображения рельефа горизонталями. На рисунке 3.5, а показана возвышенность (холм, гора), наивысшую точку которой называют вершиной, низ – подошвой, а боковые поверхности – скатами. Для изображения возвышенности горизонталями представим себе, что эту возвышенность пересекают ряд равноотстоящих друг от друга плоскостей, параллельных основной уровенной поверхности. Линии пересечения этими плоскостями земной поверхности и будут являться горизонталями. Спроектировав их отвесными линиями на плоскость, получим на ней изображение возвышенности. Для наглядности некоторые горизонтали подписывают, кроме того у них ставят черточки-бергштрихи, показывающие направление ската местности. Расстояние между двумя соседними секущими плоскостями называют высотой сечения рельефа h. На картах и планах высота сечения рельефа характеризуется разностью высот двух смежных горизонталей. Например, на рисунке 3.5, а высота сечения рельефа h = 5 м. Расстояние между горизонталями на плане или карте называется заложением. На рисунке 3.5, а заложение d = АС. Зависимость между высотой сечения рельефа h, заложением d, углом наклона υ, уклоном i и линии местности АВ можно получить из треугольника АВС (рисунок 3.5, а):
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 668; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.017 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

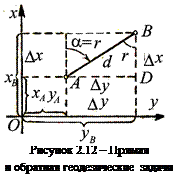 Прямая геодезическая задача используется для определения координат точек на местности. Пусть известны координаты начальной точки (XA, YA), дирекционный угол линии αАВ и расстояние между точками dАВ. Тогда по этим данным можно определить координаты второй точки В (рисунок 2.12). Согласно рисунку 2.12 имеем:
Прямая геодезическая задача используется для определения координат точек на местности. Пусть известны координаты начальной точки (XA, YA), дирекционный угол линии αАВ и расстояние между точками dАВ. Тогда по этим данным можно определить координаты второй точки В (рисунок 2.12). Согласно рисунку 2.12 имеем: ХВ = ХА + ΔХ = ХА + d cosαАВ;
ХВ = ХА + ΔХ = ХА + d cosαАВ; d cosαAB = ΔX = XB – XA;
d cosαAB = ΔX = XB – XA;  d = (XB – XA) / cosαAB = ΔX / cosαAB;
d = (XB – XA) / cosαAB = ΔX / cosαAB; 
 d = √ ΔX2 + ΔY2 = √ (XB – XA)2 + (YB – YA)2. (2.14)
d = √ ΔX2 + ΔY2 = √ (XB – XA)2 + (YB – YA)2. (2.14)
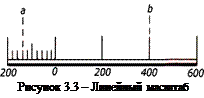 Левый крайний отрезок делят на 10 равных частей. Рассчитав по численному масштабу длину линии местности, соответствующую основанию масштаба, подписывают деления линейного масштаба. На рисунке 3.3 основание масштаба взято 2 см. При численном масштабе 1:10000 2 см на плане соответствует 200 м на местности. Следовательно, на линейном масштабе отрезки справа от нуля будут соответствовать 200 м на местности, а влево по 20 м. Для того чтобы отложить на плане линию, равную 540 м на местности нужно с помощью циркуля-измерителя отложить отрезок ab (см. рисунок 3.3). Как видно, отрезки меньше 2 мм в данном масштабе оцениваются на глаз.
Левый крайний отрезок делят на 10 равных частей. Рассчитав по численному масштабу длину линии местности, соответствующую основанию масштаба, подписывают деления линейного масштаба. На рисунке 3.3 основание масштаба взято 2 см. При численном масштабе 1:10000 2 см на плане соответствует 200 м на местности. Следовательно, на линейном масштабе отрезки справа от нуля будут соответствовать 200 м на местности, а влево по 20 м. Для того чтобы отложить на плане линию, равную 540 м на местности нужно с помощью циркуля-измерителя отложить отрезок ab (см. рисунок 3.3). Как видно, отрезки меньше 2 мм в данном масштабе оцениваются на глаз.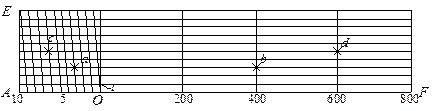

 а)
а)
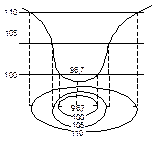 б)
б)
 в)
в)
 г)
г)


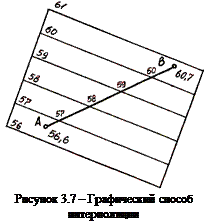 сечения линии профиля с линиями миллиметровой бумаги, принятыми за секущие плоскости, получают искомые точки М и N. При наличии прозрачной бумаги (восковки, кальки), на ней предварительно наносят ряд равноотстоящих друг от друга параллельных линий, которым придают отметки секущих плоскостей. Восковку накладывают на план так, чтобы конечные точки линии плана заняли положение, соответствующее их отметкам между линиями восковки (рисунок 3.7). Далее точки пересечения линии плана с линиями восковки перекалывают на план. Это и будут искомые точки на плане.
сечения линии профиля с линиями миллиметровой бумаги, принятыми за секущие плоскости, получают искомые точки М и N. При наличии прозрачной бумаги (восковки, кальки), на ней предварительно наносят ряд равноотстоящих друг от друга параллельных линий, которым придают отметки секущих плоскостей. Восковку накладывают на план так, чтобы конечные точки линии плана заняли положение, соответствующее их отметкам между линиями восковки (рисунок 3.7). Далее точки пересечения линии плана с линиями восковки перекалывают на план. Это и будут искомые точки на плане.


