
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка точности в равноточных измерениях
Точность измерений - качество результата измерений, определяющее близость погреш. величины к точному значению, получение результата правильного при геодез. измерениях.
Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности. Находят вероятнейшее значение измеренной величины по формуле арифметической средины. Вычисляют отклонения каждого значения измеренной величины от значения арифметической средины. По формуле Бесселя вычисляют среднюю квадратическую ошибку одного измерения. По формуле вычисляют среднюю квадратическую ошубку арифмет средины. Если измеряют линейную величину, то подсчитывают относительную ошибку каждого измерения и арифметической средины. При необходимости подсчитывают предельную ошибку одного измерения, которая может служить допустимым значением ошибок аналогичных измерений.
m = √ [V 2] / (n – 1). где V- вероятнейшая погрешность, N – число измерений
Формула называется формулой Бесселя и имеет большое практическое значение. Она позволяет вычислять среднюю квадратическую погрешность по вероятнейшим уклонениям результатов измерений от арифметической средины.
В практике геод. работ часто возникает необходимость найти среднюю квадратическую ошибку функции, если известны средние квадратические ошибки её аргументов, и наоборот. Рассмотрим функцию общего вида F= f (x y z …. U) дге x y z – независимые аргументы, полученные из наблюдений или проектного расчета со средними квадратическими ошибками mx my mz соответственно. Из теории ошибок измерений известно что средняя квадратическая ошибка функции независимых аргументов равна корню квадратному из суммы квадратов произведений частных производных функций по каждому из аргументов на средние квадратические ошибки соответствующих аргументов.
28. Средняя квадратическая погрешность функции измерения величин В геодезии часто нужно определить точность не только самих измеренных величин, но и их функций. Например, горизонтальное проложение линии является функцией наклонности расстояния и угла наклона, площадь определяемая планиметром является функцией отсчетов по планиметру и т. д. Поэтому важно уметь вычислять средние квадратические погрешности функций.
Рассмотрим некоторые виды функций. 1 Функция суммы двух аргументов
φ = Х + Y, (4.19)
где Х и Y – независимо измеренные величины. Допустим, что каждая из этих величин измерялась n раз и каждое из измерений сопровождалось случайными погрешностями ΔХ и ΔY. Тогда и функция φ, вычисленная по формуле (4.19), будет иметь погрешность Δφ:
φ + Δφ = (X + ΔX) + (Y + ΔY) или Δφ = ΔХ + ΔY. (4.20)
Возведем равенство (4.20) в квадрат: Δ Таких равенств может быть получено n. Сложив их и разделив на n, получим [Δ На основании четвертого свойства случайных погрешностей величина [ΔX ΔY] как сумма случайных погрешностей будет стремиться к нулю. Тогда с учетом равенства (4.5) будем иметь: m Нетрудно убедиться, что формула (4.23) будет верна и для функции
φ = X –Y. (4.24)
Аналогично предыдущему можно доказать, что для функции суммы (разности) нескольких аргументов
φ = ±Х ± Y ± Z ± … ± U. (4.25)
Квадрат средней квадратической погрешности этой функции будет равен сумме квадратов средних квадратических погрешностей аргументов: m Если mX = mY = mZ = …=mU, а число измеренных величин X, Y, Z, …, U равно n, то
m т. е. средняя квадратическая погрешность суммы равноточно измеренных величин в √n раз больше средней квадратической погрешности отдельного измерения.
2 Функция линейного вида φ = КХ,
где К – постоянное число; Х – аргумент, полученный из измерений. Если Х будет измерен со случайной погрешностью ΔХ, то функция будет иметь случайную погрешность
Δφ = К ΔX. (4.29)
Измерив аргумент n раз, можно составить n уравнений (4.29), взять сумму их квадратов и разделить на n. После чего получим [Δ откуда
mφ = K mX. (4.31)
Аналогично предыдущему можно показать, что для функции
φ = ± K1X ± K2Y ± … ± KnU (4.32)
получим
Δφ = K1ΔX ± K2ΔY ± … ± KnΔU (4.33)
или m
3 Функция общего вида φ = f (X, Y, Z, …,U), (4.37)
где X, Y, Z, …,U – независимо измеренные величины. С учетом случайных погрешностей функция (4.37) примет вид
φ + Δφ = f (X + ΔX; Y + ΔY; Z + ΔZ; …; U + ΔU). (4.38)
Разложив функцию (4.38) в ряд Тейлора и ограничившись только первыми степенями случайных погрешностей, получим функцию
Δφ = (∂f/∂x) ΔX + (∂f/∂y) ΔY + (∂f/∂z) ΔZ + … + (∂f/∂u) ΔU, (4.39)
где (∂f/∂x), (∂f/∂y), …, (∂f/∂u) – частные производные, которые для функции (4.39) являются постоянными величинами. Как видно, функция (4.39) аналогична функции (4.33). Следовательно, квадрат ее средней квадратической погрешности
= (∂f/∂x ∙ mX)2 + (∂f/∂y ∙ mY)2 + (∂f/∂z ∙ mZ)2 + … + (∂f/∂u ∙ mU)2. (4.40)
29. Неравноточные измерения 30. Формула общей арифметической середины На практике часто производятся и неравноточные измерения, которые выполнены в различных условиях или приборами различной точности, различным числом приемов. В этом случае уже нельзя ограничиваться простым арифметическим средним, здесь надо учитывать степень надежности каждого результата измерений. Степень надежности результата измерения, выраженная числом, называется весом этого измерения. Чем надежнее результат, тем больше его вес. Пусть имеем ряд средних значений: L1, L2, …, Ln – одной величины, полученных из Р1, Р2, …, Рn отдельных измерений. Согласно формуле (4.4) произведение Li Pi будет равно сумме отдельных измерений li в данном ряду, а сумма всех измерений во всех рядах будет равна L1P1 + L2P2 + … + Ln Pn. Число всех измерений будет равно P1 + P2 +…+ Pn.
Отсюда по правилу арифметической средины получим среднее значение из всех рядов измерений:
Lo = (L1P1 + L2P2 + … + LnPn) / (P1 + P2 + … +Pn) = [LP] / [P]. (4.44)
Выражение (4.44) называется формулой весового среднего или общей арифметической середины. Здесь число измерений Р1, Р2,…, Рn в каждом ряду является весом средних результатов L1, L2, …, Ln, а сумма весов является весом общей арифметической средины Lo. Во всех случаях, когда известны результаты измерений и их веса, вероятнейшее значение измеренной величины вычисляют по формуле (4.44). Обозначим среднюю квадратическую погрешность одного измерения через μ, а средние квадратические погрешности величин L1,L2….Ln соответственно через m1, m2, …, mn. Тогда, согласно равенству (4.36), можем написать, что ___ __ __ m1 = μ / √ P1; m2 = μ / √ P2; …; mn = μ / √ Pn. (4.45)
Если в формуле (4.45) принять Pi = 1, то μ = mi. Отсюда следует, что μ является средней квадратической погрешностью измерения, вес которого равен единице или так называемой средней квадратической погрешности единицы веса. Из формул (4.45) получим: __ __ __ μ = m1 √ P1 = m2 √ P2 = … = mn √ Pn,. (4.46)
Из равенства (4.46) можно сделать вывод, что произведение всякой величины на корень квадратный из ее веса будет иметь вес, равный единице, что позволяет приводить неравноточные измерения к равноточным. Из формулы (4.45) можно получить также общее математическое выражение веса: Pi = μ2 / m
т. е. вес измерения обратно пропорционален квадрату его средней квадратической погрешности. В частном случае, когда μ2 = 1,
Pi = 1 / m Для вывода средней квадратической погрешности единицы веса обозначим истинные случайные погрешности величин L1, L2, …, Ln через Δ1, Δ2, …, Δn. Тогда для ряда __ __ __ L1√ P1; L2√ P2; …; Ln√ Pn
истинные погрешности будут __ __ ___
Δ1√ P1; Δ2√ P2; …; Δn√ Pn. (4.49)
Ряд (4.49) равноточный, так как согласно формулам (4.31) и (4.46) средние квадратические погрешности его составляющих __ mi√ Pi = μ. Для равноточных измерений погрешность μ можно получить по формуле Гаусса (4.5): ________ μ = √ [PΔ2] / n. (4.50)
По аналогии с формулой (4.50) можем написать выражение средней квадратической погрешности единицы веса через вероятнейшие погрешности Vi величины Li (уклонения величины Li от весового среднего Lo): ____________ μ = √ [PV2] / (n – 1). (4.51)
Как видно, формулы (4.50) и (4.51) являются соответственно формулами Гаусса и Бесселя для неравноточных измерений. Для вывода средней квадратической погрешности Мо общей арифметической середины Lo с весом [Р] и средней квадратической погрешности единицы веса μ воспользуемся соотношением (4.46): ___ ____ μ = Мо√ [Р], откуда Мо = μ / √ [Р]. (4.52)
П р и м е р. Получены два результата измерения одной и той же линии и известны их средние квадратические погрешности:
L1 = 175,46 м; m1 = ± 0,10 м; L2 = 175,24 м; m2 = ± 0,20 м;
Определить вероятнейшее значение длины линии и его среднюю квадратическую погрешность. По формуле (4.48), принимая μ = 1, определим веса результатов измерений:
Р1 = 1/m21 = 1/(0,10)2 = 100; Р2 = 1/m22 = 1/(0,20)2 = 25.
Затем по формуле (4.44) и (4.52) находим вероятнейшее значение длины линии и его среднюю квадратическую погрешность:
Lo = (L1P1 + L2P2) / (P1 + P2) = (175,46 ∙ 100 + 175,24∙25) / (100 + 25) = 175,42 м; __ ___ Мо = μ / √[Р] = 1/√125 ≈ 0,09 м. Тогда вероятнейшее значение длины линии будет
Lo = 175,42 м ± 0,09 м; 29. Неравноточные измерения 30. Формула общей арифметической середины В предыдущих разделах были рассмотрены равноточные измерения. Однако на практике часто производятся и неравноточные измерения, которые выполнены в различных условиях или приборами различной точности, различным числом приемов. В этом случае уже нельзя ограничиваться простым арифметическим средним, здесь надо учитывать степень надежности каждого результата измерений. Степень надежности результата измерения, выраженная числом, называется весом этого измерения. Чем надежнее результат, тем больше его вес. Пусть имеем ряд средних значений: L1, L2, …, Ln – одной величины, полученных из Р1, Р2, …, Рn отдельных измерений.
Согласно формуле (4.4) произведение Li Pi будет равно сумме отдельных измерений li в данном ряду, а сумма всех измерений во всех рядах будет равна L1P1 + L2P2 + … + Ln Pn. Число всех измерений будет равно P1 + P2 +…+ Pn. Отсюда по правилу арифметической средины получим среднее значение из всех рядов измерений:
Lo = (L1P1 + L2P2 + … + LnPn) / (P1 + P2 + … +Pn) = [LP] / [P]. (4.44)
Выражение (4.44) называется формулой весового среднего или общей арифметической середины. Здесь число измерений Р1, Р2,…, Рn в каждом ряду является весом средних результатов L1, L2, …, Ln, а сумма весов является весом общей арифметической средины Lo. Во всех случаях, когда известны результаты измерений и их веса, вероятнейшее значение измеренной величины вычисляют по формуле (4.44). Обозначим среднюю квадратическую погрешность одного измерения через μ, а средние квадратические погрешности величин L1,L2….Ln соответственно через m1, m2, …, mn. Тогда, согласно равенству (4.36), можем написать, что ___ __ __ m1 = μ / √ P1; m2 = μ / √ P2; …; mn = μ / √ Pn. (4.45)
Если в формуле (4.45) принять Pi = 1, то μ = mi. Отсюда следует, что μ является средней квадратической погрешностью измерения, вес которого равен единице или так называемой средней квадратической погрешности единицы веса. Из формул (4.45) получим: __ __ __ μ = m1 √ P1 = m2 √ P2 = … = mn √ Pn,. (4.46)
Из равенства (4.46) можно сделать вывод, что произведение всякой величины на корень квадратный из ее веса будет иметь вес, равный единице, что позволяет приводить неравноточные измерения к равноточным. Из формулы (4.45) можно получить также общее математическое выражение веса: Pi = μ2 / m
т. е. вес измерения обратно пропорционален квадрату его средней квадратической погрешности. В частном случае, когда μ2 = 1,
Pi = 1 / m Для вывода средней квадратической погрешности единицы веса обозначим истинные случайные погрешности величин L1, L2, …, Ln через Δ1, Δ2, …, Δn. Тогда для ряда __ __ __ L1√ P1; L2√ P2; …; Ln√ Pn
истинные погрешности будут __ __ ___ Δ1√ P1; Δ2√ P2; …; Δn√ Pn. (4.49)
Ряд (4.49) равноточный, так как согласно формулам (4.31) и (4.46) средние квадратические погрешности его составляющих __ mi√ Pi = μ. Для равноточных измерений погрешность μ можно получить по формуле Гаусса (4.5): ________ μ = √ [PΔ2] / n. (4.50)
По аналогии с формулой (4.50) можем написать выражение средней квадратической погрешности единицы веса через вероятнейшие погрешности Vi величины Li (уклонения величины Li от весового среднего Lo): ____________ μ = √ [PV2] / (n – 1). (4.51)
Как видно, формулы (4.50) и (4.51) являются соответственно формулами Гаусса и Бесселя для неравноточных измерений. Для вывода средней квадратической погрешности Мо общей арифметической середины Lo с весом [Р] и средней квадратической погрешности единицы веса μ воспользуемся соотношением (4.46): ___ ____ μ = Мо√ [Р], откуда Мо = μ / √ [Р]. (4.52)
П р и м е р. Получены два результата измерения одной и той же линии и известны их средние квадратические погрешности:
L1 = 175,46 м; m1 = ± 0,10 м; L2 = 175,24 м; m2 = ± 0,20 м;
Определить вероятнейшее значение длины линии и его среднюю квадратическую погрешность. По формуле (4.48), принимая μ = 1, определим веса результатов измерений:
Р1 = 1/m21 = 1/(0,10)2 = 100; Р2 = 1/m22 = 1/(0,20)2 = 25.
Затем по формуле (4.44) и (4.52) находим вероятнейшее значение длины линии и его среднюю квадратическую погрешность:
Lo = (L1P1 + L2P2) / (P1 + P2) = (175,46 ∙ 100 + 175,24∙25) / (100 + 25) = 175,42 м; __ ___ Мо = μ / √[Р] = 1/√125 ≈ 0,09 м. Тогда вероятнейшее значение длины линии будет
Lo = 175,42 м ± 0,09 м;
|
|||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 821; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.211 (0.111 с.) |
 = Δ
= Δ  + Δ
+ Δ  + 2ΔX ΔY. (4.21)
+ 2ΔX ΔY. (4.21)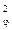 ] / n = [Δ
] / n = [Δ  ] / n + [Δ
] / n + [Δ  ] / n + 2[ΔXΔY] / n. (4.22)
] / n + 2[ΔXΔY] / n. (4.22) = m
= m  + m
+ m  . (4.23)
. (4.23) + m
+ m  +…+ m
+…+ m 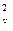 . (4.26)
. (4.26) = nm2 или mφ = m√ n, (4.27)
= nm2 или mφ = m√ n, (4.27) ] / n = K2 [Δ
] / n = K2 [Δ 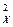 ] / n или m
] / n или m  = K2 m
= K2 m  = (K1mX)2 + (K2mY)2 + … + (KnmU)2. (4.34)
= (K1mX)2 + (K2mY)2 + … + (KnmU)2. (4.34)
 , (4.47)
, (4.47) . (4.48)
. (4.48) , (4.47)
, (4.47)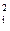 . (4.48)
. (4.48)


