
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы координат и высот, применяемые в геодезииСодержание книги
Поиск на нашем сайте
Координатами называют числа, определяющие положение точки земной поверхности относительно исходных линий или поверхностей. Система географических координат. Географические координаты могут быть геодезическими и астрономическими. Г е о д е з и ч е с к и е координаты определяют положение точки на поверхности референц-эллипсоида. В этой системе координатами являются широта и долгота точки, а исходными линиями – меридианы и параллели (рисунок 2.2). Если широты и долготы точки отнесены к поверхности геоида, то они называются а с т р о н о м и ч е с к и м и координатами Система плоских прямоугольных координат Гаусса - Крюгера. Данную систему используют при крупномасштабном изображении значительных частей земной поверхности. В проекции Гаусса-Крюгера обеспечивается сохранение подобного изображения фигур при переходе с поверхности земного эллипсоида на плоскость. Возникающие при этом искажения в размерах фигур достаточно малы и легко учитываются. В этой системе поверхность земного эллипсоида разграничивают меридианами через 6 или 3о по долготе на зоны. Нумерацию зон ведут от нулевого (Гринвичского) меридиана на восток. Число зон с долготой 6о составляет 60, а с долготой 3о – 120. Земной эллипсоид вписывают в цилиндр так, чтобы плоскость экватора совместилась с осью цилиндра (рисунок 2.3).
Рисунок 2.3 – Зональная система прямоугольных координат Гаусса-Крюгера
Местная система плоских прямоугольных координат. Эту систему координат применяют для определения координат точек, на небольших участках земной поверхности принимаемых за плоскость (не более 20 х 20 км). На плоскости берутся две взаимно-перпендикулярные линии, которые называются о с я м и к о о р д и н а т: ось абсцисс XX и ось ординат YY (рисунок 2.4). Точка пересечения их О служит началом координат. Направление оси абсцисс обычно принимают совпадающим с направлением меридиана. Координатами любой точки М будут являться длины перпендикуляров, опущенных из точки М на оси координат. Счет четвертей ведется от первой до четвертой по ходу часовой стрелки.
Система полярных координат. Эту систему применяют при определении положения точек на небольших участках земной поверхности, обычно при топо-
графических съемках местности или при разбивочных работах в строительстве.
Эта система используется для определения положения искусственных спутников Земли и ракет в трехмерной и космической геодезии. Сущность ее сводится к обработке геодезических измерений без проектирования их на уровенную поверхность Земли. Полученная система координат (OXYZ) участвует в суточном вращении Земли, оставаясь неподвижной пространственная система относительно точек земной поверхности, и по тому удобна для определения положения объектов земной поверхности.
|
||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.198.150 (0.009 с.) |



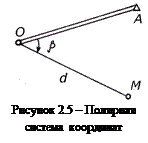 За начало координат в данной системе принимают точку О местности (рисунок 2.5), которую называют п о л ю с о м. За начальную координатную линию принимают п о л я р н у ю о с ь ОА, расположенную на местности произвольно или вдоль известной стороны. Полярными координатами любой точки М местности будут являться п о л я р н ы й у г о л (β) отсчитываемый от полярной стороны по ходу часовой стрелки и п о л я р н о е р а с с т о я н и е ОМ = d, определяемое как радиус-вектор.
За начало координат в данной системе принимают точку О местности (рисунок 2.5), которую называют п о л ю с о м. За начальную координатную линию принимают п о л я р н у ю о с ь ОА, расположенную на местности произвольно или вдоль известной стороны. Полярными координатами любой точки М местности будут являться п о л я р н ы й у г о л (β) отсчитываемый от полярной стороны по ходу часовой стрелки и п о л я р н о е р а с с т о я н и е ОМ = d, определяемое как радиус-вектор.  Система прямоугольных пространственных координат. В связи с применением спутниковых навигационных систем в геодезии начали применять систему прямоугольных пространственных координат (X, Y, Z). Начало ее находится в центре О земного эллипсоида, ось Z располагается вдоль полярной оси и направлена на Северный полюс Земли, ось X – в точку пересечения Гринвичского меридиана с экватором, а ось Y перпендикулярна оси X в плоскости экватора (рисунок 2.6).
Система прямоугольных пространственных координат. В связи с применением спутниковых навигационных систем в геодезии начали применять систему прямоугольных пространственных координат (X, Y, Z). Начало ее находится в центре О земного эллипсоида, ось Z располагается вдоль полярной оси и направлена на Северный полюс Земли, ось X – в точку пересечения Гринвичского меридиана с экватором, а ось Y перпендикулярна оси X в плоскости экватора (рисунок 2.6). 


