
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства функций, непрерывных на отрезке (теоремы Вейерштрасса и Больцано – Коши)Содержание книги
Поиск на нашем сайте
Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала. Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b. Теорема 1(Вейрштрасса). Функция, непрерывная на отрезке [ a, b ], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.
Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x2 и x 2'. Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области. Также теорема перестаёт быть верной для разрывных функций. Приведите пример. Следствие. Если функция f(x) непрерывна на [ a, b ], то она ограничена на этом отрезке.
18.Производная функции одной переменной. Основные определения. Геометрический и механический смысл.
Физический смысл производной: Производная показывает скорость изменения функции Геометрический смысл производной: Производная
|
||||||
|
Последнее изменение этой страницы: 2019-12-15; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.34 (0.005 с.) |

 Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [ a, b ], то найдётся хотя бы одна точка x1 Î [ a, b ] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x1) ≥ f(x). Аналогично найдётся такая точка x2, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x1) ≤ f(x).
Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [ a, b ], то найдётся хотя бы одна точка x1 Î [ a, b ] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x1) ≥ f(x). Аналогично найдётся такая точка x2, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x1) ≤ f(x).



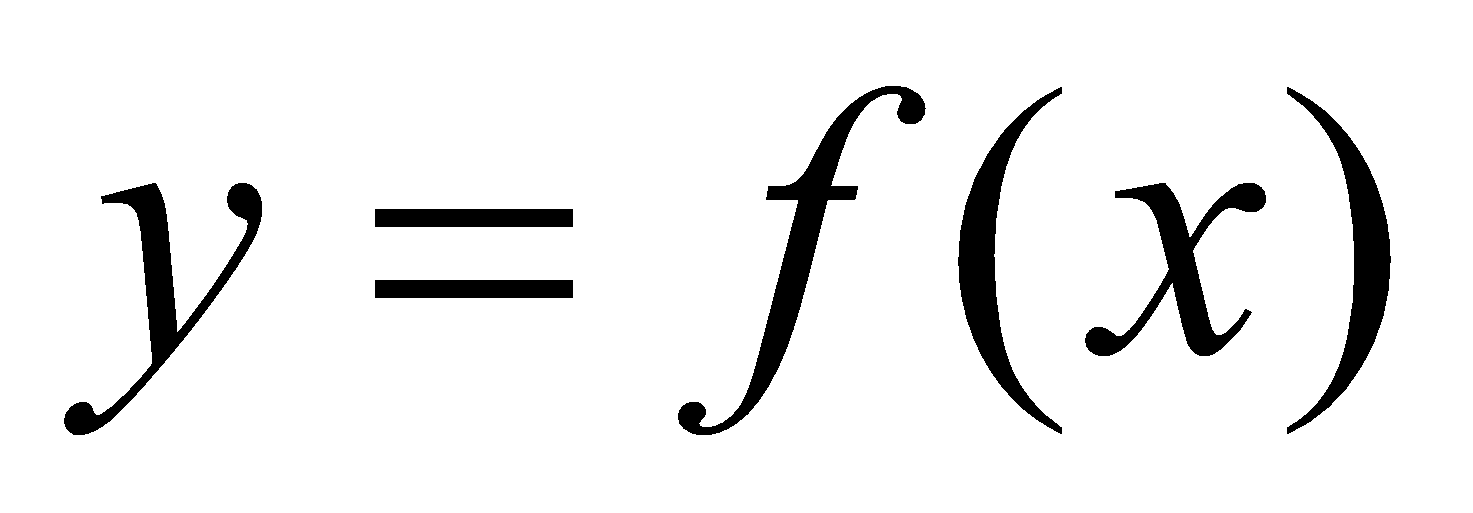 в зависимости от изменения аргумента x.
в зависимости от изменения аргумента x. в точке
в точке  равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции 


