Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции в точке. Односторонние пределы.Стр 1 из 6Следующая ⇒
Предел функции в точке. Односторонние пределы. Определение: Число «a» называется пределом функции «f» в точке x0, если для любого ε > 0 найдется δ = δ (ε) > 0 такое, что |x − x0| < δ, справедливо неравенство | f (x) − A| < ε
Односторонние пределы: 1)Предел слева Число A называется пределом функции Записывается так:
2)Предел справа Число A называется пределом функции Записывается так:
Предел функции в точке. Предел функции на бесконечности. *См.2 билет Предел функции на бесконечности: 2)Предел при Число A называется пределом функции Предел функции и его свойства. Дать опред. предела функции в точке и на бесконечности
4) Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций. Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций. 5) Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела:
6) Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
Расширенное свойство предела произведения Предел произведения нескольких функций равен произведению пределов этих функций:
7) Предел частного Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
Бесконечно большие функции. Связь с бесконечно малыми. Функция называется бесконечно большой в окрестности точки Функция называется бесконечно большой на бесконечности, если Теорема о связи между бесконечно большой и бесконечно малой функциями: Если функция
Доказательство: Пусть Эквивалентные бесконечно малые и их использование при вычислении пределов. Определение Если Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости. При · · · · · · · · · ·
Пример решения, заменой экв.: Найти Решение: Т.к.
Первый замечательный предел
Доказательство
Рассмотрим односторонние пределы Пусть Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке Очевидно, что:
(где
(из Подставляя в (1), получим:
Так как при
Умножаем на
Перейдём к пределу:
Найдём левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1. Следствия · · · · Доказательства
Второй замечательный предел:
13.Таблица экв.бесконечно малых. Вывод соотношений
14. Таблица экв.бесконечно малых. Вывод соотношений
Сравнение б.м..Таблица экв. Б. м. См. предыдущ. Билеты! Доказательство Так как ln y = v(x) ln u(x), то, продифференцировав это равенство, получаем
Теорема доказана. 31. Основные теоремы дифференциального исчисления. Теорема Ферма.
Правило Лопиталя.
Пусть a является некоторым конечным действительным числом или равно бесконечности. Если Если
Правило Лопиталя можно также применять к неопределенностям типа
Дифференциал длины дуги.
Предел вектор-функции Определение. Пусть Теорема. Пусть
Бол
Предел функции в точке. Односторонние пределы. Определение: Число «a» называется пределом функции «f» в точке x0, если для любого ε > 0 найдется δ = δ (ε) > 0 такое, что |x − x0| < δ, справедливо неравенство | f (x) − A| < ε
Односторонние пределы: 1)Предел слева Число A называется пределом функции Записывается так:
2)Предел справа Число A называется пределом функции Записывается так:
|
||||||
|
Последнее изменение этой страницы: 2019-12-15; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.96.61 (0.065 с.) |


 слева в точке
слева в точке  , если для любого положительного числа
, если для любого положительного числа 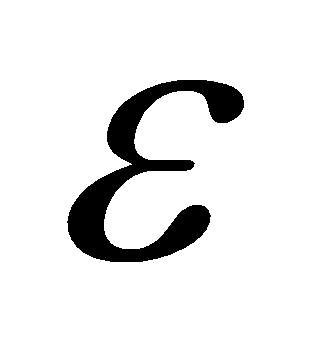 существует такое число
существует такое число  , что при
, что при 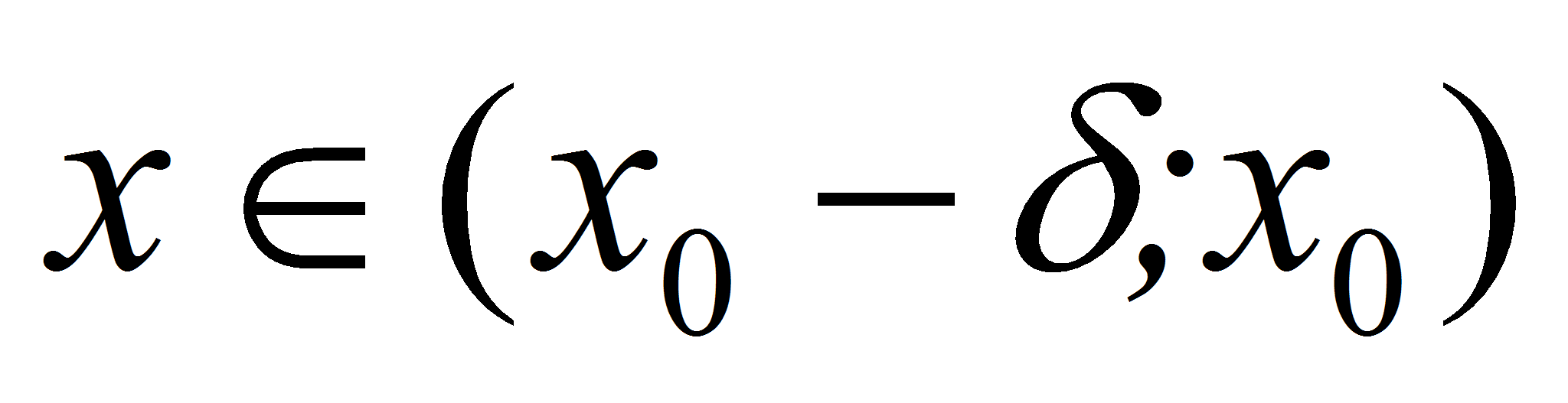 , выполняется неравенство
, выполняется неравенство  .
.
 , выполняется неравенство
, выполняется неравенство 
 :
: , если для любого положительного числа
, если для любого положительного числа  , что для всех
, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
.





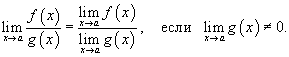
 , если
, если  .
. либо
либо  .
. - функция бесконечно малая (
- функция бесконечно малая ( ), то функция
), то функция  есть бесконечно большая функция и наоборот.
есть бесконечно большая функция и наоборот. , т.е.
, т.е.  . Тогда для любого числа
. Тогда для любого числа  существует такое число
существует такое число  , что для всех
, что для всех  , выполняется неравенство
, выполняется неравенство  , т.е.
, т.е.  , т.е.
, т.е.  , где
, где  . А из этого следует, что функция
. А из этого следует, что функция  - бесконечно большая.
- бесконечно большая. , то бесконечно малые величины
, то бесконечно малые величины  и
и  называются эквивалентными (
называются эквивалентными ( ).
). справедливы следующие соотношения эквивалентности (как следствия из так называемых замечательных пределов):
справедливы следующие соотношения эквивалентности (как следствия из так называемых замечательных пределов):



 , где
, где  ;
;
 , где
, где 

 , поэтому используют выражение:
, поэтому используют выражение: , где
, где 
 .
. и
и  при
при  , то:
, то:


 и
и  и докажем, что они равны 1.
и докажем, что они равны 1. . Отложим этот угол на единичной окружности (
. Отложим этот угол на единичной окружности ( ).
). . Точка H — проекция точки K на ось OX.
. Точка H — проекция точки K на ось OX. (1)
(1) — площадь сектора
— площадь сектора  )
)


 :
:  )
)
 :
:
 :
:





















 и
и  , то
, то  ;
; и
и  , то аналогично
, то аналогично  . Первые две неопределенности
. Первые две неопределенности  можно свести к типу
можно свести к типу  или
или  с помощью алгебраических преобразований. А неопределенности
с помощью алгебраических преобразований. А неопределенности  сводятся к типу
сводятся к типу  с помощью соотношения
с помощью соотношения




 ,
, 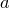 – предельная точка множества
– предельная точка множества  . Вектор
. Вектор  называется пределом вектор-функции
называется пределом вектор-функции  в точке
в точке  ,
,  .
. выбран базис и
выбран базис и  – координаты вектор-функции
– координаты вектор-функции  . Тогда утверждение
. Тогда утверждение