
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача максимального быстродействия. Колебательный объект 2 порядкаСодержание книги
Поиск на нашем сайте
Особенностью оптимального по быстродействию управления колебательными объектами является то, что на эти объекты не распространяется теорема об N интервалах. Другими словами, количество переключений зависит не только от порядка дифференциальных уравнений, но и от взаимного положения заданных начального и конечного состояний объекта управления. Подтверждение этой особенности управления колебательными объектами можно получить на основе принципа максимума. В соответствии с этим принципом оптимальное управляющее воздействие зависит от сопряженных переменных следующим образом: U0=sign(F(ksi1, ksi2, …)) Кроме того, известно, что в случае колебательных объектов управления сопряженные переменные, как функции времени, содержат гармонические составляющие, частоты которых равны частотам свободных колебаний объекта управления. Следовательно, по отношению к колебательным объектам 2 порядка принцип максимума позволяет сделать следующие выводы: - количество переключений знака управляющего воздействия может быть больше 1; - оптимальные по быстродействию траектории состоят из нескольких фрагментов, время движения по каждому из которых не может превышать половину периода свободных колебаний объекта управления. Построение оптимальных траекторий рассмотрим на примере консервативного колебательного звена 2 порядка.
Задаче максимального быстродействия для приведенного выше объекта управления соответствует следующий гамильтониан
Очевидно, что оптимальное управление зависит от сопряженных переменных следующим образом
Система сопряженных уравнений
Поскольку уравнения относительно сопряженных переменных не зависят от состояний объекта, выражение для
Полученное выражение для Для определения оптимальных моментов переключения можно использовать графический метод построения линий переключения в фазовом пространстве. На первом этапе построим фрагмент линии переключения первого порядка, который является траекторией движения объекта управления, приводящей его к конечному состоянию под действием постоянного управления. Эта операция может быть выполнена путем записи фазовой траектории движения объекта в обратном времени из заданного конечного состояния. Как следует из (8.1) длительность этого фрагмента не может превышать Описанный выше алгоритм построения линии переключения реализован в следующей MATLAB программе. В процессе выполнения расчетов оказалось, что солвер ode23s выполняет численное решение рассматриваемых дифференциальных уравнений гораздо точнее, чем солвер ode45 Файл Test8.m %Построение фрагмента линии переключения первого порядка % для положительного управления в обратном времени [t,x]=ode45('odefun8',[0 pi],[0 0]); plot(x(:,1),x(:,2),'r') hold on %Генерация координат точек фрагмента линии переключения второго % порядка %Искомые координаты вычисляются как координаты концов набора % траекторий, исходящих в обратном времени из фрагмента линии % переключения первого порядка под действием отрицательного управления %N - количество генерируемых точек global i N N=20; t=[]; x=[]; x1g=[]; x2g=[]; for i=1:N [t,x]=ode23s('odefun8_2',[0 pi*(i/N+1)],[0 0]); %Упаковка координат точек фрагмента второго порядка в отдельные % массивы x1g=[x1g x(length(t),1)]; x2g=[x2g x(length(t),2)]; end plot(x1g,x2g,'r') %За счет применения команды hold on настоящая программа отображает % фрагменты линии переключения первого и второго порядков
%Программа обеспечения поиска моментов переключения переводящих % объект из точки [-1 -4] в точку [0 0] %программа помогает выполнять ручной поиск моментов % переключения/отключения (t1, t2, T), ориентируясь на графики фрагментов % линии переключения global t1 t2 T t1=1.32; t2=4.46; T=6.5; t=[]; x=[]; [t,x]=ode23s('odefun8_3',[0 T],[-1 -4]); plot(x(:,1),x(:,2),'b') Файл odefun8.m function f=odefun8(t,x) f=[-(x(2));-(-x(1)+1)];
Файл odefun8_2.m function f=odefun8_2(t,x) global i N if t<=i*pi/N u=1; else u=-1; end f=[-(x(2));-(-x(1)+u)];
Файл odefun8_3.m function f=odefun8_3(t,x) global t1 t2 T if t<t1; u=1; elseif t<t2; u=-1; else u=1; end if t>T u=0; end f=[(x(2));(-x(1)+u)];
С помощью приведенной выше программы были получены следующие параметры оптимального прцесса:
Фазовая траектория оптимального процесса и графики фрагментов линии переключения показаны на рис. 8.1
Рис. 8.1. Фазовая траектория оптимального процесса Индивидуальные задания (по бригадам) По каждому варианту необходимо определить набор моментов переключения знака управляющего воздействия, который необходим для перевода объекта из начального в конечное состояние а также определить момент выключения управления. Модуль управляющего воздействия не может превосходить 1. Кроме определения моментов переключения необходимо построить графики фазовой траектории оптимального процесса и графики фрагментов линии переключения. Для всех вариантов уравнения объекта управления имеют следующий вид:
Приложение 1. Стандартные характеристические полиномы Общая форма полиномов (нормирование по базовой частоте
О динамических свойствах систем, имеющих рассматриваемые характеристические полиномы, можно судить по переходным характеристикам:
где 1. Биноминальные полиномы (Полиномы Ньютона)
Коэффициенты биноминального полинома степени
Полиномы Баттерворта Коэффициенты полинома Баттерворта степени
3. Полиномы, минимизирующие функционал Коэффициенты рассматриваемого полинома степени
4. Полиномы, минимизирующие функционал Коэффициенты рассматриваемого полинома степени
Приложение 2. Контрольные вопросы 1. Что является результатом аналитического решением дифференциального уравнения? 2. Что является результатом численного решения дифференциального уравнения? 3. Сколько решений имеет дифференциальное уравнение порядка 4. Приведите соответствия между оригиналами и L-изображениями основных функций, используемых при решении дифференциальных уравнений. 5. Чем отличаются статические и динамические задачи оптимизации? 6. Приведите основные особенности метода поиска, реализованного в MATLAB-функции FMINSEARCH. 7. Зависит ли результат работы функции FMINSEARCH от выбора начальной точки поиска и почему? 8. Сколько решений имеет задача поиска базовой частоты стандартного полинома, обеспечивающей минимальное время переходного процесса в линейной системе управления? 9. Как определяется время переходного процесса при решении задачи модального управления? 10. Какие этапы выполняются при решении задач оптимального управления на основе принципа максимума Л.С. Понтрягина? 11. В чем особенности применения принципа максимума Л.С. Понтрягина к решению задач на экономию управления? 12. Приведите общий вид выражения для управляющего воздействия как функции времени. (Имеется в виду задача экономии управления объектом, собственные числа которого вещественны и различны). 13. Что обычно является результатом решения задачи экономии управления численным методом на основании принципа максимума? 14. Сформулируйте задачу оптимизации расхода управления ориентированную на использование поисковых методов. 15. В чем особенности применения принципа максимума Л.С. Понтрягина к решению задач оптимального быстродействия? 16. Сформулируйте теорему об N интервалах. 17. Докажите, что теорема об N интервалах неприменима к объектам управления, собственные числа которых являются комплексными. 18. Начертите график функции времени, которая может быть решением задачи оптимального быстродействия для объекта управления 2 порядка, собственные числа которого вещественны и различны. 19. Начертите график функции времени, которая не может быть решением задачи оптимального быстродействия для объекта управления 2 порядка, собственные числа которого вещественны и различны. 20. Начертите график функции времени, которая не может быть решением задачи оптимального быстродействия для объекта управления 2 порядка, собственные числа которого являются комплексными числами. 21. Можно ли реализовать оптимальное по быстродействию управление в виде регулятора с обратными связями? 22. Что обычно является результатом решения задачи оптимального быстродействия численным методом на основании принципа максимума? 23. Сформулируйте задачу оптимального быстродействия, ориентированную на использование поисковых методов. 24. В чем особенности применения принципа максимума Л.С. Понтрягина к решению линейной квадратичной задачи? 25. Какие этапы выполнялись в процессе решения задачи оптимального быстродействия в лабораторной работе 7? 26. Опишите процесс построения линий переключения при выполнении лабораторной работы 8.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.108.134 (0.007 с.) |

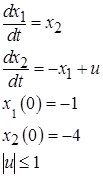



 может быть найдено из решения только системы сопряженных уравнений
может быть найдено из решения только системы сопряженных уравнений




 (8.1)
(8.1) показывает, что управляющее воздействие может иметь неограниченное количество переключений знака, но интервал постоянства знака не может превышать
показывает, что управляющее воздействие может иметь неограниченное количество переключений знака, но интервал постоянства знака не может превышать  секунд.
секунд. сек.,
сек.,  сек. и
сек. и  сек.
сек.









 ):
):

 - оператор обратного преобразования Лапласа.
- оператор обратного преобразования Лапласа.
 приведены в таблице.
приведены в таблице.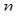


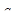








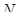 ?
?


