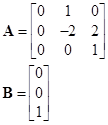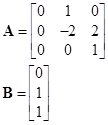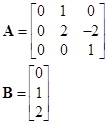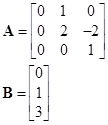Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическая задача оптимизацииСодержание книги
Поиск на нашем сайте
Под динамическими будем понимать задачи, в которых соотношения между параметрами и целевой функцией выражаются с помощью дифференциальных уравнений или функционалов от функций времени. В качестве первого примера рассмотрим следующую задачу: Задан динамический объект, описываемый дифференциальным уравнением;
Входным воздействием на объект является функция времени, содержащая неизвестный параметр Функция
Требуется найти такое значение параметра входного воздействия Строго говоря, приведенная задача не является задачей на нахождение минимума, но ее можно переформулировать как задачу минимизации при сохранении исходного смысла. Новая формулировка заключается в том, что мы потребуем найти такое значение параметра входного воздействия, которое обеспечит минимальное значение Решение поставленной задачи реализовано в MATLAB c помощью следующих скриптов: Файл Main7.m %В рассматриваемой программе решается задача поиска такого %значения um, которое соответствует минимальному значению %ABS(x) при t=4 %Для определения значения параметра um, программа вызывает %функцию поиска минимума (fminsearch) %Предполагается, что функция fmsfun7, на которую ссылается %fminsearch, вычисляет квадрат состояния объекта, %соответствующего моменту времени t=4 global t t1 x x0 u t1=2; x0=10; um=fminsearch(@fmsfun7,1) plot(t,x,t,u)
Файл fmsfun7.m %Основное назначение программы – вычислить квадрат значения %состояния объекта, соответствующего моменту времени t=4. %Для вычисления значений состояния объекта используется %функция %ode45 которая реализует метод численного решения %соответствующего дифференциального уравнения. %Функция odefun7, на которую ссылается ode45, предназначена %для вычисления значений правой части дифференциального %уравнения объекта. function f=fmsfun7(um) global t t1 x x0 u umax umax=um; t=[]; x=[]; u=[]; [t,x]=ode45(@odefun7,[0 2*t1],[x0]); for i=1:length(t), if t(i)<t1 u(i)=(um/t1)*t(i); else u(i)=-(um/t1)*t(i)+2*um; end end f=x(length(t))*x(length(t));
Файл odefun7.m function f=odefun7(t,x) global t1 umax if t<t1 u=(umax/t1)*t; else u=-(umax/t1)*t+2*umax; end f=-0.5*x+u; 2.3. Индивидуальные задания (по бригадам) Статическая задача. Определить глобальный максимум функции и исследовать поведение функции в районе экстремума.
Динамическая задача. Динамический объект
Входным воздействием на объект является функция времени, содержащая неизвестный параметр Функция
Модальное управление. Модальное управление имеет своей целью определение таких параметров регулятора, которые обеспечивают заданные значения корней характеристического уравнения замкнутой системы управления. Исходя из практики применения модального управления, были выбраны так называемые стандартные полиномы, распределение корней в которых удовлетворяет инженерным требованиям качества переходных процессов (полиномы Ньютона, Баттерворта и т.п.). Недостатком подхода к проектированию систем управления на основе стандартных полиномов является то, что, эти полиномы определены с точностью до базовой частоты, т.е. до масштабного коэффициента, характеризующего время протекания переходных процессов. Таким образом, для решения задачи модального управления необходимо не только выбрать желаемый характер переходных процессов (выбрать тип стандартного полинома), но и определить целесообразное значение базовой частоты для выбранного полинома. Устранить отмеченный недостаток можно путем вычисления базовой частоты в соответствии с экстремальным значением дополнительного показателя качества. Одним из таких показателей может быть время переходного процесса. Опора на время переходного процесса вполне конструктивна для реальных объектов управления, т.к. физически реализуемые объекты всегда содержат ограничения на максимальные значения параметров движения (скоростей, ускорений, сил, …) и, следовательно, их динамика существенно зависит от масштаба времени. Для примера рассмотрим следующую задачу: Для заданного объекта управления определить базовую частоту стандартного полинома, обеспечивающую минимум времени переходного процесса. Объект управления:
Закон управления:
На первом этапе решения задачи определяем характеристическое уравнение замкнутой системы, которая получается при использовании заданного закона управления объектом: Динамика замкнутой системы без учета ограничения на величину управления описывается следующей системой уравнений:
Характеристический полином замкнутой системы:
Сравнивая полученный характеристический полином замкнутой системы со стандартным полиномом 3 порядка
получаем систему уравнений для определения коэффициентов обратной связи:
На втором этапе требуется найти такое значение базовой частоты, которому соответствует минимальное значение времени переходного процесса в замкнутой системе управления, состоящей из объекта управления (3.1), управляемого по закону (3.2), параметры которого находятся из решения системы уравнений (3.3). Рассмотрим определение необходимого значения базовой частоты методом поиска «вручную». Для этого первоначально создадим MATLAB –программу, которая позволяет рассчитать время переходного процесса, соответствующего произвольно заданному значению базовой частоты. Эта программа состоит из двух скриптов:
Указание: Временем переходного процесса считается время после, которого измеряемая величина перестает выходить за пределы 5% от величины начального отклонения.
Файл main3.m %вектор коэфф-тов обратной связи K %и ограничение на управление um %объявлены глобальными для возможности передачи их в функцию odefun3 global K um um=1; %исследуемое значение базовой частоты om0=6; %начальное отклонение по x1 x10=1; %матрицы системы уравнений (3.3) A=[0 0 1; 0 2 2; 2 0 0]; b=[3*om0-3;3*om0^2-2;om0^3]; %решение системы уравнений (3.3) с помощью оператора «обратный слэш» K=A\b; %решение системы уравнений (3.1) и запись значений времени (t) %и соответствующих значений вектора состояния (x) в соответствующие %MATLAB - матрицы [t,x]=ode45('odefun3',[0 10],[x10 0 0]); %вычисление времени переходного процесса tm for i=length(t):-1:1 if abs(x(i,1))>0.05*x10 tm=t(i); break end end %отображение вычисленного значения времени переходного процесса %в окне команд MATLAB tm plot(t,x); Файл odefun3.m function f=odefun3(t,x) global K um %вычисление значения управляющего воздействия %в соответствии с законом управления u=-K(1)*x(1)-K(2)*x(2)-K(3)*x(3); %учет ограничения на величину управляющего воздействия if abs(u)>um u=um*sign(u); end %расчет вектора-столбца значений правых частей системы уравнений (3.1) f=[x(2);-2*x(2)+2*x(3);-x(3)+u]; Очевидно, что однократное выполнение скрипта main3.m позволяет вычислить время переходного процесса в исследуемой замкнутой системе, соответствующего заданному значению базовой частоты полинома Ньютона. Выполнение серии расчетов для разных значений базовой частоты позволяет выполнить поиск базовой частоты, обеспечивающей минимальное время переходного процесса. Организацию автоматического поиска базовой частоты с помощью функции FMINSEARCH предлагается выполнить студентам самостоятельно. Для этого целесообразно преобразовать файл-программу main.m в файл-функцию, у которой входным параметром является значение базовой частоты, а выходным – значение времени переходного процесса. Для запуска процесса поиска достаточно задать начальное значение базовой частоты и вызвать функцию FMINSEARCH, которая ссылается на разработанную ранее файл-функцию. Индивидуальные задания (по бригадам) По каждому варианту необходимо найти значение базовой частоты заданного типа полинома, обеспечивающее минимальное время переходных процессов в замкнутой системе управления и построить графики переходных процессов по состояниям объекта управления и управляющему воздействию. Для всех вариантов максимально допустимое значение управляющего воздействие принимается равным 1 и вектор начальных условий [1 0 0] Подробное описание стандартных полиномов См. приложение.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.57.239 (0.008 с.) |


 :
: является кусочно-линейной, и её вид определяется следующей таблицей значений;
является кусочно-линейной, и её вид определяется следующей таблицей значений;
 , при котором
, при котором  .
. . Такая постановка задачи позволяет использовать при решении поставленной задачи MATLAB – функцию FMINSEARCH. Кроме функции FMINSEARCH будет использована функция ODE45, которая предназначена для численного решения дифференциального уравнения.
. Такая постановка задачи позволяет использовать при решении поставленной задачи MATLAB – функцию FMINSEARCH. Кроме функции FMINSEARCH будет использована функция ODE45, которая предназначена для численного решения дифференциального уравнения.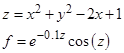












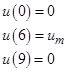
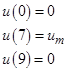

 (3.1)
(3.1) (3.2)
(3.2)
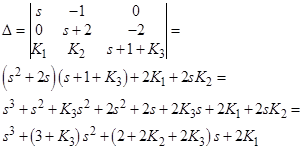

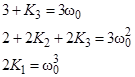
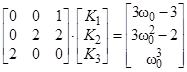 (3.3)
(3.3)