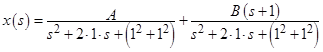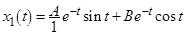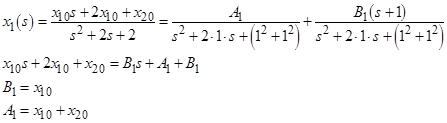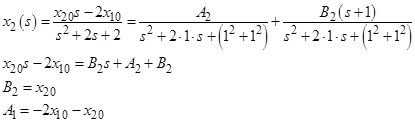Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналитическое и численное решение дифференциальных уравнений.
1.1 Аналитическое решение дифференциального уравнения 1 порядка методом преобразования Лапласа. Преобразованием Лапласа функции времени
Удобство использования этого преобразования для решения дифференциальных уравнений заключается в том, что после преобразования по Лапласу дифференциальные уравнения преобразуются в алгебраические. Причиной описанного изменения свойств дифференциальных уравнений при использовании преобразования Лапласа являются следующие следствия (1.1):
Таким образом, процесс решения дифференциального уравнения методом преобразования Лапласа заключается в выполнении следующих шагов: - преобразование исходного дифференциального уравнения в алгебраическое; - нахождение решения алгебраического уравнения; - определение решения дифференциального уравнения с помощью обратного преобразования Лапласа, применяемого к полученному ранее решению алгебраического уравнения. Под обратным преобразованием Лапласа понимается следующее соотношение:
При выполнении практических расчетов, требующих решения дифференциальных уравнений, используются таблицы преобразования Лапласа, которые позволяют выполнять операции прямого и обратного преобразований без выполнения операций интегрирования, предусмотренными выражениями (1.1) и (1.3) Для примера рассмотрим решение следующего дифференциального уравнения первого порядка:
После преобразования по Лапласу в соответствии с (1.2) получаем следующее алгебраическое уравнение:
Очевидно, что решением (1.4) является выражение (1.5)
Для получения оригинала
После применения табличного соотношения к нашему случаю получаем искомое решение дифференциального уравнения:
1.2. Аналитическое решение дифференциального уравнения 2 порядка методом преобразования Лапласа. Вещественные корни характеристического уравнения
В соответствии с таблицей преобразования Лапласа
Комплексные корни характеристического уравнения
Для удобства применения таблиц обратного преобразования Лапласа представим
слагаемые которой соответствуют следующим табличным выражениям:
что позволит представить
Использование описанного выше разложения на дроби позволяет получить следующие выражения:
|
|||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.187.233 (0.005 с.) |
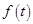 , называется функция
, называется функция 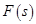 комплексной переменной
комплексной переменной 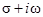 , такая что:
, такая что: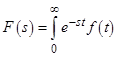 (1.1)
(1.1)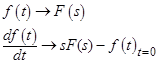 (1.2)
(1.2)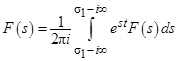 (1.3)
(1.3)
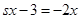 (1.4)
(1.4) (1.5)
(1.5)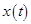 может быть использовано Следующее табличное соотношение:
может быть использовано Следующее табличное соотношение:

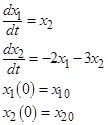
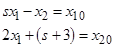
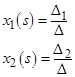
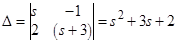

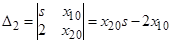
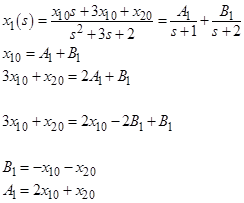
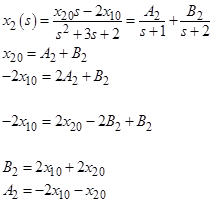

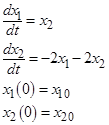
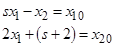

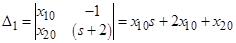

 в виде следующей суммы:
в виде следующей суммы: