
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Учитывая, что по закону ГукаСодержание книги
Поиск на нашем сайте
и обозначив Если Для определения реакций в связях основной системы применяются два способа: статический и аналитический. При статическом способе реакции во введённых связях определяются, используя метод сечений - составляя уравнение равновесия части расчётной схемы, содержащей конкретную связь. Этот способ рассмотрим на примере в п. 4.4.
4.1.3. Аналитический способ определения реакций в основной системе Рассмотрим фрагмент основной системы метода перемещений в виде одной балки II типа в двух состояниях: при В соответствии с принципом возможных перемещений (см.п.2.3), используя (2.12), (2.13) получим Единственным внешним силовым фактором в состоянии i, совершающим работу, является единичная реакция
Применяя к двум состояниям теорему о взаимности возможных работ (2.37), получим выражающее теорему о взаимности единичных реакций, которая приводит к симметричности коэффициентов Окончательно, имеем Следовательно, для вычисления реакции в связи основной системы с номером i от перемещения
Для вывода формулы грузовой реакции Соответственно состояние основной системы при единичном повороте введённой связи i на угол где системы, за которые приняты перемещения в состоянии Подставляя (4.10) и (4. 11) в (4.9), получим Отсюда где Это перемещение может быть найдено по формуле Мора Напомним, что суммирование проводится по всем участкам стержневой системы. В соответствии с (4.14) нужно построить две эпюры моментов:
Если умножить ординаты Остановимся подробнее на проблеме выбора системы для построения эпюры
а при перемножении эпюры
Выбрав систему, мы получим неверный результат, так как эта система не удовлетворяет требованию отсутствия связи по направлению Системы, обеспечивающие правильный результат и, статически определимые. Но это качество несущественно - если у нас есть готовая эпюра Эпюра изгибающих моментов для неё получена методом сил (расчет опускаем). При подстановке в (4.15) она даёт тот же результат, что и эпюры
Самым простым явилось применение системы Конечно, использование статически неопределимых систем для определения Подводя итог, приходим к выводу, что если систему для построения эпюры Таким образом, для вычисления грузовой реакции 1) Построить в основной системе метода перемещений эпюру изгибающих моментов 2) Выбрать из заданной системы геометрически неизменяемую статически определимую систему (так, как это делалось при расчёте по методу сил - путём отбрасывания n лишних существующих связей) и построить в ней эпюру 3) Перемножить обе эпюры под интегралом и взять результат с обратным знаком.
4.1.4. Статический способ вычисления реакций в основной системе метода перемещений и их аналитическая проверка на примере расчёта рамы Построить эпюру изгибающих моментов для рамы при действии на неё узловой горизонтальной силы Р =90 кН и равномерно распределённой нагрузки q =30 кH/м. Решение. 1. Устанавливаем степень кинематической неопределимости (4.1):
Для определения
Общее число связей достаточно для неизменяемости, но одна из вертикальных связей поставлена неверно - шарнир С соединён с “землёй“ двумя связями, лежащими на одной прямой. Система мгновенно изменяемая - возможно горизонтальное смещение диска ВС. Этот случай разобран в п. 4.1.1. и число линейных неизвестных 2. По направлению неизвестных устанавливаем дополнительные связи - образуем основную систему метода перемещений. В месте угла поворота 3. Записываем систему двух канонических уравнений метода перемещений по (4.6):
4. Вычисляем коэффициенты канонических уравнений. Для этого основную систему метода перемещений рассматриваем в трёх независимых состояниях, в каждом из которых строим эпюру моментов (учитываем только деформации изгиба). В первом состоянии плавающая заделка в узле С поворачивается на угол Во втором состоянии ригель смещается на величину В третьем состоянии основная система находится под действием заданной нагрузки при неподвижных опорных закреплениях. Эпюра Коэффициенты канонических уравнений будем определять статическим способом Коэффициент
Здесь же показываем искомую реакцию Составляем уравнение равновесия для узла
Коэффициент
Коэффициент
Видим, что по величине Коэффициент
Для определения свободных членов системы уравнений или “грузовых“ реакций рассматриваем третье состояние с эпюрой
Реакция в связи 2 от нагрузки q равна нулю
5. Проводим проверку правильности вычисления коэффициентов. Для этого воспользуемся формулами (4.8) и (4.15). Построим суммарную единичную эпюру в основной системе метода перемещений. Ординаты эпюры Вычислим интеграл типа (4.8)
Таким образом, если вычислить
С другой стороны Результаты совпали, следовательно, коэффициенты при неизвестных найдены верно. Далее вычислим интеграл типа (4.15)
С другой стороны Результаты совпали, следовательно, свободные члены системы уравнений найдены верно.
4.1.5 Продолжение расчёта рамы методом перемещений в матричной форме В дальнейшем конкретные вычисления для рамы будем сопровождать выводом формул для общего случая n раз кинематически неопределимой системы.
1. Размечаем начало и конец каждого участка рамы своим номером, выбираем правило знаков для ординат эпюр моментов для каждого участка - готовим схему рамы к расчёту в матричной форме (точно так же, как при расчёте по методу сил). Конечной целью расчёта является вычисление вектора 2. После выбора основной системы метода перемещений (для нашей рамы это сделано в п. 4.1.1) запишем вектор неизвестных 3. Записываем систему n канонических уравнений метода перемещений типа (4.6) в виде где 4. В основной системе строим эпюры моментов при нескольких состояниях: единичных (всего n) и грузовом (для нашего примера это уже сделано в п. 4.1.4 [4]). Все единичные эпюры, записанные в виде матриц столбцов, образуют матрицу влияния моментов (аналогично (3.9) в методе сил) Ординаты грузовой эпюры образуют вектор 5. Из заданной системы путём отбрасывания связей образуем статически определимую систему, в которой от нагрузки строим эпюру моментов, ординаты которой образуют вектор
6. Проведём вывод формул для вычисления матриц Сравнивая формулу для перемещений типа (3.7)
где Рассуждая аналогичным образом, вместо (4.15) в матричной форме будем иметь Далее весь вектор можно получить по формуле Формулы (4.25) и (4.27) получены для общего случая. В нашем примере мы получили коэффициенты системы уравнений статическим способом (см.п.4.1.4)
7. Решаем систему уравнений (4.20) с помощью обратной матрицы Обратная матрица для нашей системы имеет вид Проводя вычисления по (4.28), получим вектор перемещений Отрицательные величины перемещений свидетельствуют о том, что их направления не совпадают с выбранными в начале расчёта. 8. Окончательные значения изгибающих моментов в отмеченных сечениях рамы получим складывая эпюры от каждого Для нашей рамы без учёта стрелки (будет учтена при построении окончательной эпюры)
9. Проведём проверку правильности построения статическим способом. Вырежем узел С и в сечениях покажем изгибающие моменты. Составим уравнение равновесия Проведём деформационную проверку. Для этого превратим заданную систему в статически определимую, приложим в точке К силу
Погрешность составляет 10. Построим эпюру поперечных сил так же, как это делалось в п. 3.1.3 при расчёте рамы методом сил. Участок 1-2. Участок 5-6. Участок 7-8. Вырезаем участок 3-4 и из условий его равновесия определяем поперечные силы в крайних сечениях.
Проверка 11. Построим эпюру нормальных сил, рассматривая равновесие узлов рамы. Узел 2-3. Узел 4-6-7. Нормальные силы в крайних сечениях ригеля 3-4 одинаковы. Для вычисления двух значений Следовательно, задача определения нормальных сил является статически неопределимой и нужно составить уравнение деформаций вдоль стоек 5-6-7-8. Под действием растягивающих сил Подставим сюда выражения деформаций участков, предполагая их упругими Отсюда получаем второе уравнение 12. Проверяем равновесие рамы в целом. Для этого убираем опорные связи и их действие заменяем внутренними силовыми факторами в сечениях. Значения этих факторов определяем по эпюрам
4.2. Матричный алгоритм метода перемещений Выведем формулу, выражающую алгоритм метода перемещений. Для этого будем использовать матричные соотношения предыдущего параграфа. Окончательный вектор моментов, если известен вектор перемещений Вектор перемещений определяем, решая систему канонических уравнений метода перемещений (4.28). Если подставить (4.28) в (4.29). то получим Подставляя сюда выражения (4.25) и (4.27), получим окончательно
4.2.1. Аналогия матричных алгоритмов метода сил и метода перемещений Сравним формулы для векторов окончательных эпюр моментов при расчёте по методу перемещениий (4.31) и при расчёте по методу сил (3.16) Структура обеих формул совершенно одинаковая - она отражает общую логику рассуждений при расчёте статически неопределимых систем: 1. Заданная система разделяется на участки. Начало и конец каждого участка отмечается сечением со своим номером. Для каждого участка назначается правило знаков для ординат эпюр моментов в отмеченных сечениях. 2. Выбирается основная система - для каждого метода своя. 3. Вводятся векторы неизвестных ( 4. В основной системе формируется матрица влияния моментов 5. В основной системе строится эпюра от нагрузки 6. Только в методе перемещений строится эпюра моментов 7. Для каждого участка формируется матрица податливости 8. Там, где указан индекс f, в соответствующей матрице учитывается влияние стрелки f. Далее расчёт проводится совершенно одинаково, используя действия матричной алгебры.
4.2.2. Программа SETAPR.EXE для метода перемещений. Пример. Программа SETAPR поддерживает возможность расчёта статически неопределимых систем не только методом сил, как описано в п. 3.1.3,но и методом перемещений. Совместить два метода в одной программе удалось, используя аналогию, указанную в п. 4.2.1. Подготовка исходных данных проводится так же, как это указано в п. 3.1.3, но при расчёте по методу перемещений в файле APR2.DAT в режиме EDIT кроме пяти массивов, смысл которых описан в п. 3.1.3, записывается шестой массив - элементы вектора грузовых реакций Таким образом, по существу при расчёте по методу перемещений программа выполняет алгоритм, учитывающий, что вектор
Следует также отметить, что при программировании формул (3.16) и (4.32) в памяти ПЭВМ не хранится матрица В всей системы, а для каждого участка производится перемножение трёх сомножителей в формуле Мора и затем суммирование по всем участкам системы. Такой приём позволяет избежать засорения оперативной памяти большим числом нулей, находящихся в матрице В.
ПРИМЕР № 1. Проведём расчёт рамы с помощью программы SETAPR.EXE. В файле APR1.DAT записываем следующую исходную информацию: name 0 0 0 -1 0.666666 -1.333333 0.666666 -0.333333 -0.333333 0 0 0 -0.666666 0.666666 0.166666 -0.166666 В файле APR2.DAT в первой строке записываем массив коэффициентов податливостей участков по формуле 0.5 0.5 0.5 1 2 2 2 2 2 33.75 0 0 0 -33.75 0 0 0 0 33.75 90 Запускаем программу, хранящуюся в файле setapr.exe. В процессе работы происходит следующий диалог: степень статической неопределимости - в ответ вводится 2; число участков системы - в ответ вводится число 4; число сечений - в ответ вводится число 8; число участков с равномерно распределенной нагрузкой - вводится число 1; число участков с двумя расчетными сечениями - вводится 4; число участков с одним расчетным сечением - вводится 0; признак метода расчета (метод сил- 0; метод перемещений - 1) - вводится 1. После работы программа открывает в каталоге C:\X_Z файл name.res, в который выводятся искомые векторы Вектор перемещений вычислен с точностью до мн<
|
|||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.185.143 (0.019 с.) |

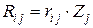 (4.5)
(4.5) , запишем систему канонических уравнений для определения
, запишем систему канонических уравнений для определения 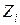
 (4.6)
(4.6)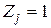 , то по (4.5)
, то по (4.5)  , то есть
, то есть  - реакция в связи основной системы с номером i от перемещения
- реакция в связи основной системы с номером i от перемещения 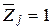 . В дальнейшем
. В дальнейшем  будем называть единичными реакциями. Свободные члены системы уравнений
будем называть единичными реакциями. Свободные члены системы уравнений 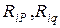 представляют собой реакции в связях основной системы от заданной нагрузки. Их часто называют грузовыми реакциями. Все реакции
представляют собой реакции в связях основной системы от заданной нагрузки. Их часто называют грузовыми реакциями. Все реакции 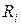 положительны, если направлены в ту же сторону, что и соответствующее перемещение
положительны, если направлены в ту же сторону, что и соответствующее перемещение  и
и  Эпюры изгибающих моментов в таких балках построим с помощью готового решения (см. п 3.3, пример № 6). Превратим нашу балку в двух состояниях в балку с шарнирами у плавающих заделок, приложив к сечениям справа и слева от шарниров соответствующие изгибающие моменты Будем считать состояние i действительным, а j - состоянием, перемещения в котором являются возможными для состояния i.
Эпюры изгибающих моментов в таких балках построим с помощью готового решения (см. п 3.3, пример № 6). Превратим нашу балку в двух состояниях в балку с шарнирами у плавающих заделок, приложив к сечениям справа и слева от шарниров соответствующие изгибающие моменты Будем считать состояние i действительным, а j - состоянием, перемещения в котором являются возможными для состояния i.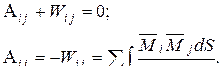
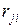 :
:
 Отсюда,
Отсюда, , (4.7)
, (4.7)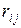 при неизвестных
при неизвестных  в системе (4.6) относительно членов
в системе (4.6) относительно членов  на главной диагонали.
на главной диагонали.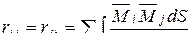 . (4.8)
. (4.8)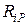 рассмотрим основную систему метода перемещений для рамы
рассмотрим основную систему метода перемещений для рамы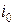 , а затем к той же системе приложим все реакции в р -ом состоянии (
, а затем к той же системе приложим все реакции в р -ом состоянии (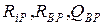 ) и силу Р - получится состояние
) и силу Р - получится состояние 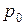 . Обе системы имеют одинаковые опорные закрепления и, следовательно, перемещения в любой из этих систем являются возможными для другой. По теореме о взаимности работ
. Обе системы имеют одинаковые опорные закрепления и, следовательно, перемещения в любой из этих систем являются возможными для другой. По теореме о взаимности работ , (4.9)
, (4.9) - работа сил в состоянии
- работа сил в состоянии  :
: ; (4.10)
; (4.10)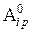 - работа сил в состоянии
- работа сил в состоянии  на возможных для него перемещениях в состоянии
на возможных для него перемещениях в состоянии 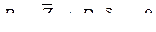 . (4.12)
. (4.12)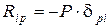 , (4.13)
, (4.13) 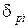 - перемещение по направлению Р, вызываемое поворотом узла
- перемещение по направлению Р, вызываемое поворотом узла 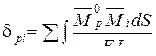 . (4.14)
. (4.14) -ординаты эпюры моментов в основной системе метода перемещений от причины, вызывающей
-ординаты эпюры моментов в основной системе метода перемещений от причины, вызывающей  ,- от поворота
,- от поворота  - ординаты эпюры изгибающих моментов в системе без плавающих заделок от силы
- ординаты эпюры изгибающих моментов в системе без плавающих заделок от силы  , приложенной по направлению искомого перемещения (совпадает с направлением силы Р, от которой мы ищем реакцию в основной системе метода перемещений).
, приложенной по направлению искомого перемещения (совпадает с направлением силы Р, от которой мы ищем реакцию в основной системе метода перемещений). , то есть ординаты эпюры изгибающих моментов в системе без связей метода перемещений от заданной силы Р, и, подставляя (4.14) в (4.13), окончательно будем иметь
, то есть ординаты эпюры изгибающих моментов в системе без связей метода перемещений от заданной силы Р, и, подставляя (4.14) в (4.13), окончательно будем иметь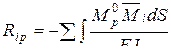 . (4.15)
. (4.15)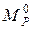 . В этой системе должно быть одно ограничение - в ней должна отсутствовать связь, препятствующая перемещению
. В этой системе должно быть одно ограничение - в ней должна отсутствовать связь, препятствующая перемещению 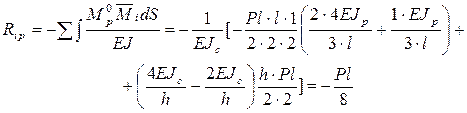 ,
,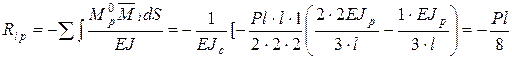 .
.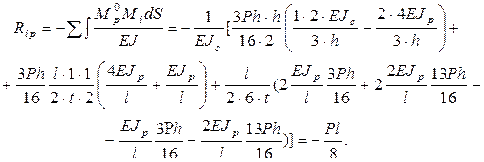 ,
, .
.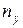 =1 - один жёсткий узел (не считая опорных).
=1 - один жёсткий узел (не считая опорных). врезаем во все узлы (включая и опорные) полные шарниры и считаем степень подвижности (4.2) W = 2 Y-C. Y =2 - число изолированных узлов, С =4 - число связей, W =2*2-4 =0.
врезаем во все узлы (включая и опорные) полные шарниры и считаем степень подвижности (4.2) W = 2 Y-C. Y =2 - число изолированных узлов, С =4 - число связей, W =2*2-4 =0.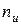 =1. Итак, степень кинематической неопределимости равна
=1. Итак, степень кинематической неопределимости равна 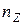 =2. Неизвестные метода перемещений: угол поворота
=2. Неизвестные метода перемещений: угол поворота  и линейное перемещение диска ВС на величину
и линейное перемещение диска ВС на величину 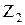 .
.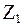 и
и 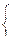
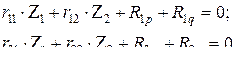
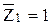 (чёрточка указывает, что
(чёрточка указывает, что  не равно
не равно 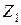 , а только совпадает с
, а только совпадает с  отсутствует. Эпюра моментов
отсутствует. Эпюра моментов  в каждом из стержней основной системы строится по готовым решениям для балок I и II типов (см. п. 3.3) в соответствии с видом изогнутой оси - ординаты откладываются в сторону растянутого волокна.
в каждом из стержней основной системы строится по готовым решениям для балок I и II типов (см. п. 3.3) в соответствии с видом изогнутой оси - ординаты откладываются в сторону растянутого волокна.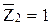 , а плавающая заделка не поворачивается. Эпюра моментов
, а плавающая заделка не поворачивается. Эпюра моментов 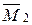 так же строится с помощью шаблонов (см. п. 3.3) в соответствии с видом изогнутой оси каждой балки I и II типов.
так же строится с помощью шаблонов (см. п. 3.3) в соответствии с видом изогнутой оси каждой балки I и II типов. так же строится с помощью готовых решений (см. п. 3.3).
так же строится с помощью готовых решений (см. п. 3.3). - это реакция в плавающей заделке по направлению перемещения
- это реакция в плавающей заделке по направлению перемещения  .
. .
.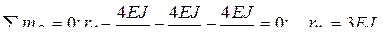
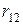 - это реакция в плавающей заделке от перемещения
- это реакция в плавающей заделке от перемещения 
 - это реакция в связи 2 от перемещения
- это реакция в связи 2 от перемещения 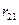 в опорной связи и поперечные силы в сечениях стержней, примыкающих к ригелю. Положительное направление
в опорной связи и поперечные силы в сечениях стержней, примыкающих к ригелю. Положительное направление  . В сечениях стоек показываем поперечные силы, величина и направление которых соответствует эпюре
. В сечениях стоек показываем поперечные силы, величина и направление которых соответствует эпюре 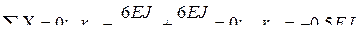
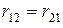 , что соответствует (4.7). Интересно, что
, что соответствует (4.7). Интересно, что 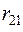 совершенно различные физические величины:
совершенно различные физические величины: 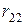 - это реакция в связи 2 от перемещения
- это реакция в связи 2 от перемещения 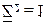 в состоянии 2. Поэтому выполняем ту же процедуру, что и при вычислении
в состоянии 2. Поэтому выполняем ту же процедуру, что и при вычислении 
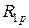 в плавающей заделке №1 равен нулю, так как сила Р приложена к центру узла. Реактивный момент
в плавающей заделке №1 равен нулю, так как сила Р приложена к центру узла. Реактивный момент 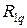 определяем, вырезая узел с плавающей заделкой в третьем грузовом состоянии. Составляем уравнение равновесия
определяем, вырезая узел с плавающей заделкой в третьем грузовом состоянии. Составляем уравнение равновесия кНм.
кНм.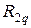 =0, а для вычисления
=0, а для вычисления 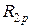 , рассмотрим равновесие ригеля в третьем состоянии
, рассмотрим равновесие ригеля в третьем состоянии кН.
кН. определяются по формуле
определяются по формуле 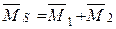 . Кроме того, построим из заданной статически определимую геометрически неизменяемую систему и определим в ней изгибающие моменты от заданной нагрузки - ординаты эпюры
. Кроме того, построим из заданной статически определимую геометрически неизменяемую систему и определим в ней изгибающие моменты от заданной нагрузки - ординаты эпюры  (4.17)
(4.17)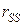 с помощью перемножения эпюры
с помощью перемножения эпюры 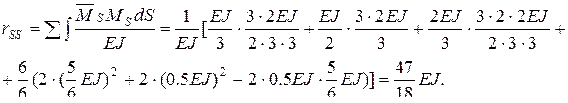

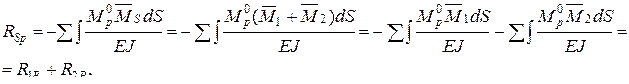 где индекс Р объединяет действие и нагрузки q и сосредоточенной силы. Таким образом, если вычислить
где индекс Р объединяет действие и нагрузки q и сосредоточенной силы. Таким образом, если вычислить 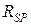 с помощью перемножения под интегралом эпюры
с помощью перемножения под интегралом эпюры 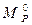 , то результат будет равен сумме “грузовых” коэффициентов системы уравнений. Для нашей системы получим
, то результат будет равен сумме “грузовых” коэффициентов системы уравнений. Для нашей системы получим 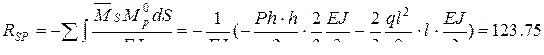 .
.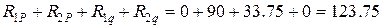 .
.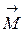 , элементами которого являются ординаты окончательной эпюры моментов в расчётных сечениях и величины стрелок на участках, где действует равномерно распределённая нагрузка. Если в системе H сечений и одна стрелка, то
, элементами которого являются ординаты окончательной эпюры моментов в расчётных сечениях и величины стрелок на участках, где действует равномерно распределённая нагрузка. Если в системе H сечений и одна стрелка, то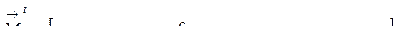 . (4.18)
. (4.18) . (4.19)
. (4.19) , (4.20)
, (4.20) - матрица единичных реакций или матрица жёсткости
- матрица единичных реакций или матрица жёсткости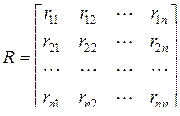 , (4.21)
, (4.21) - вектор грузовых или свободных членов
- вектор грузовых или свободных членов (4.22)
(4.22)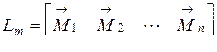 (4.23)
(4.23) . Для нашего примера
. Для нашего примера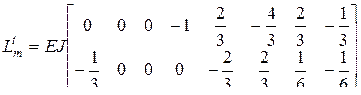 ;
; .
. .
.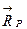 .
. и для единичных реакций (4.8)
и для единичных реакций (4.8)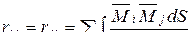 , убеждаемся в их полном структурном совпадении (при этом изгибающие моменты в обеих формулах возникают в разных основных системах). Поэтому
, убеждаемся в их полном структурном совпадении (при этом изгибающие моменты в обеих формулах возникают в разных основных системах). Поэтому 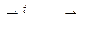 , (4.24)
, (4.24) и
и  - векторы эпюр моментов в единичных состояниях (при
- векторы эпюр моментов в единичных состояниях (при 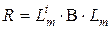 (4.25)
(4.25)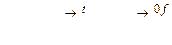 (4.26)
(4.26) (4.27)
(4.27)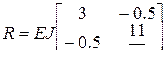 ;
; 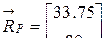 .
.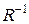
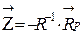 (4.28)
(4.28)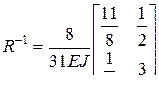 .
.
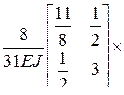
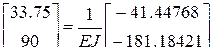 .
.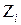 и от нагрузки в основной системе. Ординаты эпюр от
и от нагрузки в основной системе. Ординаты эпюр от 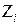 . Вся процедура умножения на
. Вся процедура умножения на 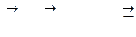 (4.29)
(4.29) Отметим, что так же как в методе сил, абсолютная величина жёсткости сечения не влияет на значения ординат окончательной эпюры моментов - играют роль отношения жёсткости каждого сечения к модульной жёсткости, за которую можно принять любое значение.
Отметим, что так же как в методе сил, абсолютная величина жёсткости сечения не влияет на значения ординат окончательной эпюры моментов - играют роль отношения жёсткости каждого сечения к модульной жёсткости, за которую можно принять любое значение. -7.6974 - 57.8283 + 65.5227 = 0. Условие равновесия узла удовлетворяется.
-7.6974 - 57.8283 + 65.5227 = 0. Условие равновесия узла удовлетворяется.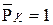 и построим эпюру моментов
и построим эпюру моментов 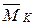 . Эту эпюру будем использовать для определения горизонтального перемещения точки К, которое заведомо должно быть равно нулю, так как в этом месте находится опора К.
. Эту эпюру будем использовать для определения горизонтального перемещения точки К, которое заведомо должно быть равно нулю, так как в этом месте находится опора К.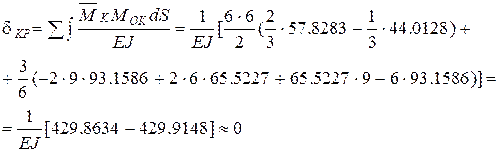
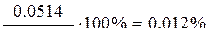 . Точность вполне достаточная, следовательно, окончательная эпюра изгибающих моментов построена верно.
. Точность вполне достаточная, следовательно, окончательная эпюра изгибающих моментов построена верно.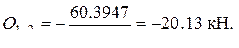
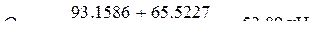
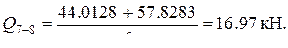

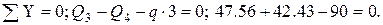
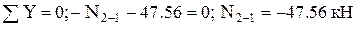

 и
и 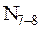 остаётся одно уравнение
остаётся одно уравнение 
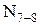 -
- 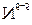 - 42.43 = 0.
- 42.43 = 0.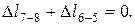
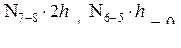
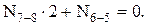 Решая совместно это уравнение с уравнением равновесия, получим
Решая совместно это уравнение с уравнением равновесия, получим  .
.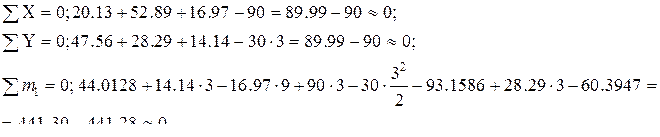 Погрешность
Погрешность  Рама рассчитана верно.
Рама рассчитана верно. , получаем по (4.29). При этом стрелки участков с криволинейным очертанием эпюр будем учитывать отдельно.
, получаем по (4.29). При этом стрелки участков с криволинейным очертанием эпюр будем учитывать отдельно.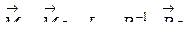 . (4.30)
. (4.30)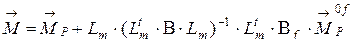 (4.31)
(4.31)

 - в методе сил,
- в методе сил,  - в методе перемещений).
- в методе перемещений). путём построения единичных эпюр - эпюр моментов от единичных факторов, совпадающих по направлению с неизвестными.
путём построения единичных эпюр - эпюр моментов от единичных факторов, совпадающих по направлению с неизвестными. 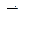 .
.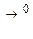 от нагрузки в статически определимой системе, полученной из заданной путём отбрасывания лишних связей.
от нагрузки в статически определимой системе, полученной из заданной путём отбрасывания лишних связей.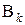 , которые затем образуют матрицу податливости всей системы B.
, которые затем образуют матрицу податливости всей системы B. в основной системе метода перемещений, которые студент должен определить статическим способом, указанным в п. 4.1.4.
в основной системе метода перемещений, которые студент должен определить статическим способом, указанным в п. 4.1.4. . (4.32)
. (4.32)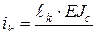 и далее, как указано (п. 3.1.3):
и далее, как указано (п. 3.1.3):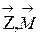
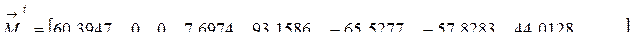 ;
;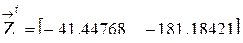 .
.


