
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет статически неопределимых стержневыхСодержание книги
Поиск на нашем сайте
СИСТЕМ С ПОМОЩЬЮ ПЭВМ МЕТОДОМ СИЛ 3.1. Метод сил для расчета статически неопределимых плоских стержневых систем 3.1.1 Степень статической неопределимости. Основная система Статически неопределимыми системами называются системы, для расчета которых недостаточно только уравнений статики. Недостающие уравнения составляются путем рассмотрения упругих деформаций системы. Количество этих уравнений n называется степенью статической неопределимости. Рассмотрим раму в виде замкнутого контура. Проведя разрез в любом месте К с целью вычисления внутренних силовых факторов (изгибающего момента, поперечной и нормальной сил), мы столкнемся с необходимостью предварительно найти реакции в опорных закреплениях. Общее число реакций -6, а уравнений равновесия для плоской системы -3. Недостает трех уравнений для определения всех реакций и далее всех внутренних силовых факторов. Тот же результат будет в случае замкнутого контура. В этом случае реакции в опорных закреплениях можно определить из уравнений статики, но, сделав разрез в любом месте, мы с помощью уравнений равновесия сможем доказать только равенство внутренних силовых факторов на соседних “берегах” разреза, но не сможем определить их величину. Следовательно, рама в виде замкнутого контура трижды статически неопределима. Посмотрим теперь, что изменится, если схема рамы будет содержать простой шарнир
При этом степень статической неопределимости будет уже равна двум - на единицу меньше. Увеличение числа простых шарниров будет уменьшать число n. В конце концов, получим статически определимую систему. Включение в контур более трех шарниров превращает систему в изменяемую. Итак, включение в замкнутый контур простого шарнира снижает степень статической неопределимости на единицу. Представим теперь, что в плоской стержневой системе можно выделить К замкнутых контуров и Ш простых шарниров. Тогда степень статической неопределимости можно вычислить по формуле n = 3 К-Ш (3.1)
ПРИМЕР № 1 Подсчитать степень статической неопределимости для схемы рамы Количество замкнутых контуров К=6. Количество простых шарниров Ш=7. Степень статической неопределимости n = 3*6-7 = 11. Для расчета n раз статически неопределимой системы методом сил она преобразуется в другую систему путем устранения n связей. Полученная система должна быть геометрически неизменяемой и, как правило, статически определимой. Такая система называется основной системой. Основная система находится под действием заданной нагрузки и неизвестных усилий и моментов, действующих в устраненных связях. Эти неизвестные обозначаются
3.1.2 Матричный алгоритм метода сил Дополнительные уравнения по этому методу выражают условия, что основная система по направлению отброшенных связей должна деформироваться точно так же, как заданная. Таких условий будет n - по числу отброшенных связей. Таким образом, для любой основной системы можно составить n уравнений деформации, из которых затем определить n неизвестных Алгоритм расчета статически неопределимой системы методом сил в матричной форме проследим на примере конкретной рамы. При этом формулы будут приводится для общего случая. 1. Разбиваем раму на участки, работающие на изгиб. Начало и конец каждого участка отмечаем сечениями с индивидуальным номером. Для каждого участка принимаем свое правило знаков для ординат эпюры моментов, отложенных в сторону растянутого волокна. Обозначим количество участков системы r = 5, количество сечений H = 10. Конечной целью расчета является вычисление моментов в отмеченных сечениях, образующих вектор 2. Подсчет степени статической неопределимости. Количество замкнутых контуров (включая опорные) К=4. Количество простых шарниров (в сечениях 1 и 10 - шарниры сложные и содержат по два простых) Ш=10. По формуле (3.1) получим n =3*4-10=2. Рама два раза статически неопределимая. 3. Выбор основной системы. Каждому варианту основной системы соответствует свой объём перерабатываемой числовой информации. Практика расчетов показывает, что наиболее устойчивые результаты получаются для основных систем, деформированный вид которых близок к виду деформации заданной системы. Этому условию удовлетворяет основная система. Она представляет собой трехшарнирную раму АВСТ и опирающийся на нее диск в виде балки СД с шарниром в сечении 7 и связью в сечении 8, не проходящей через этот шарнир - система геометрически неизменяемая и статически определимая. Основная система находится под действием заданной нагрузки и неизвестных моментов, образующих вектор неизвестных Для нашей системы n =2. 4. Составление системы уравнений деформации. Первое уравнение выражает тот факт, что в заданной системе сечения 4 и 5 поворачиваются на один и тот же угол, то есть разность поворотов сечений 4 и 5 должна быть равна нулю. В общем случае эта разность зависит от Второе уравнение выражает тот факт, что в заданной системе разность углов поворота сечений 6 и 7 должна быть равна нулю (сечение 6 поворачивается на тот же угол, что и сечение 7, так как узел 6-7-9 жесткий). Таким образом, Все рассматриваемые перемещения малы по сравнению с размерами системы, поэтому справедлив принцип независимости действия сил. Каждое перемещение от нескольких факторов равно сумме соответствующих перемещений от каждого фактора, приложенного отдельно: Далее учтем, что перемещения от каждого неизвестного где Если Таким образом, получаем систему которая называется канонической системой уравнений метода сил. Какова бы ни была фактически два раза статически неопределимая система, уравнения для определения неизвестных будут иметь тот же вид. Первые индексы при коэффициентах имеют индекс соответствующий номеру уравнения. Вторые индексы увеличиваются от 1 до n (в нашем случае n =2). Если для n раз статически неопределимой системы ввести матрицу, компоненты которой представляют собой коэффициенты при неизвестных и матрицу свободных членов (перемещений от заданной нагрузки) то систему канонических уравнений метода сил можно записать в виде матричного уравнения Здесь индексом Р обозначена любая внешняя нагрузка. 5. Определение коэффициентов канонических уравнений. Все компоненты матриц (3.4) и (3.5) представляют собой перемещения. Поэтому для их определения можно применить формулу Мора в виде (2.28). Таким образом, В формулах (3.7) и (3.8) указаны векторы эпюр внутренних силовых факторов от каждого В нашем случае это эпюры Записываем эпюры от единичных сил в виде матриц-столбцов и формируем из них матрицу влияния моментов в основной системе В нашем случае Записываем эпюру от нагрузки в виде вектора в котором между сечениями 7 и 8 учтена стрелка f = 45. Если в формулах (3.7) и (3.8) вместо первых сомножителей поставить транспонированную матрицу Индекс f у матрицы податливости системы В означает, что в векторе Если на место третьего сомножителя в (3.10) поставить матрицу 6. Решение системы канонических уравнений. Систему уравнений можно решить с помощью обратной матрицы Далее учтем, что произведение исходной матрицы на обратную (в любой последовательности) дает единичную, которая, будучи умноженной на любую другую, последнюю не изменяет. Таким образом, решение системы канонических уравнений метода сил имеет следующий вид 7. Вычисление ординат окончательной эпюры внутренних силовых факторов (3.2). Изгибающий момент в любом сечении статически неопределимой системы можно вычислить, используя принцип независимости действия сил, суммируя в этом сечении моменты от нагрузки и усилий в отброшенных связях Эта процедура для всей системы описывается следующей формулой Подставим в (3.14) выражения (3.11) и (3.12), а затем все это в (3.15), получим В этом алгоритме присутствуют три матрицы: матрица Для систем, где нужно учитывать как деформации изгиба так и растяжения-сжатия, в формуле (3.16) нужно использовать векторы, имеющие структуру (2.33)
3.1.3 Программа SETAPR.EXE. Примеры Процедура вычисления вектора внутренних усилий в отмеченных сечениях статически неопределимой системы (3.17) составила алгоритм программы, находящейся в файле SETAPR.EXE и написанной на языке программирования Turbo Pascal 6.0. Для работы программы должны быть предварительно заполнены файлы APR1.DAT и APR2.DAT, находящиеся в каталоге C:\X_Z. Порядок работы с файлами описан в п.1.3. В файле APR1.DAT в режиме EDIT в первой строке записывается имя или фамилия студента латинскими буквами, а в последующих строках - транспонированные векторы эпюр внутренних усилий в основной системе метода сил от единичных силовых факторов В файле APR2.DAT в режиме EDIT записывается по группам следующая информация: 1) Массив коэффициентов 2) Массив чисел, каждое из которых соответствует числу расчетных сечений на участке системы (массив состоящий из 2 и 1); 3) Массив номеров участков, где действует равномерно распределенная нагрузка; 4) Массив значений стрелок эпюр f от действия раномерно распределенной нагрузки на соответствующих участках; 5) Транспонированный вектор эпюры внутренних усилий от нагрузки, вызывающей перемещения (без учета стрелок эпюр). При записи исходной информации в файлы каждую группу целесообразно начинать с новой строки. При этом следует быть внимательным: эти файлы имеют текстовый тип, поддерживаемый языком Pascal, и каждая запись числа должна отделяться одним пробелом, а первое число в строке пишется без предшествующего пробела. После того, как файлы исходных данных подготовлены, запускается программа в файле SETAPR.EXE нажатием клавиши ENTER. Программа запрашивает о готовности исходной информации. Если файлы готовы, то нужно нажать клавишу Y, если нет, то N. При нажатии N программа выводит на экран структуру информации, записываемой в указанных файлах. После нажатия ENTER происходит возврат в окна Нортона. Если нажат ответ Y, то программа запрашивает информацию о размерности в диалоговом режиме следующим образом: степень статической неопределимости - в ответ вводится n; число участков системы - в ответ вводится число r; число сечений - в ответ вводится число h; число участков с равномерно распределенной нагрузкой - вводится число st; число участков с двумя расчетными сечениями - вводится С; число участков с одним расчетным сечением - вводится D; признак метода расчета (метод сил- 0; метод перемещений - 1) - вводится 0. После работы программа открывает в каталоге C:\X_Z файл....RES, в который выводятся искомые векторы
ПРИМЕР №2 Закончим расчет рамы. Необходимые эпюры. В файле APR1.DAT записываем следующую исходную информацию: name 0 0.5 0.5 1 1 1 0 0 1 0 0 0 0 0 0 1 1 0 0 0 В файле APR2.DAT в первой строке записываем массив коэффициентов податливостей участков по формуле 0.25 0.25 0.5 0.5 0.5 2 2 2 2 2 4 45 0 30 30 0 0 -60 0 0 -60 0 Запускаем программу, хранящуюся в файле setapr.exe. В процессе работы происходит следующий диалог: степень статической неопределимости - в ответ вводится 2; число участков системы - в ответ вводится число 5; число сечений - в ответ вводится число 10; число участков с равномерно распределенной нагрузкой - вводится число 1; число участков с двумя расчетными сечениями - вводится 5; число участков с одним расчетным сечением - вводится 0; признак метода расчета (метод сил- 0; метод перемещений - 1) - вводится 0. После работы программа открывает в каталоге C:\X_Z файл name.res, в который выводятся искомые векторы Окончательная эпюра моментов. Проверку правильности построения окончательной эпюры моментов проведем двумя способами - статическим и деформационным. Первый способ состоит в проверке равновесия узлов рамы. Вырежем узлы 4-5 и 6-7-9 и покажем действующие в сечениях изгибающие моменты. Вращение узлов должно отсутствовать, то есть сумма приложенных к узлу моментов должна быть равна нулю. В нашем случае проверка удовлетворяется. Второй способ (деформационная проверка) состоит в определении перемещения, величина которого заранее известна (например, должна быть равна нулю). Перемещение определяется, как правило, по формуле Мора. За единичное состояние можно принять состояние основной системы под действием какого-либо Это можно сделать с помощью программы SETPEREM.EXE или по обычной формуле Мора с применением правила Верещагина. Воспользуемся последним способом. При выполнении лабораторных работ это целесообразно, так как студент должен знать классические формулы.
Проверка удовлетворяется. Таким образом, ординаты эпюры моментов в заданной статически неопределимой системе найдены верно. В этих случаях говорят, что статическая неопределимость “раскрыта”. После этого, остальные внутренние силовые факторы (Q и N) можно найти, используя уравнения равновесия частей рамы. При построении эпюры Q можно на каждом участке применять дифференциальную зависимость При этом, если эпюра моментов очерчена прямой линией и отложена в сторону растянутого волокна, то значение Q по модулю равно тангенсу угла наклона линии эпюры моментов к оси стержня | Q |= а знак определяется следующим образом: если ось стержня поворачивается при совмещении с эпюрой по часовой стрелке, то Q >0, если против, то Q <0. Участок 1-2. Q=45/1.5=30 kH. Участок 3-4. Q=-(45-30)/1.5=-10 kH. Участок 5-6. Q=-(45+30)/6=-12.2 kH. Участок 9-10. Q=30/3=10 kH. Там, где эпюра моментов криволинейная (участок 7-8), поступим следующим образом. Вырежем этот участок из состава рамы и рассмотрим его равновесие отдельно. Покажем на оставшейся части внешнюю нагрузку, моменты в сечениях и неизвестные поперечные силы Q в положительном направлении - так, что они стремятся вращать стержень по часовой стрелке относительно ближайшей к сечению точке на оси стержня.
Проведем разрез на расстоянии z отсечения 7 и рассмотрим равновесие левой оставшейся части.
Эпюра Q на участке, где действует равномерно распределённая нагрузка, всегда очерчивается прямой линией, наклонной к оси стержня и соединяющей ординаты по краям участка. На участке 7-8 поперечная сила меняет знак - в этом месте функция изгибающего момента имеет экстремум.
Точка с экстремальным значением изгибающего момента находится правее середины участка 7-8 При построении эпюры продольных (нормальных) сил следует учесть, что если внешняя нагрузка действует перпендикулярно оси участка, к которому она приложена, то N =const по длине участка. Значения продольных сил в сечениях рамы определяют из условий равновесия её узлов. Вырежем узлы 4-5 и 6-7-9, покажем действующие на них в сечениях известные поперечные силы и неизвестные продольные Узел 4-5
Узел 6-7-9
Теперь необходимо сделать проверку равновесия рамы в целом. Для этого освободим раму от опор и покажем внутренние силовые факторы в опорных сечениях. Под действием этих сил и заданной нагрузки рама должна находиться в равновесии.
Условия удовлетворяются. Следовательно, все эпюры построены верно. ПРИМЕР № 3 Построить эпюры M и N в статически неопределимой системе. Система представлена статически неопределимой балкой с упруго податливой опорой. Количество замкнутых контуров К =1, количество простых шарниров Ш =2. Степень статической неопределимости n =3* K-Ш =1.. Отбрасываем упругую опору, прикладываем действующее в ней неизвестное усилие
Определяем коэффициенты податливостей участков, умноженных на модульную жесткость (в этом расчете - жесткость сечения балки при изгибе):
В файле c:\X_Z\apr1.dat записываем фамилию студента и с новой строки - вектор внутренних усилий от Petrov 4 0 -1 В файле c:\X_Z\apr2.dat, учитывая отсутствие равномерно распределённой нагрузки, записываем: 0.666666 32 2 1 -4 0 0 Запускаем программу, хранящуюся в файле setapr.exe. В процессе работы происходит следующий диалог: степень статической неопределимости - в ответ вводится 1; число участков системы - в ответ вводится число 2; число сечений - в ответ вводится число 3; число участков с равномерно распределенной нагрузкой - вводится число 0; число участков с двумя расчетными сечениями - вводится 1; число участков с одним расчетным сечением - вводится 1; признак метода расчета (метод сил- 0; метод перемещений - 1) - вводится 0. После работы программа открывает в каталоге C:\X_Z файл petrov.res, в который выводятся искомые векторы S(1)=-3.00000E+00 X=-2.50000E-01 S(2)=0.00000E+00 S(3)=-2.50000E-01 Этот результат показывает влияние податливости правой опоры на распределение усилий: если опора абсолютно жёсткая, то балка не изгибается, а действие внешней нагрузки воспринимается только сжатием опорного стержня на величину силы; если опора отсутствует, то балка изгибается как консольная - при этом момент в сечении 1 равен
3.2. Расчет статически неопределимых балок на подвижную нагрузку 3.2.1. Матрица влияния усилий в неразрезной балке В пункте 2.5.1 показан способ построения линий влияния усилий в многопролетных статически определимых балках с помощью матрицы влияния моментов где Н - количество точек на оси балки, где поочередно действует сила Таким образом, в каждом векторе Как указывалось в п. 2.5.1, если в матрице Для расчета балки на каждое единичное воздействие применим метод сил по алгоритму (3.17). Степень статической неопределимости равна числу промежуточных опор n. Основную систему образуем из заданной путем удаления над каждой промежуточной опорой связи, воспринимающей изгибающий момент, и введения неизвестных В основной системе строим эпюры изгибающих моментов и усилий в упругих опорах от
Для вычисления вектора усилий в заданной статически неопределимой балке
3.2.2. Программа для расчета неразрезных балок BALSET1.EXE Процедура вычисления вектора изгибающих моментов в отмеченных сечениях и определения опорных реакций в упругих опорах статически неопределимой балки (3.21) составила алгоритм программы, находящейся в файле BALSET1.EXE и написанной на языке программирования Turbo Pascal 6.0. Для работы программы должны быть предварительно заполнены файлы C:\INF\apr1.dat и C:\INF\apr2.dat, находящиеся в каталоге C:\INF. Порядок работы с файлами описан в п.1.3. В программе предполагается, что балка слева направо разделена на участки, работающие на изгиб. Начало и конец двух соседних участков имеют один номер. Каждая консоль, если она есть, представляет один участок, а каждый пролет балки разделяется на четыре участка равной длины. В файле APR1.DAT в режиме EDIT в первой строке записывается имя или фамилия студента латинскими буквами, а в последующих строках - транспонированные векторы В файле APR2.DAT в режиме EDIT записывается по группам следующая информация: 1) Массив коэффициентов 2) Массив коэффициентов 3) Массив номеров сечений балки, под которыми находятся опоры (слева направо); 4) Массив длин консолей, если они есть, и пролетов (слева направо) При записи исходной информации в файлы каждую группу целесообразно начинать с новой строки. При этом следует быть внимательным: эти файлы имеют текстовый тип, поддерживаемый языком Pascal, и каждая запись числа должна отделяться одним пробелом, а первое число в строке пишется без предшествующего пробела. После того, как файлы исходных данных подготовлены, запускается программа в файле BALSET1.EXE нажатием клавиши ENTER. Программа запрашивает о готовности исходной информации. Если файлы готовы, то нужно нажать клавишу Y, если нет, то N. При нажатии N программа выводит на экран структуру информации, записываемой в указанных файлах. После нажатия ENTER происходит возврат в окна Нортона. Если нажат ответ Y, то программа запрашивает информацию о размерности в диалоговом режиме следующим образом: степень статической неопределимости - в ответ вводится n; признак наличия консоли слева от первой опоры (да -1, нет - 0); признак наличия консоли справа от последней опоры (да -1, нет - 0); число участков, работающих на изгиб, - в ответ вводится число r; число опор многопролетной балки - в ответ вводится число nop; номер левой опоры пролета, в котором нужно построить огибающую эпюру М (для этого пролета вычисляются ординаты линий влияния М в двух опорных сечениях и трех сечениях в пролете) - в ответ вводится соответствующее число i. После работы программа открывает в каталоге C:\INF два файла результатов: файл c:\inf\...1.RES, в который выводятся искомые векторы
3.2.3. Пример расчета многопролетной балки на подвижную нагрузку Балка опирается на 5 опор и является 3 раза статически неопределимой системой n =3 K-Ш =3*5-12=3. В задании требуется построить огибающую эпюру
|
||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.235.66 (0.014 с.) |

 (простой шарнир - это шарнир, соединяющий два диска). Тогда, дополнительно к имеющимся трем уравнениям равновесия рамы в целом, можно составить ещё одно уравнение равенства нулю момента левых или правых сил относительно этого шарнира
(простой шарнир - это шарнир, соединяющий два диска). Тогда, дополнительно к имеющимся трем уравнениям равновесия рамы в целом, можно составить ещё одно уравнение равенства нулю момента левых или правых сил относительно этого шарнира
 .
. . Основная система метода сил может быть выбрана многими способами. Строго говоря, бесконечно многими. Например, если в каком-то месте стержня убрать связь, воспринимающую изгибающий момент (говорят “врезать шарнир”), и менять положение шарнира по длине стержня, то основная система будет каждый раз новая. Несколько вариантов основной системы для дважды статически неопределимой рамы.
. Основная система метода сил может быть выбрана многими способами. Строго говоря, бесконечно многими. Например, если в каком-то месте стержня убрать связь, воспринимающую изгибающий момент (говорят “врезать шарнир”), и менять положение шарнира по длине стержня, то основная система будет каждый раз новая. Несколько вариантов основной системы для дважды статически неопределимой рамы. .
.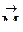 , имеющий в транспонированном виде структуру:
, имеющий в транспонированном виде структуру:
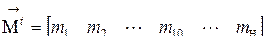 (3.2)
(3.2) (3.3)
(3.3)

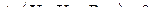

 .
. ,
, - коэффициент пропорциональности.
- коэффициент пропорциональности. , то
, то  ,то есть
,то есть  в основной системе. Здесь над обозначением неизвестного поставлена черточка для того, чтобы отметить, что это не действительное искомое усилие по направлению отброшенной связи, а силовой фактор, приложенный по тому же направлению но конкретной величины равной единице.
в основной системе. Здесь над обозначением неизвестного поставлена черточка для того, чтобы отметить, что это не действительное искомое усилие по направлению отброшенной связи, а силовой фактор, приложенный по тому же направлению но конкретной величины равной единице.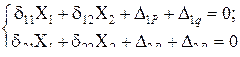 ,
,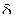 ,
,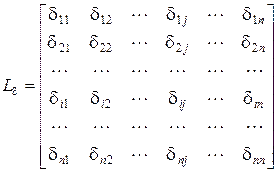 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6)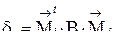 (3.7)
(3.7) (3.8)
(3.8)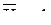 , приложенного в основной системе по направлению отброшенной связи с номером i, и от заданной внешней нагрузки Р.
, приложенного в основной системе по направлению отброшенной связи с номером i, и от заданной внешней нагрузки Р. и
и 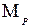
 (3.9)
(3.9) .
.  ,
, , то получим, как в (2.36), матрицы-столбцы перемещений по направлениям отброшенных связей в основной системе соответственно от
, то получим, как в (2.36), матрицы-столбцы перемещений по направлениям отброшенных связей в основной системе соответственно от 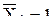 и заданной нагрузки Р
и заданной нагрузки Р (3.10)
(3.10) (3.11)
(3.11) учтены стрелки криволинейных эпюр.
учтены стрелки криволинейных эпюр. (3.12)
(3.12) , которую можно вычислить известными из курса математики способами (в том числе с помощью ЭВМ). Для этого умножим левую и правую стороны (3.6) на
, которую можно вычислить известными из курса математики способами (в том числе с помощью ЭВМ). Для этого умножим левую и правую стороны (3.6) на  (3.13)
(3.13) (3.14)
(3.14) на уже известную величину
на уже известную величину  . Таким образом, для сечения с номером k будем иметь
. Таким образом, для сечения с номером k будем иметь .
. (3.15)
(3.15)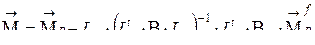 (3.16)
(3.16) представляет собой столбец эпюры от нагрузки и матрица податливости системы B, которая формируется по схеме (2.29). Все остальное выполняется по правилам матричной алгебры.
представляет собой столбец эпюры от нагрузки и матрица податливости системы B, которая формируется по схеме (2.29). Все остальное выполняется по правилам матричной алгебры. (3.17)
(3.17) , приложенных по направлениям отброшенных связей.
, приложенных по направлениям отброшенных связей. податливостей участков, то есть массив числовых множителей перед матрицами податливости участков в формулах (2.25), (2.27), (2.31), (2.34). Если участок работает на изгиб с двумя расчетными сечениями или с одним, то
податливостей участков, то есть массив числовых множителей перед матрицами податливости участков в формулах (2.25), (2.27), (2.31), (2.34). Если участок работает на изгиб с двумя расчетными сечениями или с одним, то  . Если участок работает на растяжение или сжатие, то
. Если участок работает на растяжение или сжатие, то  . За
. За  можно принять жесткость любого сечения. Дело в том, что при вычислении усилий в статически неопределимой системе методом сил достаточно знать только относительные жесткости сечений.
можно принять жесткость любого сечения. Дело в том, что при вычислении усилий в статически неопределимой системе методом сил достаточно знать только относительные жесткости сечений.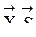 . Вместо многоточия название файла будет содержать имя или фамилию студента, введенную ранее в первую строку файла APR1.DAT. Содержимое файла-результата можно распечатать, нажав функциональную клавишу F9 в режиме EDIT.
. Вместо многоточия название файла будет содержать имя или фамилию студента, введенную ранее в первую строку файла APR1.DAT. Содержимое файла-результата можно распечатать, нажав функциональную клавишу F9 в режиме EDIT. и далее, как указано выше:
и далее, как указано выше: ;
;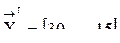 .
. , либо состояние, когда действуют все
, либо состояние, когда действуют все 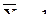 (суммарное единичное состояние). В результате перемножения эпюр M и
(суммарное единичное состояние). В результате перемножения эпюр M и  должен получиться 0, так как это свидетельствует о выполнении исходного условия о равенстве 0 перемещения по направлению отброшенной связи с номером i. Во всех случаях имеются в виду так называемые “обобщённые перемещения” - в нашем случае разность углов поворота сечений. Найдем разность углов поворота сечений 4 и 5.
должен получиться 0, так как это свидетельствует о выполнении исходного условия о равенстве 0 перемещения по направлению отброшенной связи с номером i. Во всех случаях имеются в виду так называемые “обобщённые перемещения” - в нашем случае разность углов поворота сечений. Найдем разность углов поворота сечений 4 и 5.
 Q (3.18)
Q (3.18) (3.19)
(3.19)


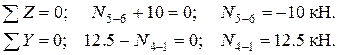


 и учитываем в расчете деформации изгиба и растяжения-сжатия. Размечаем расчетные сечения - №1 и №2 для изгиба и №3 для продольной деформации. Для каждого участка устанавливаем правило знаков. Эпюры внутренних силовых факторов от действия
и учитываем в расчете деформации изгиба и растяжения-сжатия. Размечаем расчетные сечения - №1 и №2 для изгиба и №3 для продольной деформации. Для каждого участка устанавливаем правило знаков. Эпюры внутренних силовых факторов от действия  и силы Р в основной системе. Записываем их в виде матриц-столбцов (векторов) со структурой по (2.33), где С =1; D =1.
и силы Р в основной системе. Записываем их в виде матриц-столбцов (векторов) со структурой по (2.33), где С =1; D =1.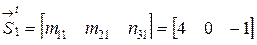 ;
; .
.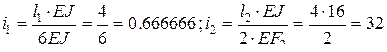 .
. кHм. Наша система при учете податливости опоры дает результат, находящийся между этими крайними случаями.
кHм. Наша система при учете податливости опоры дает результат, находящийся между этими крайними случаями. . Применим тот же способ при построении линий влияния изгибающих моментов и опорных реакций в многопролетных неразрезных балках на упруго податливых опорах. Жесткость сечений балки на изгиб может быть переменной. Для построения матрицы влияния внутренних усилий
. Применим тот же способ при построении линий влияния изгибающих моментов и опорных реакций в многопролетных неразрезных балках на упруго податливых опорах. Жесткость сечений балки на изгиб может быть переменной. Для построения матрицы влияния внутренних усилий  будем загружать балку единичной одиночной силой, действующей поочередно во всех заранее отмеченных сечениях, и каждый раз проводить расчет статически неопределимой балки с помощью программы BALSET1. Полученные результаты запишем в виде векторов, которые, будучи составленными вместе, образуют
будем загружать балку единичной одиночной силой, действующей поочередно во всех заранее отмеченных сечениях, и каждый раз проводить расчет статически неопределимой балки с помощью программы BALSET1. Полученные результаты запишем в виде векторов, которые, будучи составленными вместе, образуют 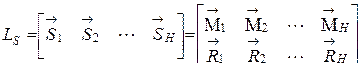 , (3.20)
, (3.20) .
. сначала перечисляются ординаты изгибающих моментов в сечениях балки
сначала перечисляются ординаты изгибающих моментов в сечениях балки  , а затем величины нормальных сил в опорных стержнях
, а затем величины нормальных сил в опорных стержнях  ,моделирующих упруго податливые опоры.
,моделирующих упруго податливые опоры. в неразрезной балке. Если выделенная строка соответствует продольному усилию в опорном стержне, то её ординаты представляют собой ординаты линии влияния этого усилия, то есть по существу это будут ординаты линии влияния опорной реакции, взятой с обратным знаком.
в неразрезной балке. Если выделенная строка соответствует продольному усилию в опорном стержне, то её ординаты представляют собой ординаты линии влияния этого усилия, то есть по существу это будут ординаты линии влияния опорной реакции, взятой с обратным знаком. =1 и образуем матрицу влияния усилий в основной системе
=1 и образуем матрицу влияния усилий в основной системе 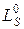 . Наша основная система отличается тем, что от каждого неизвестного моменты и опорные реакции возникают только в двух сопряжённых пролетах. Поэтому вектор
. Наша основная система отличается тем, что от каждого неизвестного моменты и опорные реакции возникают только в двух сопряжённых пролетах. Поэтому вектор  от
от  в матрице
в матрице  При каждом положении единичной силы в основной системе строится эпюра изгибающих моментов и усилий в опорных стержнях и записывается в виде вектора
При каждом положении единичной силы в основной системе строится эпюра изгибающих моментов и усилий в опорных стержнях и записывается в виде вектора  . Например для силы, стоящей в четверти пролета, этот вектор будет иметь вид
. Например для силы, стоящей в четверти пролета, этот вектор будет иметь вид
 (3.21)
(3.21) , приложенных по направлениям отброшенных связей, воспринимающих момент над промежуточными опорами.
, приложенных по направлениям отброшенных связей, воспринимающих момент над промежуточными опорами. податливостей участков балки, работающих на изгиб, то есть массив числовых множителей перед матрицами податливости участков в формуле (2.27). Для участка
податливостей участков балки, работающих на изгиб, то есть массив числовых множителей перед матрицами податливости участков в формуле (2.27). Для участка  , где
, где  - длина и жесткость сечения участка с номером k, а
- длина и жесткость сечения участка с номером k, а 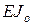 - жесткость любого сечения балки, принимаемой за модульную. Дело в том, что, как указывалось выше, при вычислении усилий в статически неопределимой системе методом сил достаточно знать только относительные жесткости сечений;
- жесткость любого сечения балки, принимаемой за модульную. Дело в том, что, как указывалось выше, при вычислении усилий в статически неопределимой системе методом сил достаточно знать только относительные жесткости сечений; , где
, где  - податливость упругой опоры, равная деформации опорного стержня, моделирующего эту опору, от действия вертикальной силы
- податливость упругой опоры, равная деформации опорного стержня, моделирующего эту опору, от действия вертикальной силы  . Если опора жесткая, то
. Если опора жесткая, то  .
.
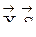 при каждом загружении единичной силой и файл c:\inf\...2.RES, в который выводятся ординаты пяти линий влияния моментов и линии влияния усилий во всех опорных стержнях. Вместо многоточия названия файлов будут содержать имя или фамилию студента, введенную ранее в первую строку файла APR1.DAT. Содержимое файлов-результатов можно распечатать, нажав функциональную клавишу F9 в режиме EDIT.
при каждом загружении единичной силой и файл c:\inf\...2.RES, в который выводятся ординаты пяти линий влияния моментов и линии влияния усилий во всех опорных стержнях. Вместо многоточия названия файлов будут содержать имя или фамилию студента, введенную ранее в первую строку файла APR1.DAT. Содержимое файлов-результатов можно распечатать, нажав функциональную клавишу F9 в режиме EDIT.


